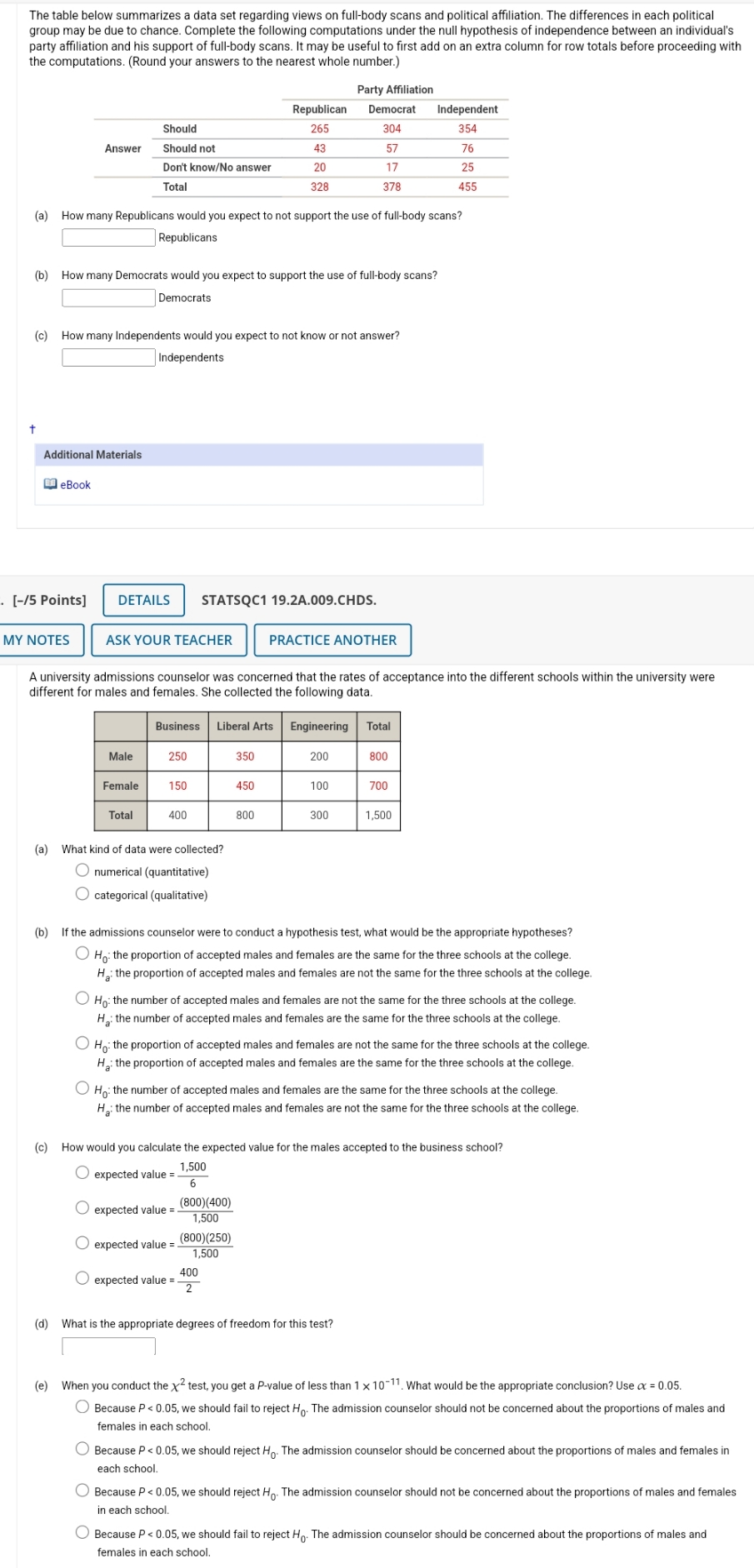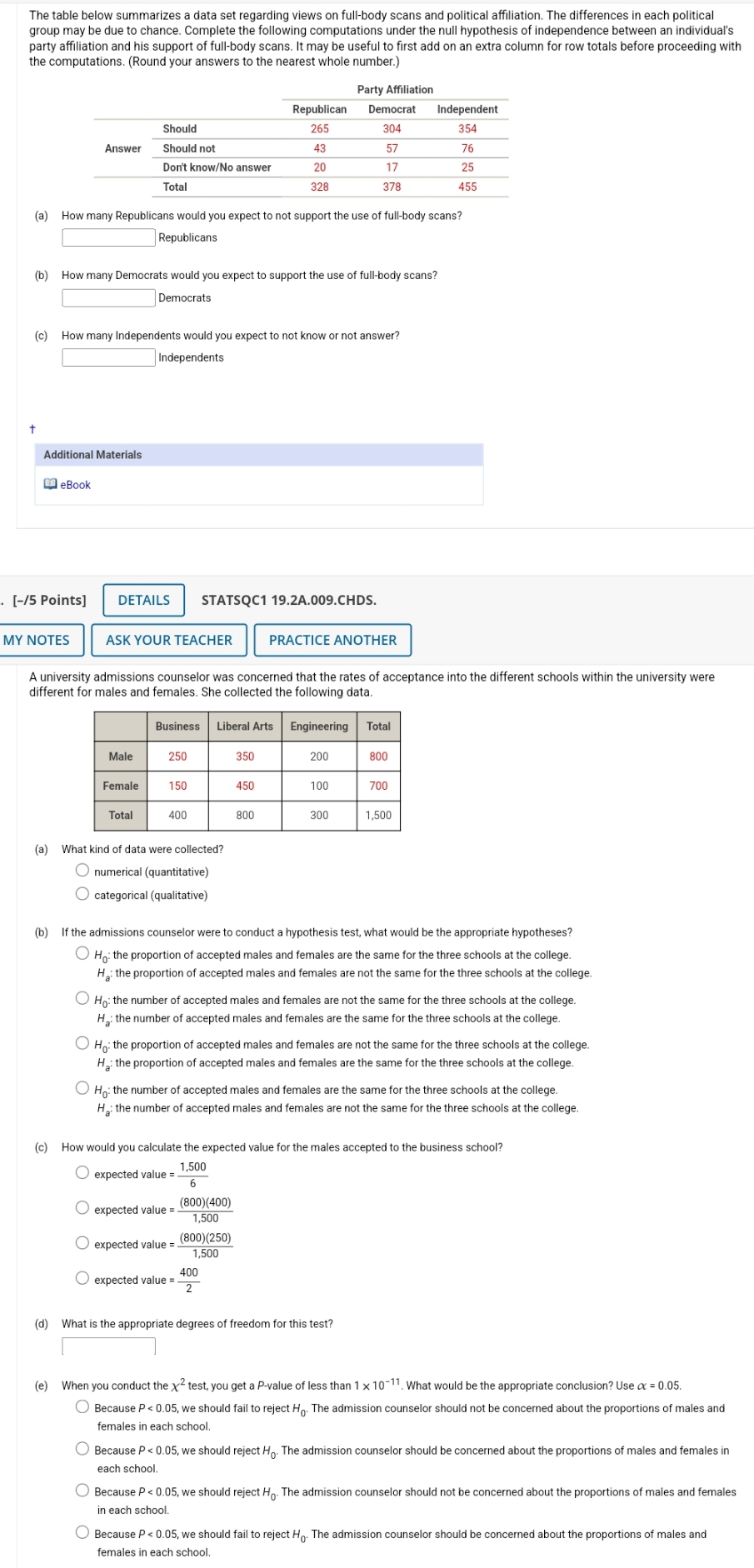
The table below summarizes a data set regarding views on full-body scans and political affiliation. The differences in each political group may be due to chance. Complete the following computations under the null hypothesis of independence between an individual's party affiliation and his support of full-body scans. It may be useful to first add on an extra column for row totals before proceeding with the computations. (Round your answers to the nearest whole number.) Party Affiliation Republican Democrat Independent Should 265 304 354 Answer Should not 43 57 76 Don't know/No answer 20 17 25 Total 328 378 455 (a) How many Republicans would you expect to not support the use of full-body scans? Republicans (b) How many Democrats would you expect to support the use of full-body scans? Democrats (c) How many Independents would you expect to not know or not answer? Independents Additional Materials eBook [-/5 Points] DETAILS STATSQC1 19.2A.009.CHDS. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER A university admissions counselor was concerned that the rates of acceptance into the different schools within the university were different for males and females. She collected the following data. Business Liberal Arts Engineering Total Male 250 350 200 800 Female 150 450 100 700 Total 400 800 300 1,500 (a) What kind of data were collected? numerical (quantitative) O categorical (qualitative) (b) If the admissions counselor were to conduct a hypothesis test, what would be the appropriate hypotheses? O Ho: the proportion of accepted males and females are the same for the three schools at the college. Ha: the proportion of accepted males and females are not the same for the three schools at the college. O Ho: the number of accepted males and females are not the same for the three schools at the college. Ha: the number of accepted males and females are the same for the three schools at the college. O Ho: the proportion of accepted males and females are not the same for the three schools at the college. Ha: the proportion of accepted males and females are the same for the three schools at the college. O Ho: the number of accepted males and females are the same for the three schools at the college. Ha: the number of accepted males and females are not the same for the three schools at the college. (c) How would you calculate the expected value for the males accepted to the business school? O expected value =_ - 1,500 6 expected value = (800)(400) 1,500 expected value = (800)(250) 1,500 expected value = _ 400 (d) What is the appropriate degrees of freedom for this test? (e) When you conduct the x2 test, you get a P-value of less than 1 x 10-11. What would be the appropriate conclusion? Use or = 0.05. O Because P