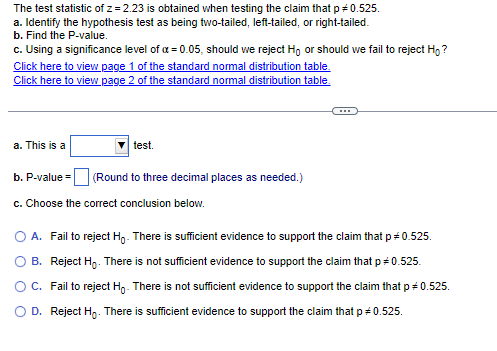
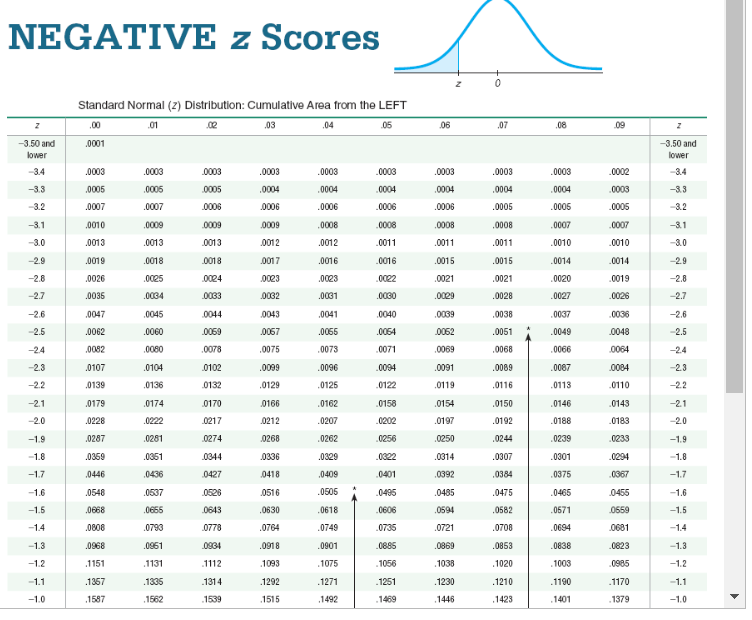
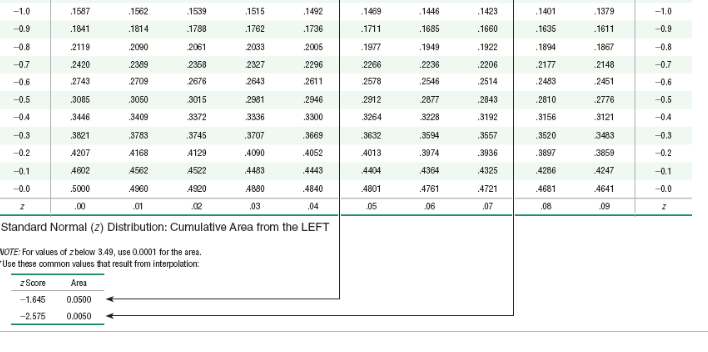
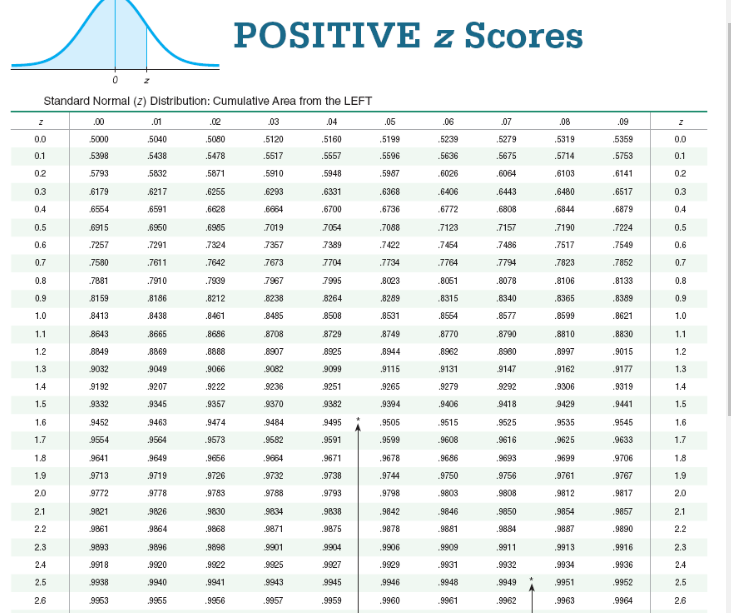
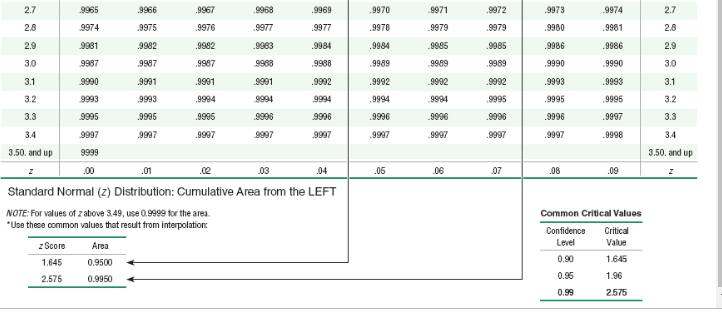
The test statistic of z = 2.23 is obtained when testing the claim that p = 0.525. a. Identify the hypothesis test as being two-tailed, left-tailed, or right-tailed. b. Find the P-value. c. Using a significance level of o = 0.05, should we reject Ho or should we fail to reject Ho? Click here to view page 1 of the standard normal distribution table. Click here to view page 2 of the standard normal distribution table. a. This is a test. b. P-value = (Round to three decimal places as needed.) c. Choose the correct conclusion below. O A. Fail to reject Ho. There is sufficient evidence to support the claim that p =0.525 O B. Reject Ho. There is not sufficient evidence to support the claim that p # 0.525. O C. Fail to reject Ho. There is not sufficient evidence to support the claim that p # 0.525. O D. Reject Ho. There is sufficient evidence to support the claim that p = 0.525.NEGATIVE z Scores 0 Standard Normal (Z) Distribution: Cumulative Area from the LEFT 09 ,00 102 03 .04 05 .06 .07 .08 -3.50 and -3.50 and .0001 lower lower 0002 3.4 3.4 0003 0003 0003 .0003 0003 10 03 0003 .0003 0003 0006 1005 004 0004 1004 0004 0004 0004 0003 -3.3 -3.3 0005 -3.2 .0007 .0007 0006 0006 0006 0006 .0006 0005 0005 0005 3.2 -3.1 .0010 .0009 0009 .0009 1008 10 08 .O008 0008 .0007 0007 -3.1 -3.0 0013 0013 0013 00 2 0012 0011 001 1 .0011 0010 0010 3.0 .0018 001 8 .0017 .0016 0016 .0015 1015 0014 0014 -2.9 -2.9 .0019 -2.8 .0020 0025 0024 0023 .0023 0022 0021 0021 0020 0019 -2.8 2.7 .0035 .0034 0033 10032 .0031 .0030 .0029 0028 .0027 .0026 -2.7 -2.6 0047 0045 0044 0043 .0041 0040 .0039 0038 0037 0036 -2.6 1060 0059 0057 .0055 0064 0062 .0051 .0049 0048 2.5 -2.5 .0062 0082 1080 0078 0075 0073 0071 0069 .0068 0066 0064 -24 -24 .0104 0102 .0099 0096 0094 .0091 0089 0087 0084 -2.3 -2.3 .0107 .0113 0110 -2.2 -2.2 .0139 .0136 0132 .0129 0126 0122 .0119 0116 0179 .0174 0170 0166 0162 0158 0154 0150 0146 0143 -2.1 -2.1 -2.0 .0228 .0222 0217 0212 0207 0202 0197 .0192 0188 0183 -20 .0287 .0251 1274 0268 0262 .0256 .0250 .0244 .0239 0233 -1.9 -1.9 -1.8 .0359 .0351 0344 .0336 0329 0322 .0314 0307 .0301 0294 1.8 0436 0427 0418 .0409 0401 0392 ,0384 0375 0367 -1.7 -1.7 0446 -1.6 .0540 .0537 0526 .0516 .0505 .0495 0485 .0475 0465 0455 -1.6 .0668 .0665 0643 .0630 .0618 0606 .0594 0582 .0571 0659 -1.5 -1.6 -1.4 -1.4 .0808 .0790 0778 0764 0749 0735 0721 0708 0694 0681 -1.3 .0968 0961 0934 0918 0901 0885 0869 0853 0838 0823 -1.3 -1112 1093 1075 1056 1038 1020 1003 0985 -1.2 -1.2 .1151 .1131 -1.1 -1.1 .1357 . 1335 .1314 1292 .1271 1251 1230 .1210 .1190 .1170 1379 -1.0 -10 .1587 .1562 1539 .1515 .1492 1459 .1446 1423 .1401-1.0 .1597 ,1562 1539 1515 .1492 .1459 1446 .1423 .1401 .1379 -1.0 -0.9 .1841 .1814 1788 .1762 .1736 .1711 .1685 .1660 .1635 1611 0.9 -0.8 .2119 .2080 2061 2033 2005 1977 . 1949 .1922 .1894 -1867 -0.8 -0.7 .2420 2389 2350 2327 .2296 2266 2236 2206 .2177 2148 0.7 0.6 .2743 2709 2676 2643 2611 2578 2546 2514 2493 2451 -0.6 -0.5 .3085 .3050 3015 2981 .2940 2912 2877 .2843 2810 2776 -0.5 -04 .3446 .3409 3372 3336 .3300 3264 3228 .3192 .3156 .3121 -04 -0.3 3821 3783 3745 3707 3669 36:32 3594 .3557 .3520 3483 -0.3 -0.2 .4207 4168 4129 .4090 .4052 4013 .3074 .3936 .3897 3859 0.2 -0.1 4602 4562 4522 .4483 4443 4404 4364 4325 .4286 4247 -0.1 0.0 .5000 4960 4920 4890 .4840 4801 .4761 .4721 4681 4641 0.0 ,00 .01 02 .03 .04 05 06 .07 08 09 Standard Normal (2) Distribution: Cumulative Area from the LEFT VOTE: For values of zbelow 3.49, use 0.0001 for the area. Use these common values that result from interpolation. z Score Area -1.645 0.0500 -2.576 0,0050POSITIVE z Scores Standard Normal (z) Distribution: Cumulative Area from the LEFT .De 102 03 .04 .05 06 107 0.0 0.0 5000 .5040 5080 ,6120 5160 5199 5239 .6279 5319 5369 5753 0.1 0.1 5308 .5438 .5478 .6517 5557 5596 5636 .5675 5714 6064 6103 6141 0.2 0.2 5793 5832 5871 5910 5948 5987 8026 6179 6217 6255 6293 .6331 6368 .6406 .6443 .6480 6517 0.3 0.3 6591 6628 6864 6700 6736 6772 .6808 . 6844 6879 0.4 0.4 6564 6895 7019 7054 .7080 .7123 7157 7190 7224 0.5 0.5 8915 6950 .7291 .7324 7357 7389 .7422 -7454 .7486 .7517 .7549 0.6 0.6 .7257 0.7 0.7 7580 ,7611 7642 7673 7704 7734 7764 7794 7823 7852 0.8 .7881 .7910 .7939 7967 7905 .8023 .8061 .8078 .8106 8133 0.8 8238 8264 8289 8315 ,8340 ,8365 83.89 0.9 0.9 8159 8186 8212 .8461 848 8508 .8531 .8554 8577 .8599 8621 1.0 1.0 8413 .8438 1.1 3643 1665 8696 8708 8728 8749 8770 8790 8810 8830 1.1 8997 9015 1.2 1.2 0849 .0869 0808 8907 8925 8944 1962 8900 .9162 9177 1.3 1.3 9032 .9049 9066 9099 9115 9131 9147 9292 .9306 9319 14 1.4 9192 .9207 9222 .9236 9251 9265 9279 1.5 9332 1345 9357 8370 9382 9394 9406 9418 9429 9441 1.6 1.6 9452 9463 1474 9484 9495 9505 9515 9525 9535 9545 1.6 .9625 9633 1.7 1.7 9554 .9564 9573 .9582 9591 9509 1608 .9616 1.8 9641 .9649 .9656 9664 .9671 9678 96-86 .9693 .9699 9706 1.8 .9732 9730 9744 9750 9756 9761 9767 1.9 1.9 9713 .9719 9726 9772 778 9783 978 9793 9798 9803 1808 9812 9817 2.0 2.0 1821 1826 9830 9834 9838 9842 9846 .9850 9854 9857 2.1 2.1 2.2 9861 .9864 9868 9871 .9875 9878 9281 .8384 .9887 9890 2.2 9893 9896 9896 9901 9904 .9906 9909 9911 .9913 9916 2.3 2.3 9825 9927 9529 9931 8932 9934 .9936 2.4 2.4 991 8 .9920 9922 2.5 9938 9940 9841 9943 9945 9946 1948 9949 9951 9962 2.5 .9962 9963 9964 2.6 2.6 1953 1955 9950 .9957 995 9960 99612.7 9865 .9866 .9967 8968 .9969 .9970 9971 .8972 .9973 .9974 2.7 2.8 9974 .9975 9976 .9977 9977 9970 9979 9979 9980 9981 2.6 2.9 9881 .9982 .9982 .9083 .9084 .9984 .9985 9085 .9086 .9986 2.9 3.0 9987 .9957 9957 9988 .9988 .9989 9989 .9489 .9990 .9990 3.0 3.1 9990 .9991 9991 9991 .9992 9992 9992 .9993 9993 3.1 3.2 9993 .9993 .9984 0904 9994 .9894 .9984 9995 .9995 .9996 3.2 3.3 9995 .9995 .9995 9996 9996 .9996 .9946 .9096 .9996 .9997 3.3 3.4 9897 .9997 .9987 8997 9897 .9997 .9987 8997 .9997 . 9998 3.4 3.50. and up 9999 3.50, and up .00 .01 02 03 .04 05 06 07 .08 .09 Standard Normal (z) Distribution: Cumulative Area from the LEFT NOTE: For values of z above 3.49, use 0.9899 for the area. *Use these common values that result from interpolations Common Critical Values Confidence Critical z Score Area Level Value 1.645 0.9500 0.90 1.645 2.575 0.9950 0.95 1.96 0.99 2 575