Answered step by step
Verified Expert Solution
Question
1 Approved Answer
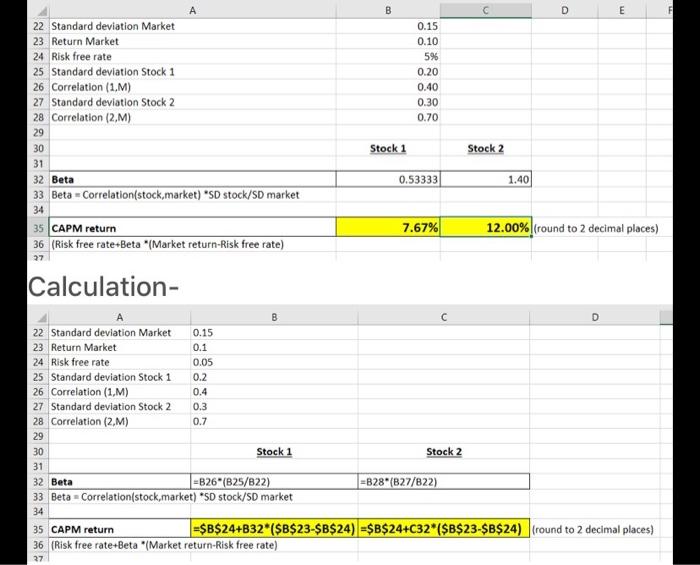
the third and fourth pictures are more information thats needed for the question on picture 3. Consider the following properties of the return of stock
the third and fourth pictures are more information thats needed for the question on picture 3. 



Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


