The time series plot in the following graph shows Discount Soda's (Egdworth) for the recorded monthly Cola sales for the three years 2003 to
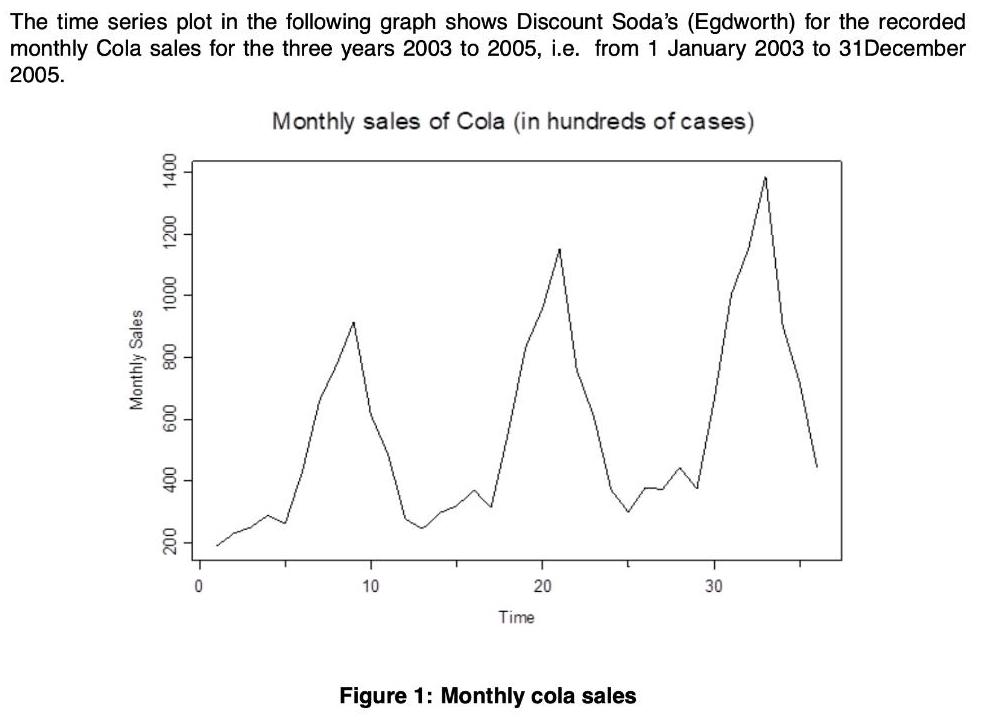



The time series plot in the following graph shows Discount Soda's (Egdworth) for the recorded monthly Cola sales for the three years 2003 to 2005, i.e. from 1 January 2003 to 31December 2005. Monthly sales of Cola (in hundreds of cases) 10 20 30 Time Figure 1: Monthly cola sales 000 0001 008 009 007 Monthly Sales (a) Which of the two models, Y; = TN; x CL; SN; x IR; and Y; = TN; + CL; + SN; + IN, %3D where TN, CL, SN, IR, are trend, cyclical, seasonal and irregular components respec- tively, would you suggest adequately fits the untransformed and log transformed series data? Give a reason(s) for your answer. (3) (b) Which operator(s) of transformation would you apply to this series to make it stationary? (2) (c) A log transformation of the Cola sales data suggests that the seasonality is constant. Hence, the seasonal model using trigonometric functions, Z; = Bo + Bit +B2 sin (@t) + B3 cos (@t) + E1, %3D 2n t is the time index, L is the seasonality period and L where Z, log (Y;), w = Et ~ N (0, o?), can be used. The multiple regression equation in vector-matrix is Z = XB + e. Write down the design matrix X for the above model. (3) (d) Table 6.1 gives the R-output for the model in (c) fitted for the series. Table 6.1: Estimation of deterministic linear trend and seasonality via sinusoidal functions fit It) < 2e-16 *** 1.71e-06 * ** 3.20e-15 *** 1.34e-05 *** (Intercept) 5.885193 0.059846 98.339 0.016622 0.002844 5.844 0 sin ot -0.584950 0.041690 -14.031 cos ot -0.207521 0.040416 -5.135 --- Signif. codes: 0 ***' 0.001 ***' 0.01 0.05 .'0.1 '1 Residual standard error: 0.171 on 32 degrees of freedom Multiple R-Squared: 0.9075, F-statistic: 104.7 on 3 and 32 DF, p-value: < 2.2e-16 Adjusted R-squared: 0.8989 (i) Give the value of the angular frequency o which accounts for the seasonality exhibited. (2) (ii) Write down the estimated model in Table 6.1. (3) (iii) Taking into account both the seasonality and trend components find the transformed forecasts for both January and February of 2006, i.e. ; (37) and 2; (38) and their re- spective prediction limits. (Hint: z373 [1 37 sin(37) cos(37)]). (4) (iv) Taking into account both the seasonality and trend components, find the minimum mean square error forecast in the original series forecasts for both January and February of 2006, i.e. , (37) and , (38) and their respective prediction limits. (6) (Hint: The minimum mean square error forecast is given by exp {2, (1) +Var[e,1)]}, where Var[e,(1)1 = 62 = 0.1712), %3D The time series plot in the following graph shows Discount Soda's (Egdworth) for the recorded monthly Cola sales for the three years 2003 to 2005, i.e. from 1 January 2003 to 31December 2005. Monthly sales of Cola (in hundreds of cases) 10 20 30 Time Figure 1: Monthly cola sales 000 0001 008 009 007 Monthly Sales (a) Which of the two models, Y; = TN; x CL; SN; x IR; and Y; = TN; + CL; + SN; + IN, %3D where TN, CL, SN, IR, are trend, cyclical, seasonal and irregular components respec- tively, would you suggest adequately fits the untransformed and log transformed series data? Give a reason(s) for your answer. (3) (b) Which operator(s) of transformation would you apply to this series to make it stationary? (2) (c) A log transformation of the Cola sales data suggests that the seasonality is constant. Hence, the seasonal model using trigonometric functions, Z; = Bo + Bit +B2 sin (@t) + B3 cos (@t) + E1, %3D 2n t is the time index, L is the seasonality period and L where Z, log (Y;), w = Et ~ N (0, o?), can be used. The multiple regression equation in vector-matrix is Z = XB + e. Write down the design matrix X for the above model. (3) (d) Table 6.1 gives the R-output for the model in (c) fitted for the series. Table 6.1: Estimation of deterministic linear trend and seasonality via sinusoidal functions fit It) < 2e-16 *** 1.71e-06 * ** 3.20e-15 *** 1.34e-05 *** (Intercept) 5.885193 0.059846 98.339 0.016622 0.002844 5.844 0 sin ot -0.584950 0.041690 -14.031 cos ot -0.207521 0.040416 -5.135 --- Signif. codes: 0 ***' 0.001 ***' 0.01 0.05 .'0.1 '1 Residual standard error: 0.171 on 32 degrees of freedom Multiple R-Squared: 0.9075, F-statistic: 104.7 on 3 and 32 DF, p-value: < 2.2e-16 Adjusted R-squared: 0.8989 (i) Give the value of the angular frequency o which accounts for the seasonality exhibited. (2) (ii) Write down the estimated model in Table 6.1. (3) (iii) Taking into account both the seasonality and trend components find the transformed forecasts for both January and February of 2006, i.e. ; (37) and 2; (38) and their re- spective prediction limits. (Hint: z373 [1 37 sin(37) cos(37)]). (4) (iv) Taking into account both the seasonality and trend components, find the minimum mean square error forecast in the original series forecasts for both January and February of 2006, i.e. , (37) and , (38) and their respective prediction limits. (6) (Hint: The minimum mean square error forecast is given by exp {2, (1) +Var[e,1)]}, where Var[e,(1)1 = 62 = 0.1712), %3D The time series plot in the following graph shows Discount Soda's (Egdworth) for the recorded monthly Cola sales for the three years 2003 to 2005, i.e. from 1 January 2003 to 31December 2005. Monthly sales of Cola (in hundreds of cases) 10 20 30 Time Figure 1: Monthly cola sales 000 0001 008 009 007 Monthly Sales (a) Which of the two models, Y; = TN; x CL; SN; x IR; and Y; = TN; + CL; + SN; + IN, %3D where TN, CL, SN, IR, are trend, cyclical, seasonal and irregular components respec- tively, would you suggest adequately fits the untransformed and log transformed series data? Give a reason(s) for your answer. (3) (b) Which operator(s) of transformation would you apply to this series to make it stationary? (2) (c) A log transformation of the Cola sales data suggests that the seasonality is constant. Hence, the seasonal model using trigonometric functions, Z; = Bo + Bit +B2 sin (@t) + B3 cos (@t) + E1, %3D 2n t is the time index, L is the seasonality period and L where Z, log (Y;), w = Et ~ N (0, o?), can be used. The multiple regression equation in vector-matrix is Z = XB + e. Write down the design matrix X for the above model. (3) (d) Table 6.1 gives the R-output for the model in (c) fitted for the series. Table 6.1: Estimation of deterministic linear trend and seasonality via sinusoidal functions fit It) < 2e-16 *** 1.71e-06 * ** 3.20e-15 *** 1.34e-05 *** (Intercept) 5.885193 0.059846 98.339 0.016622 0.002844 5.844 0 sin ot -0.584950 0.041690 -14.031 cos ot -0.207521 0.040416 -5.135 --- Signif. codes: 0 ***' 0.001 ***' 0.01 0.05 .'0.1 '1 Residual standard error: 0.171 on 32 degrees of freedom Multiple R-Squared: 0.9075, F-statistic: 104.7 on 3 and 32 DF, p-value: < 2.2e-16 Adjusted R-squared: 0.8989 (i) Give the value of the angular frequency o which accounts for the seasonality exhibited. (2) (ii) Write down the estimated model in Table 6.1. (3) (iii) Taking into account both the seasonality and trend components find the transformed forecasts for both January and February of 2006, i.e. ; (37) and 2; (38) and their re- spective prediction limits. (Hint: z373 [1 37 sin(37) cos(37)]). (4) (iv) Taking into account both the seasonality and trend components, find the minimum mean square error forecast in the original series forecasts for both January and February of 2006, i.e. , (37) and , (38) and their respective prediction limits. (6) (Hint: The minimum mean square error forecast is given by exp {2, (1) +Var[e,1)]}, where Var[e,(1)1 = 62 = 0.1712), %3D The time series plot in the following graph shows Discount Soda's (Egdworth) for the recorded monthly Cola sales for the three years 2003 to 2005, i.e. from 1 January 2003 to 31December 2005. Monthly sales of Cola (in hundreds of cases) 10 20 30 Time Figure 1: Monthly cola sales 000 0001 008 009 007 Monthly Sales (a) Which of the two models, Y; = TN; x CL; SN; x IR; and Y; = TN; + CL; + SN; + IN, %3D where TN, CL, SN, IR, are trend, cyclical, seasonal and irregular components respec- tively, would you suggest adequately fits the untransformed and log transformed series data? Give a reason(s) for your answer. (3) (b) Which operator(s) of transformation would you apply to this series to make it stationary? (2) (c) A log transformation of the Cola sales data suggests that the seasonality is constant. Hence, the seasonal model using trigonometric functions, Z; = Bo + Bit +B2 sin (@t) + B3 cos (@t) + E1, %3D 2n t is the time index, L is the seasonality period and L where Z, log (Y;), w = Et ~ N (0, o?), can be used. The multiple regression equation in vector-matrix is Z = XB + e. Write down the design matrix X for the above model. (3) (d) Table 6.1 gives the R-output for the model in (c) fitted for the series. Table 6.1: Estimation of deterministic linear trend and seasonality via sinusoidal functions fit It) < 2e-16 *** 1.71e-06 * ** 3.20e-15 *** 1.34e-05 *** (Intercept) 5.885193 0.059846 98.339 0.016622 0.002844 5.844 0 sin ot -0.584950 0.041690 -14.031 cos ot -0.207521 0.040416 -5.135 --- Signif. codes: 0 ***' 0.001 ***' 0.01 0.05 .'0.1 '1 Residual standard error: 0.171 on 32 degrees of freedom Multiple R-Squared: 0.9075, F-statistic: 104.7 on 3 and 32 DF, p-value: < 2.2e-16 Adjusted R-squared: 0.8989 (i) Give the value of the angular frequency o which accounts for the seasonality exhibited. (2) (ii) Write down the estimated model in Table 6.1. (3) (iii) Taking into account both the seasonality and trend components find the transformed forecasts for both January and February of 2006, i.e. ; (37) and 2; (38) and their re- spective prediction limits. (Hint: z373 [1 37 sin(37) cos(37)]). (4) (iv) Taking into account both the seasonality and trend components, find the minimum mean square error forecast in the original series forecasts for both January and February of 2006, i.e. , (37) and , (38) and their respective prediction limits. (6) (Hint: The minimum mean square error forecast is given by exp {2, (1) +Var[e,1)]}, where Var[e,(1)1 = 62 = 0.1712), %3D
Step by Step Solution
3.45 Rating (164 Votes )
There are 3 Steps involved in it
Step: 1
Generally two types of models are used in time series forecasting 1 Additive model such as ...
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


