The total world population is forecast to be P(t) = 0.00069t - 0.0699t2 + 0.8t + 6.04 (0

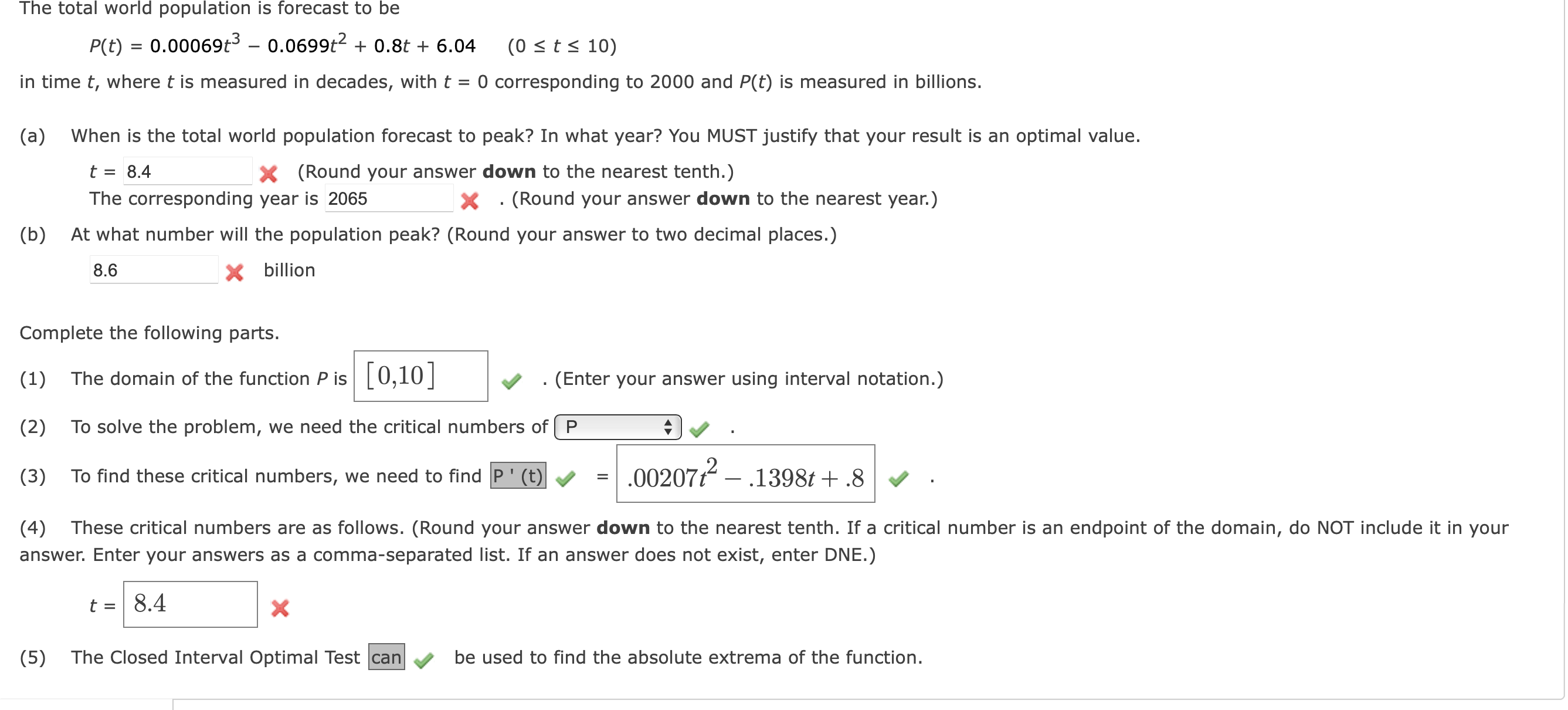
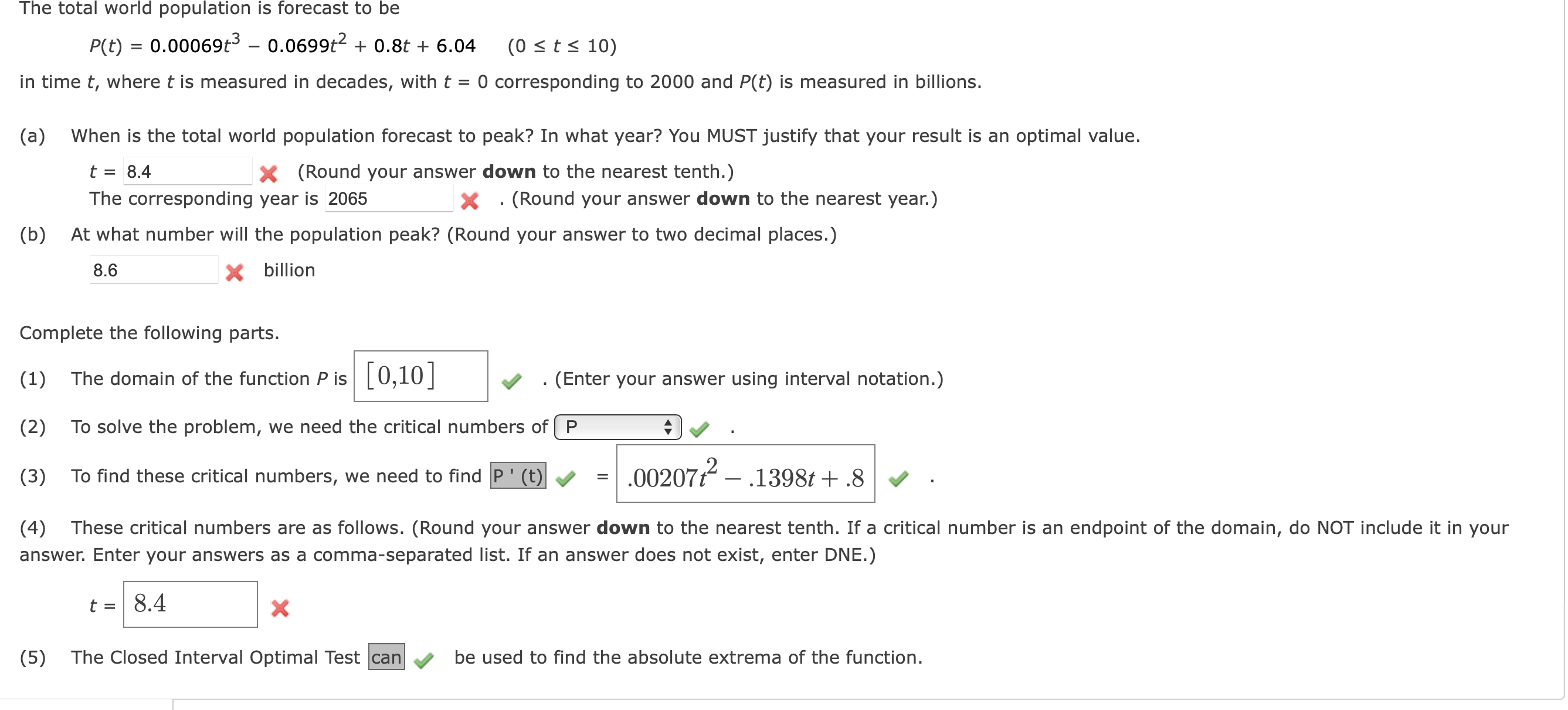
The total world population is forecast to be P(t) = 0.00069t3 - 0.06998 + 0.8t + 6.04 (0 10) in time t, where t is measured in decades, with t = O corresponding to 2000 and P(t) is measured in billions. (a) (b) When is the total world population forecast to peak? In what year? You MUST justify that your result is an optimal value. t = 8.4 (Round your answer down to the nearest tenth.) x The corresponding year is 2065 . (Round your answer down to the nearest year.) x At what number will the population peak? (Round your answer to two decimal places.) 8.6 X billion Complete the following parts. (1) The domain of the function P is [O, 10] (Enter your answer using interval notation.) (2) To solve the problem, we need the critical numbers Of (3) To find these critical numbers, we need to find 2 .00207t -.1398t+ .8 (4) These critical numbers are as follows. (Round your answer down to the nearest tenth. If a critical number is an endpoint of the domain, do NOT include it in your answer. Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.) (5) The Closed Interval Optimal Test can be used to find the absolute extrema of the function.