The use of three estimates (defined here as H=high, L=low, and M=most likely) for random variables is a practical technique for modeling uncertainty in some engineering economy studies. Assume that the mean and variance of the random variable, Xk, in this situation can be estimated by E(Xk) =(1/6)(H+4M+L) and V(Xk) =[(HL)/6]2. The random variables,Xk , are assumed to be statistically independent, and the applicable MARR=15% per year.

What are the mean and variance of the PW?

E(PW)=$ (Round to the nearest dollar.)

V(PW)=enter your response here ($)^2 million (Round to three decimal places.)

Part 3

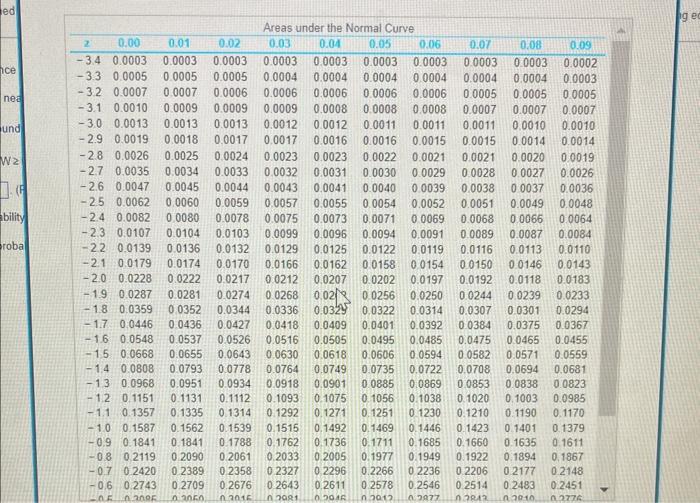
b. What is the probability that PW0? Assume that the PW of the net cash flow is a normally distributed random variable with =E(PW) and 2=V(PW).

The probability that PW0 is (enter your response here.) (Round to four decimal places.)

Part 4

c. Is this the same as the probability that the IRR is acceptable?.

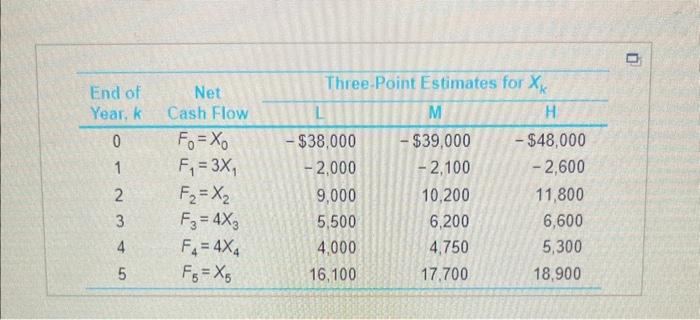
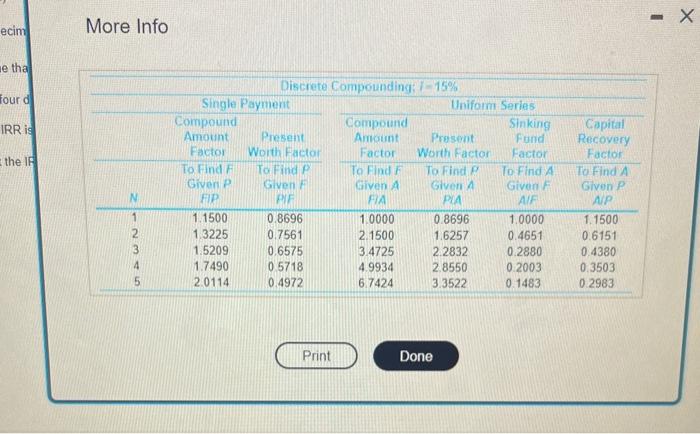
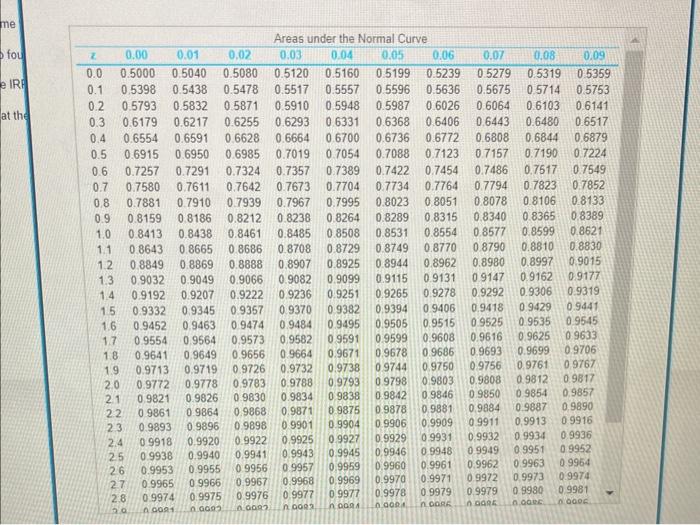
2. What aee Be san and wa ance ot the PW? The fratativy the \begin{tabular}{ccrrr} End of & Net & \multicolumn{3}{c}{ Three-Point Estimates for Xk} \\ Year, k & Cash Flow & \multicolumn{1}{c}{L} & M \\ \hline 0 & F0=X0 & $38,000 & $39,000 & $48,000 \\ 1 & F1=3X1 & 2,000 & 2,100 & 2,600 \\ 2 & F2=X2 & 9,000 & 10,200 & 11,800 \\ 3 & F3=4X3 & 5,500 & 6,200 & 6,600 \\ 4 & F4=4X4 & 4,000 & 4,750 & 5,300 \\ 5 & F5=X5 & 16,100 & 17,700 & 18,900 \\ \hline & & & & \end{tabular} More Info \begin{tabular}{ccccccccccccc} \hline \multicolumn{10}{|c|c}{ Areas under the Normal Curve } \\ \hline z. & 0.00 & 0.01 & 0.02 & 0.03 & 0.04 & 0.05 & 0.06 & 0.07 & 0.08 & 0.09 \\ \hline 0.0 & 0.5000 & 0.5040 & 0.5080 & 0.5120 & 0.5160 & 0.5199 & 0.5239 & 0.5279 & 0.5319 & 0.5359 \\ 0.1 & 0.5398 & 0.5438 & 0.5478 & 0.5517 & 0.5557 & 0.5596 & 0.5636 & 0.5675 & 0.5714 & 0.5753 \\ 0.2 & 0.5793 & 0.5832 & 0.5871 & 0.5910 & 0.5948 & 0.5987 & 0.6026 & 0.6064 & 0.6103 & 0.6141 \\ 0.3 & 0.6179 & 0.6217 & 0.6255 & 0.6293 & 0.6331 & 0.6368 & 0.6406 & 0.6443 & 0.6480 & 0.6517 \\ 0.4 & 0.6554 & 0.6591 & 0.6628 & 0.6664 & 0.6700 & 0.6736 & 0.6772 & 0.6808 & 0.6844 & 0.6879 \\ 0.5 & 0.6915 & 0.6950 & 0.6985 & 0.7019 & 0.7054 & 0.7088 & 0.7123 & 0.7157 & 0.7190 & 0.7224 \\ 0.6 & 0.7257 & 0.7291 & 0.7324 & 0.7357 & 0.7389 & 0.7422 & 0.7454 & 0.7486 & 0.7517 & 0.7549 \\ 0.7 & 0.7580 & 0.7611 & 0.7642 & 0.7673 & 0.7704 & 0.7734 & 0.7764 & 0.7794 & 0.7823 & 0.7852 \\ 0.8 & 0.7881 & 0.7910 & 0.7939 & 0.7967 & 0.7995 & 0.8023 & 0.8051 & 0.8078 & 0.8106 & 0.8133 \\ 0.9 & 0.8159 & 0.8186 & 0.8212 & 0.8238 & 0.8264 & 0.8289 & 0.8315 & 0.8340 & 0.8365 & 0.8389 \\ 1.0 & 0.8413 & 0.8438 & 0.8461 & 0.8485 & 0.8508 & 0.8531 & 0.8554 & 0.8577 & 0.8599 & 0.8621 \\ 1.1 & 0.8643 & 0.8665 & 0.8686 & 0.8708 & 0.8729 & 0.8749 & 0.8770 & 0.8790 & 0.8810 & 0.8830 \\ 1.2 & 0.8849 & 0.8869 & 0.8888 & 0.8907 & 0.8925 & 0.8944 & 0.8962 & 0.8980 & 0.8997 & 0.9015 \\ 1.3 & 0.9032 & 0.9049 & 0.9066 & 0.9082 & 0.9099 & 0.9115 & 0.9131 & 0.9147 & 0.9162 & 0.9177 \\ 1.4 & 0.9192 & 0.9207 & 0.9222 & 0.9236 & 0.9251 & 0.9265 & 0.9278 & 0.9292 & 0.9306 & 0.9319 \\ 1.5 & 0.9332 & 0.9345 & 0.9357 & 0.9370 & 0.9382 & 0.9394 & 0.9406 & 0.9418 & 0.9429 & 0.9441 \\ 1.6 & 0.9452 & 0.9463 & 0.9474 & 0.9484 & 0.9495 & 0.9505 & 0.9515 & 0.9525 & 0.9535 & 0.9545 \\ 1.7 & 0.9554 & 0.9564 & 0.9573 & 0.9582 & 0.9591 & 0.9599 & 0.9608 & 0.9616 & 0.9625 & 09633 \\ 1.8 & 0.9641 & 0.9649 & \end{tabular}