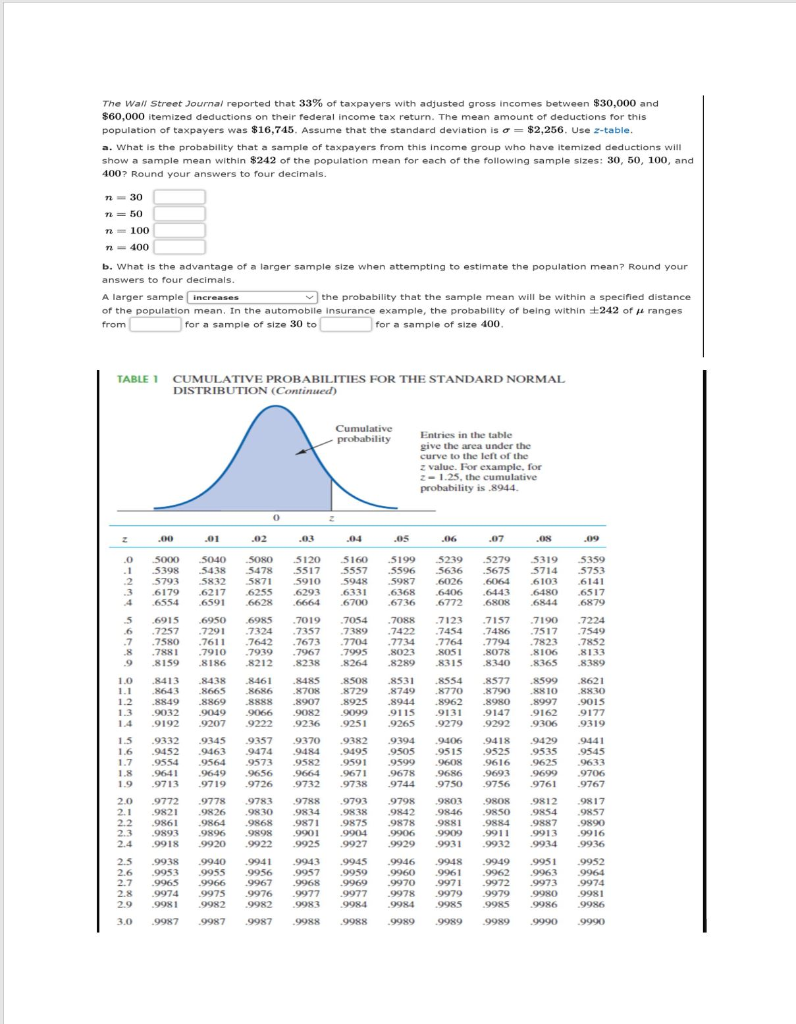
The Wall Street Journal reported that 33% of taxpayers with adjusted gross incomes between $30,000 and $60,000 itemized deductions on their federal income tax return. The mean amount of deductions for this population of taxpayers was $16,745. Assume that the standard deviation is o = $2,256. Use 2-table. a. What is the probability that a sample of taxpayers from this income group who have itemized deductions will show a sample mean within $242 of the population mean for each of the following sample sizes: 30, 50, 100, and 400? Round your answers to four decimals. n30 n =50 n 100 n = 400 b. What is the advantage of a larger sample size when attempting to estimate the population mean? Round your answers to four decimals. A larger sample increases the probability that the sample mean will be within a specified distance of the population mean. In the automobile insurance example, the probability of being within +242 of He ranges from for a sample of size 30 to for a sample of size 400. TABLE 1 CUMULATIVE PROBABILITIES FOR THE STANDARD NORMAL DISTRIBUTION (Continued) Cumulative probability Entries in the table give the area under the curve to the left of the z value. For example, for 2-1.25, the cumulative probability is .8944 0 .00 .01 .02 .04 05 .07 .08 .09 .0 .1 .2 5279 .5675 SONO 5478 5871 .6255 .6628 5199 .5596 .5987 .6368 .6736 5319 5714 .6103 .6480 5359 .5753 .6141 .6517 .6879 4 680R 5000 5398 5793 .6179 .6554 .6915 .7257 .7580 .7881 .8159 5040 .5438 .5832 .6217 .6591 .6950 7291 .7611 .7910 .8186 5120 5517 .5910 .6293 .6664 .7019 .7357 .7673 .7967 .8238 5160 5557 59:48 .6331 .6700 .7054 .7389 .7704 .7995 8264 5 6 .7 .6985 .7324 .7642 .7939 .8212 .7157 7486 .7794 .8078 .8340 .7190 .7517 .7823 .8106 .8365 .7224 .7549 .7852 .8133 8389 9 1.0 1.1 1.2 1.3 .8413 .8643 8849 9032 .9192 .8438 8665 .8869 9049 .9207 .8461 8686 .8888 9066 9222 .8485 .8708 .8907 9082 .9236 .7088 .7422 .7734 .8023 .8289 .8531 8749 .8944 9115 .9265 .9394 .9505 .9599 5239 5636 .6026 .6406 .6772 .7123 .7454 .7764 8051 .8315 .8554 .8770 8962 9131 .9279 9406 .9515 9608 .9686 9750 .9803 9846 9881 .9909 9931 .8577 .8790 .8980 .9147 9292 .8599 .8810 .8997 9162 9305 8621 8810 9015 9177 .9319 1.5 1.6 1.7 1.8 1.9 .9332 9452 .9554 .9641 9713 .9345 9463 9564 8508 8729 .8925 9099 9251 9382 9495 9591 .9671 .9738 .9793 9838 9875 .9904 .9927 9357 .9474 .9573 .9656 9726 9418 9525 9616 .9693 .9756 9441 9545 .9633 9706 9767 .9649 .9678 9719 2.0 2.1 2.2 2.3 2.4 .9772 .9821 .9861 .9893 .9918 9783 .9830 .9868 9898 .9922 9370 9484 9582 .9664 9732 9788 9834 .9871 .9201 9925 .9943 9957 .9968 9977 9983 9744 .9798 .9842 .9878 .9906 .9929 .9946 9960 .9970 9978 9984 .9778 9826 9864 9896 .9920 9940 9955 .9966 9975 9982 9987 .9808 .9850 .9884 9911 .9932 9949 9962 29972 9979 9429 .9535 .9625 9699 .9761 .9812 .9854 .9887 9913 .9934 .9951 9963 .9973 9980 9986 .9990 9817 9857 9890 .9916 9936 9952 9964 .9974 9981 9986 2.5 2.6 2.7 2.8 2.9 .9938 9953 9965 .9974 .9981 9987 .9941 9956 9967 9976 9982 .9987 9945 .9959 .9969 9977 9984 .9988 9948 9961 9971 9979 9985 9985 3.0 9988 9989 9989 9989 9990 The Wall Street Journal reported that 33% of taxpayers with adjusted gross incomes between $30,000 and $60,000 itemized deductions on their federal income tax return. The mean amount of deductions for this population of taxpayers was $16,745. Assume that the standard deviation is o = $2,256. Use 2-table. a. What is the probability that a sample of taxpayers from this income group who have itemized deductions will show a sample mean within $242 of the population mean for each of the following sample sizes: 30, 50, 100, and 400? Round your answers to four decimals. n30 n =50 n 100 n = 400 b. What is the advantage of a larger sample size when attempting to estimate the population mean? Round your answers to four decimals. A larger sample increases the probability that the sample mean will be within a specified distance of the population mean. In the automobile insurance example, the probability of being within +242 of He ranges from for a sample of size 30 to for a sample of size 400. TABLE 1 CUMULATIVE PROBABILITIES FOR THE STANDARD NORMAL DISTRIBUTION (Continued) Cumulative probability Entries in the table give the area under the curve to the left of the z value. For example, for 2-1.25, the cumulative probability is .8944 0 .00 .01 .02 .04 05 .07 .08 .09 .0 .1 .2 5279 .5675 SONO 5478 5871 .6255 .6628 5199 .5596 .5987 .6368 .6736 5319 5714 .6103 .6480 5359 .5753 .6141 .6517 .6879 4 680R 5000 5398 5793 .6179 .6554 .6915 .7257 .7580 .7881 .8159 5040 .5438 .5832 .6217 .6591 .6950 7291 .7611 .7910 .8186 5120 5517 .5910 .6293 .6664 .7019 .7357 .7673 .7967 .8238 5160 5557 59:48 .6331 .6700 .7054 .7389 .7704 .7995 8264 5 6 .7 .6985 .7324 .7642 .7939 .8212 .7157 7486 .7794 .8078 .8340 .7190 .7517 .7823 .8106 .8365 .7224 .7549 .7852 .8133 8389 9 1.0 1.1 1.2 1.3 .8413 .8643 8849 9032 .9192 .8438 8665 .8869 9049 .9207 .8461 8686 .8888 9066 9222 .8485 .8708 .8907 9082 .9236 .7088 .7422 .7734 .8023 .8289 .8531 8749 .8944 9115 .9265 .9394 .9505 .9599 5239 5636 .6026 .6406 .6772 .7123 .7454 .7764 8051 .8315 .8554 .8770 8962 9131 .9279 9406 .9515 9608 .9686 9750 .9803 9846 9881 .9909 9931 .8577 .8790 .8980 .9147 9292 .8599 .8810 .8997 9162 9305 8621 8810 9015 9177 .9319 1.5 1.6 1.7 1.8 1.9 .9332 9452 .9554 .9641 9713 .9345 9463 9564 8508 8729 .8925 9099 9251 9382 9495 9591 .9671 .9738 .9793 9838 9875 .9904 .9927 9357 .9474 .9573 .9656 9726 9418 9525 9616 .9693 .9756 9441 9545 .9633 9706 9767 .9649 .9678 9719 2.0 2.1 2.2 2.3 2.4 .9772 .9821 .9861 .9893 .9918 9783 .9830 .9868 9898 .9922 9370 9484 9582 .9664 9732 9788 9834 .9871 .9201 9925 .9943 9957 .9968 9977 9983 9744 .9798 .9842 .9878 .9906 .9929 .9946 9960 .9970 9978 9984 .9778 9826 9864 9896 .9920 9940 9955 .9966 9975 9982 9987 .9808 .9850 .9884 9911 .9932 9949 9962 29972 9979 9429 .9535 .9625 9699 .9761 .9812 .9854 .9887 9913 .9934 .9951 9963 .9973 9980 9986 .9990 9817 9857 9890 .9916 9936 9952 9964 .9974 9981 9986 2.5 2.6 2.7 2.8 2.9 .9938 9953 9965 .9974 .9981 9987 .9941 9956 9967 9976 9982 .9987 9945 .9959 .9969 9977 9984 .9988 9948 9961 9971 9979 9985 9985 3.0 9988 9989 9989 9989 9990







