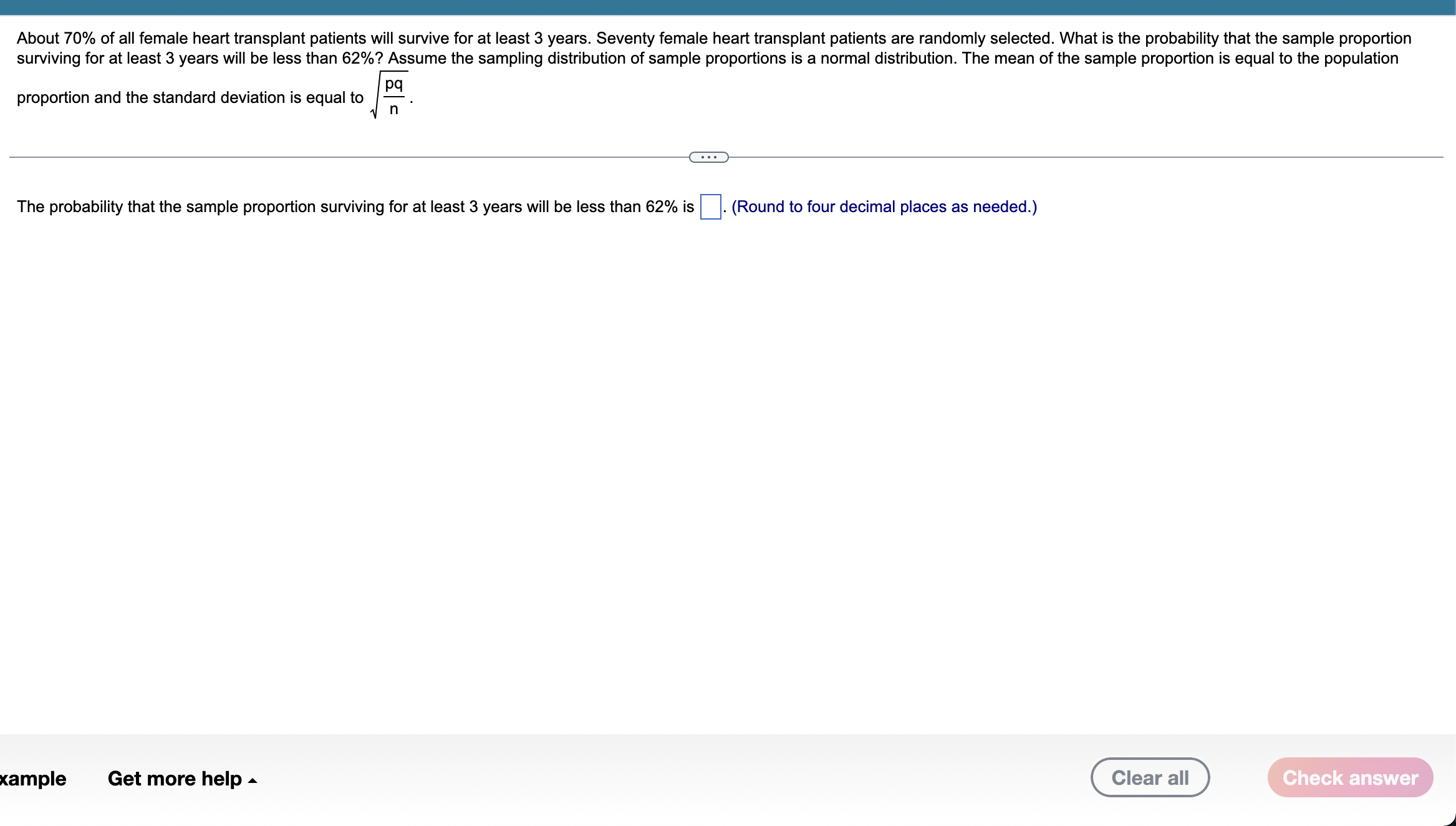
The weights of ice cream cartons are normally distributed with a mean weight of 7 ounces and a standard deviation of 0.5 ounce. (a) What is the probability that a randomly selected carton has a weight greater than 7.17 ounces? (b) A sample of 25 cartons is randomly selected. What is the probability that their mean weight is greater than 7.17 ounces? (a) The probability is 0.3669 (Round to four decimal places as needed.) (b) The probability is (Round to four decimal places as needed.) About 70% of all female heart transplant patients will survive for at least 3 years. Seventy female heart transplant patients are randomly selected. What is the probability that the sample proportion surviving for at least 3 years will be less than 62%? Assume the sampling distribution of sample proportions is a normal distribution. The mean of the sample proportion is equal to the population proportion and the standard deviation is equal to pq n The probability that the sample proportion surviving for at least 3 years will be less than 62% is . (Round to four decimal places as needed.) Clear all Check answer xample Get more help Write the binomial probability and the normal probability for the shaded region of the graph. Find the value of each probability and compare the results. ... AP(x) 0.24- 0.2- n=16 p=0.6 0.16- 0.12- 0.08- 0.04- 0 2 4 6 8 Write the binomial probability for the shaded region of the graph and find its value. Select the correct choice below and fill in the answer box within your choice. (Round to four decimal places as needed.) A. P(6