The worksheet Data1 of the Excel file CentralEnglandTemp2017 shows the 816 monthly mean (surface air) temperatures for the Midlands region of England between 1950 and 2017. (The shown temperatures are in Celsius degrees measured with a precision of 0.1 C.).

It is quite obvious that the monthly temperatures for Midlands must have a seasonal pattern. But do they have a trend?

Define 12 dummy variables corresponding to 12 months (Jan, Feb,, Dec). Since the categorical variable Month has 12 levels (categories), delete the dummy variable Dec, to assume the regression model with linear trend and seasonality:

,

in which t= time period and is the random error term; see the worksheet Data2. Explain why the dummy variable Dec could be deleted.

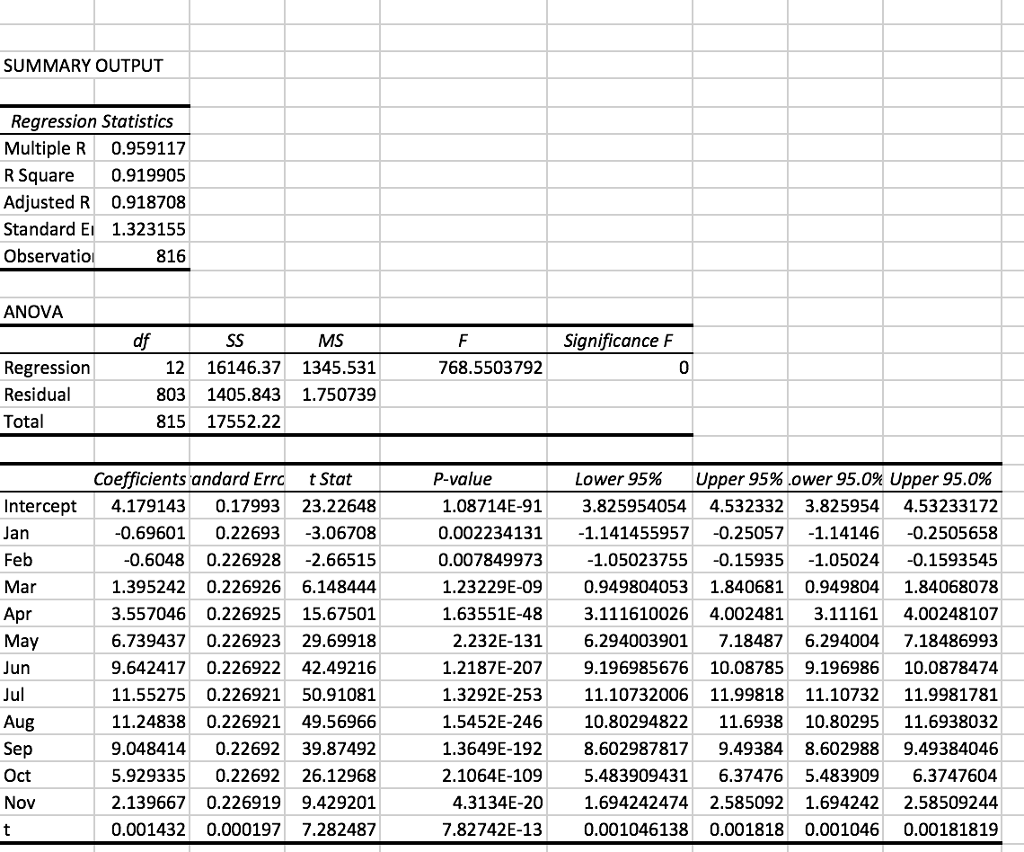
Run Regression in Data Analysis of Excel on the worksheet Data2 to find the estimated regression equation:

(In the worksheet Data2, the dependent variable is in the range M1:M817, the independent variables are in the range A1:L817, and do not forget about checking Labels.) Analyze to conclude which month is typically the coldest and which one is the warmest.

You should know that, in the estimated regression equation found in Task 1, the coefficient is the estimated change (increase or decrease) in the average temperature per month. What is the estimated change in the average temperature per year? (Hint. 1 year has 12 months.) What is the estimated change in the average temperature over 100 years?

Using the estimated regression equation found in Task 1, make forecasts for the twelve months of 2018. (Of course, assume t= 817, 818,, 828, respectively, in making these twelve forecasts, and show details of your calculations.) On the website www.metoffice.gov.uk/hadobs/hadcet/cet_info_mean.html, find the actual mean monthly temperatures (CET) recorded for the first nine months of 2018, and compare them with your forecasts by calculating the nine forecast errors. How many of these errors are positive and how many negative? Knowing that February and March of 2018 were exceptionally cold in the entire Western Europe, how this fact is reflected by your February and March 2018 errors?

Interpret your findings in light of the discussion about global warming. Please, feel free to express your opinion.

Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	t	Temp
1	0	0	0	0	0	0	0	0	0	0	1	4.2
0	1	0	0	0	0	0	0	0	0	0	2	5.3
0	0	1	0	0	0	0	0	0	0	0	3	7.4
0	0	0	1	0	0	0	0	0	0	0	4	7.6
0	0	0	0	1	0	0	0	0	0	0	5	11.3
0	0	0	0	0	1	0	0	0	0	0	6	16.2
0	0	0	0	0	0	1	0	0	0	0	7	15.9
0	0	0	0	0	0	0	1	0	0	0	8	15.6
0	0	0	0	0	0	0	0	1	0	0	9	12.9
0	0	0	0	0	0	0	0	0	1	0	10	9.6
0	0	0	0	0	0	0	0	0	0	1	11	5.7
0	0	0	0	0	0	0	0	0	0	0	12	1.2
1	0	0	0	0	0	0	0	0	0	0	13	3.9
0	1	0	0	0	0	0	0	0	0	0	14	3.7
0	0	1	0	0	0	0	0	0	0	0	15	4.1
0	0	0	1	0	0	0	0	0	0	0	16	6.8
0	0	0	0	1	0	0	0	0	0	0	17	10.1
0	0	0	0	0	1	0	0	0	0	0	18	14
0	0	0	0	0	0	1	0	0	0	0	19	16.3
0	0	0	0	0	0	0	1	0	0	0	20	14.8
0	0	0	0	0	0	0	0	1	0	0	21	14.1
0	0	0	0	0	0	0	0	0	1	0	22	9.4
0	0	0	0	0	0	0	0	0	0	1	23	8.5
0	0	0	0	0	0	0	0	0	0	0	24	5.5
1	0	0	0	0	0	0	0	0	0	0	25	2.7
0	1	0	0	0	0	0	0	0	0	0	26	3.4
0	0	1	0	0	0	0	0	0	0	0	27	6.6
0	0	0	1	0	0	0	0	0	0	0	28	9.6
0	0	0	0	1	0	0	0	0	0	0	29	13.4
0	0	0	0	0	1	0	0	0	0	0	30	14.4
0	0	0	0	0	0	1	0	0	0	0	31	16.8
0	0	0	0	0	0	0	1	0	0	0	32	15.8
0	0	0	0	0	0	0	0	1	0	0	33	10.7
0	0	0	0	0	0	0	0	0	1	0	34	8.8
0	0	0	0	0	0	0	0	0	0	1	35	4.2
0	0	0	0	0	0	0	0	0	0	0	36	2.8
1	0	0	0	0	0	0	0	0	0	0	37	3.3
0	1	0	0	0	0	0	0	0	0	0	38	4.3
0	0	1	0	0	0	0	0	0	0	0	39	5.6
0	0	0	1	0	0	0	0	0	0	0	40	7.3
0	0	0	0	1	0	0	0	0	0	0	41	12.6

SUMMARY OUTPUT Regression Statistics Multiple R 0.959117 R Square0.919905 Adjusted R 0.918708 Standard El 1.323155 Observatio 816 ANOVA df MS Significance F Regression Residual Total 12 16146.371345.531 8031405.843 1.750739 81517552.22 768.5503792 0 Coefficients andard Errd tStat P-value Jan Feb Mar Apr May Jun Jul Aug Intercept4.179143 0.1799323.22648 0.69601 0.22693-3.06708 0.6048 0.226928 -2.66515 1.3952420.226926 6.148444 3.557046 0.226925 15.67501 6.739437 0.226923 29.69918 9.64247 0.226922 42.49216 11.55275 0.22692150.91081 11.24838 0.226921 49.56966 9.048414 0.22692 39.87492 5.929335 0.22692 26.12968 2.139667 0.226919 9.429201 0.001432 0.000197 7.282487 Lower 95% Upper 9596.ower 95.0% Upper 95.0% 1.08714E-913.8259540544.532332 3.825954 4.53233172 0.0022341311.1414559570.25057 1.14146 -0.2505658 1.05023755 -0.15935 -1.05024-0.1593545 1.23229E-090.9498040531.840681 0.949804 1.84068078 3.111610026 4.002481 3.11161 4.00248107 2.232E-131 6.2940039017.184876.294004 7.18486993 1.2187E-2079.196985676 10.08785 9.196986 10.0878474 11.10732006 11.99818 11.10732 11.9981781 10.80294822 11.6938 10.8029511.6938032 1.3649E-192 8.602987817 9.49384 8.6029889.49384046 2.1064E-1095.483909431 6.37476 5.483909 6.3747604 4.3134E-201.694242474 2.585092 1.694242 2.58509244 7.82742E-13 0.001046138 0.001818 0.001046 0.00181819 0.007849973 1.63551E-48 1.3292E-253 1.5452E-246 Oct Nov SUMMARY OUTPUT Regression Statistics Multiple R 0.959117 R Square0.919905 Adjusted R 0.918708 Standard El 1.323155 Observatio 816 ANOVA df MS Significance F Regression Residual Total 12 16146.371345.531 8031405.843 1.750739 81517552.22 768.5503792 0 Coefficients andard Errd tStat P-value Jan Feb Mar Apr May Jun Jul Aug Intercept4.179143 0.1799323.22648 0.69601 0.22693-3.06708 0.6048 0.226928 -2.66515 1.3952420.226926 6.148444 3.557046 0.226925 15.67501 6.739437 0.226923 29.69918 9.64247 0.226922 42.49216 11.55275 0.22692150.91081 11.24838 0.226921 49.56966 9.048414 0.22692 39.87492 5.929335 0.22692 26.12968 2.139667 0.226919 9.429201 0.001432 0.000197 7.282487 Lower 95% Upper 9596.ower 95.0% Upper 95.0% 1.08714E-913.8259540544.532332 3.825954 4.53233172 0.0022341311.1414559570.25057 1.14146 -0.2505658 1.05023755 -0.15935 -1.05024-0.1593545 1.23229E-090.9498040531.840681 0.949804 1.84068078 3.111610026 4.002481 3.11161 4.00248107 2.232E-131 6.2940039017.184876.294004 7.18486993 1.2187E-2079.196985676 10.08785 9.196986 10.0878474 11.10732006 11.99818 11.10732 11.9981781 10.80294822 11.6938 10.8029511.6938032 1.3649E-192 8.602987817 9.49384 8.6029889.49384046 2.1064E-1095.483909431 6.37476 5.483909 6.3747604 4.3134E-201.694242474 2.585092 1.694242 2.58509244 7.82742E-13 0.001046138 0.001818 0.001046 0.00181819 0.007849973 1.63551E-48 1.3292E-253 1.5452E-246 Oct Nov