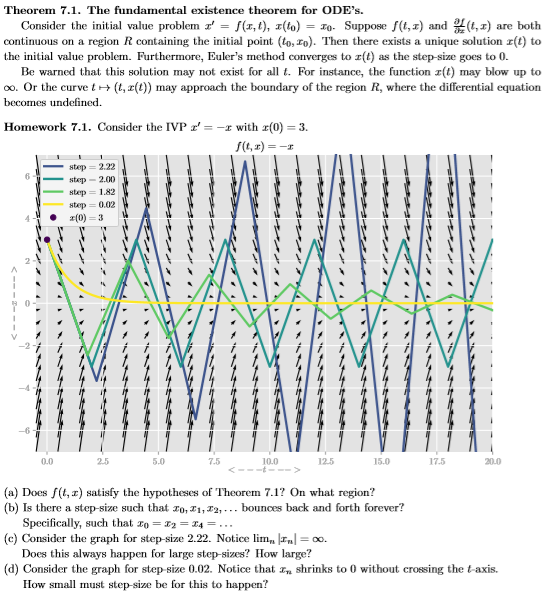
Theorem 7.1. The fundamental existence theorem for ODE's. Consider the initial value problem z' = f(s, t), (to) = 10. Suppose f(t,) and (,) are both continuous on a region R containing the initial point to, to). Then there exists a unique solution r(t) to the initial value problem. Furthermore, Euler's method converges to r(t) as the step-size goes to 0. Be warned that this solution may not exist for all t. For instance, the function (t) may blow up to co. Or the curve t(t, 2()) may approach the boundary of the region R, where the differential equation becomes undefined. Homework 7.1. Consider the IVP Z'= -1 with x(0) = 3. (6) = -1 step2.22 step 2.00 step 1.82 step 0.02 2(0)=3 un 0.0 2.5 5.0 7.5 10.0 12.5 15.0 17.5 200 (a) Does f(t, x) satisfy the hypotheses of Theorem 7.1? On what region? (b) Is there a step-size such that 10, 11, 12,... bounces back and forth forever? Specifically, such that Xo = I2 = 24 =... (c) Consider the graph for step-size 2.22. Notice lim, I = . Does this always happen for large step-sizes? How large? (d) Consider the graph for step size 0.02. Notice that I shrinks to 0 without crossing the taxis. How small must step-size be for this to happen? Theorem 7.1. The fundamental existence theorem for ODE's. Consider the initial value problem z' = f(s, t), (to) = 10. Suppose f(t,) and (,) are both continuous on a region R containing the initial point to, to). Then there exists a unique solution r(t) to the initial value problem. Furthermore, Euler's method converges to r(t) as the step-size goes to 0. Be warned that this solution may not exist for all t. For instance, the function (t) may blow up to co. Or the curve t(t, 2()) may approach the boundary of the region R, where the differential equation becomes undefined. Homework 7.1. Consider the IVP Z'= -1 with x(0) = 3. (6) = -1 step2.22 step 2.00 step 1.82 step 0.02 2(0)=3 un 0.0 2.5 5.0 7.5 10.0 12.5 15.0 17.5 200 (a) Does f(t, x) satisfy the hypotheses of Theorem 7.1? On what region? (b) Is there a step-size such that 10, 11, 12,... bounces back and forth forever? Specifically, such that Xo = I2 = 24 =... (c) Consider the graph for step-size 2.22. Notice lim, I = . Does this always happen for large step-sizes? How large? (d) Consider the graph for step size 0.02. Notice that I shrinks to 0 without crossing the taxis. How small must step-size be for this to happen