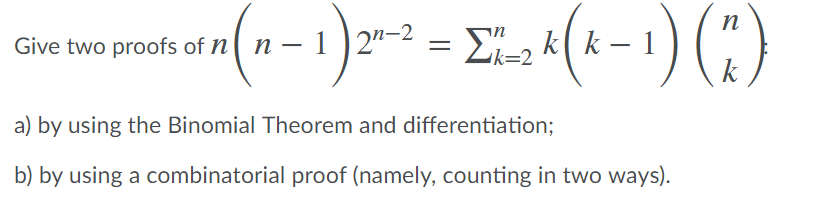
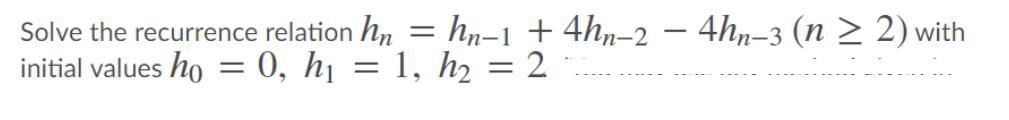
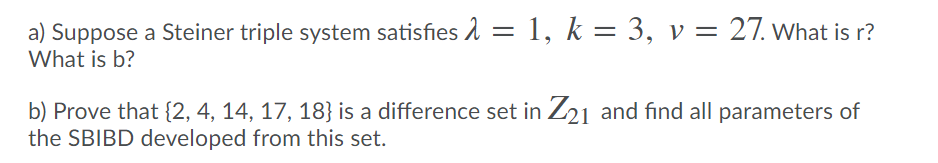
There are 2n people at a party, where n 2 is an integer. Each person has an > even number (possibly zero) of acquaintances. Prove that there are three people at the party with the same number of acquaintances. At a party, eight gentlemen check their hats. In how many ways can their hats be returned so that (a) exactly two of the gentlemen receives their own hats? (b) at least two of the gentlemen receives their own hats? (c) at most two of the gentlemen receives their own hats? n n-12-2 = k Give two proofs of (-1) 2-2LA (A-1) (") (*-1) k=2 a) by using the Binomial Theorem and differentiation; b) by using a combinatorial proof (namely, counting in two ways). Three couples sit at a round table. For some reason, each couple must not sit together. How many ways can this be done? Hint: use the Inclusion-Exclusion Principle. Solve the recurrence relation h = hn1 + 4hn-2 - 4hn-3 (n 2) with initial values ho = 0, h = 1, h2 = 2 Let hn be the number of bags of fruit of apples, oranges, bananas, and pears, in which there are an even number of apples, at most three oranges, a multiple of four number of bananas, and at most one pear. a) Determine the generating function for hn. b) Find a formula for h from the generating function. a) Suppose a Steiner triple system satisfies = 1, k = 3, v = 27. What is r? What is b? b) Prove that {2, 4, 14, 17, 18} is a difference set in Z21 and find all parameters of the SBIBD developed from this set. ( 1 2 3 4 5 6 and C = (R, R, R, B, B, B) Find 4265 2 6 5 13 Letf = alf * c, b)1, c) cycle factorization of f, and d) f4 Use Burnside's theorem to solve the following problems. (You receive little credit if you determine them by examining all possibilities.) a) Determine the number of circular permutations of a multiset S = {R, R, B, B, W, W}. (b) Determine the number of different necklaces that are made up of two red beads, two blue beads, and two white beads.