Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Therefore, the correlation coefficient for our 2 stock portfolio is __________ ? fill in the blanck Below see the detailed calculations of Stock A's Weighted
Therefore, the correlation coefficient for our 2 stock portfolio is __________ ? fill in the blanck 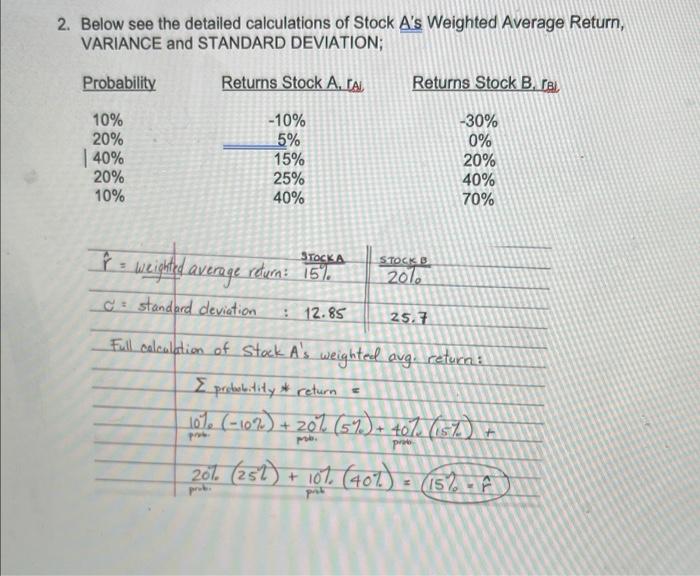

 Below see the detailed calculations of Stock A's Weighted Average Return, VARIANCE and STANDARD DEVIATION; Full calculation of Stack A 's weighted avg. return: probabitity*return=10%(10%)+poo20%(5%)+407(15%)+20%.(252)+10%(40%)=(15%r^) Full Variance Calculation, Stock A Varionce=i=15(rAir^A)=(Probobalityi)r^orAvgReturn=15%.(57.157)2+207=100(201.20.0(157.157.)2401=(407.)(257.157.)2+207.=100(207)=20.0(407.15%)2107.625(107)=62.5VARIANCEZ=165 Full Calculation of COVARIANCE COVAR(AB)i=15(rAir^A)(rBir^B)Probabitityi(rAir^A)(rir^B)Probability(1015)(3020)(101.)=(25)(50)1=125(515)(20)(207)=(10)(20)2=40(1515)(2020)(407.)(0)().4=(2515)(4020)(207)(10)(20)2=40(4015)(7020)(107.)(25)(50)1==(230125) The Standardized measure to express the correlation of stocks' returns is the Correlation Coefficient (see formula below) (A)(B)COVARA,B Full Calculation of COVARIANCE COVAR(AB)=i=15(rAir^A)(rBir^B)Probabitityi(rAir^A)(rir^B)Probability(1015)(3020)(101.)=(25)(50)1=125(515)(20)(207)=(10)(20)2=40(1515)(2020)(407.)(0)()4=(2515)(4020)(207.)(10)(20)2=40(4015)(7020)(107)(25)(50)1=125=330COUARAB The Standardized measure to express the correlation of stocks' returns is the Correlation Coefficient (see formula below) (A)(B)COVARA,B Therefore, the Correlation Coefficient for our 2 stock portfolio is (FILL IN THE BLANK)
Below see the detailed calculations of Stock A's Weighted Average Return, VARIANCE and STANDARD DEVIATION; Full calculation of Stack A 's weighted avg. return: probabitity*return=10%(10%)+poo20%(5%)+407(15%)+20%.(252)+10%(40%)=(15%r^) Full Variance Calculation, Stock A Varionce=i=15(rAir^A)=(Probobalityi)r^orAvgReturn=15%.(57.157)2+207=100(201.20.0(157.157.)2401=(407.)(257.157.)2+207.=100(207)=20.0(407.15%)2107.625(107)=62.5VARIANCEZ=165 Full Calculation of COVARIANCE COVAR(AB)i=15(rAir^A)(rBir^B)Probabitityi(rAir^A)(rir^B)Probability(1015)(3020)(101.)=(25)(50)1=125(515)(20)(207)=(10)(20)2=40(1515)(2020)(407.)(0)().4=(2515)(4020)(207)(10)(20)2=40(4015)(7020)(107.)(25)(50)1==(230125) The Standardized measure to express the correlation of stocks' returns is the Correlation Coefficient (see formula below) (A)(B)COVARA,B Full Calculation of COVARIANCE COVAR(AB)=i=15(rAir^A)(rBir^B)Probabitityi(rAir^A)(rir^B)Probability(1015)(3020)(101.)=(25)(50)1=125(515)(20)(207)=(10)(20)2=40(1515)(2020)(407.)(0)()4=(2515)(4020)(207.)(10)(20)2=40(4015)(7020)(107)(25)(50)1=125=330COUARAB The Standardized measure to express the correlation of stocks' returns is the Correlation Coefficient (see formula below) (A)(B)COVARA,B Therefore, the Correlation Coefficient for our 2 stock portfolio is (FILL IN THE BLANK)



Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


