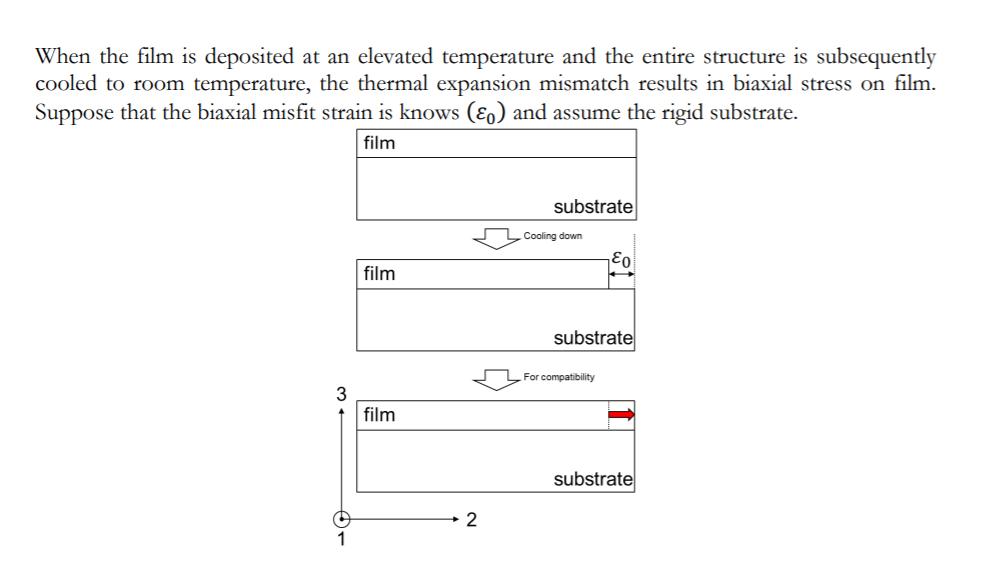
Thin film materials have become technologically important in many engineering applications, such as microelectronics integrated circuits, optical coatings, and wear resistant coating. In this regard, it is important to understand the deformation mechanism in thin film on the thick substrate. Suppose a thin film material is a cubic material which follows the linear elastic constitutive law. [C1111 C1122 1122 0 0 C1122 C1111 C122 0 0 C1122 C1122 C111 0 0 0 0 0 0 0 0 C1212 0 0 0 011) 022 033 023 013 1012/ 0 0 C1212 0 0 0 0 E11 E22 E33 E23 0 0 0 E13 C1212 12/ When the film is deposited at an elevated temperature and the entire structure is subsequently cooled to room temperature, the thermal expansion mismatch results in biaxial stress on film. Suppose that the biaxial misfit strain is knows (o) and assume the rigid substrate. film 3 1 film film 2 substrate Cooling down E0 substrate For compatibility substrate [Hint] The normal stress in the thickness direction is free due to the traction free boundary condition. (a) Express the biaxial stress (6)in terms of stiffness components and the given misfit strain. (b) Using X-ray diffraction, the normal strain in thickness direction could be measured as 33. Express the biaxial strain () and biaxial stress (0) in terms of stiffness components and the measured strain (833). (c) Determine the biaxial modulus B = 0 in terms of stiffness components. Eo Consider the film of which (111) plane parallel to the plane of film. To find relations between stresses and strains in this orientation, we could consider a new coordinate system, as shown below. e = [2, -1,-1], e = Film 3' 1' 1 [0,1,1], e3 = [1,1,1] 3 2' substrate The strain state in the film is given in the new coordinate system as E1/11 = E2121= Eo, E3131 = E * (d) Express the stiffness components C2/2/2/2/ and C2/2/3/3, by performing the 4th rank tensor transformation.