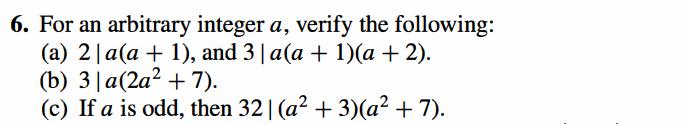4. For n > 1, use mathematical induction to establish each of the following divisibility statements: (a) 8|52n + 7. [Hint: 52k+1) + 7 = 52(52k + 7) + (7 52 . 7).] (b) 15|24" 1. (c) 5|33n+1 + 2"+1. (d) 21|4"+1 + 52n-1. (e) 24 |2.7" + 3. 5" - 5. 6. For an arbitrary integer a, verify the following: (a) 2| a(a + 1), and 3| a(a + 1)(a + 2). (b) 3|a(2a? + 7). (c) If a is odd, then 32| (a2 + 3)(a + 7). 7. For n > 1, verify that 2n + 1 12 + 32 + 52 + ...+ (2n 1) : |