this is a bit long, but all help would be appreciated!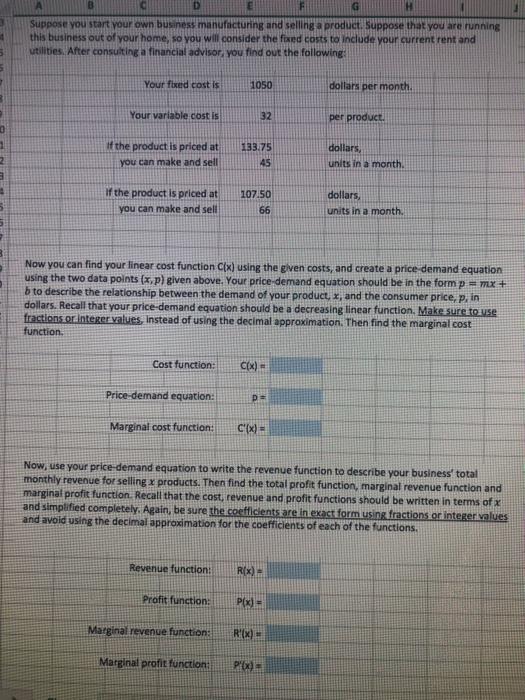

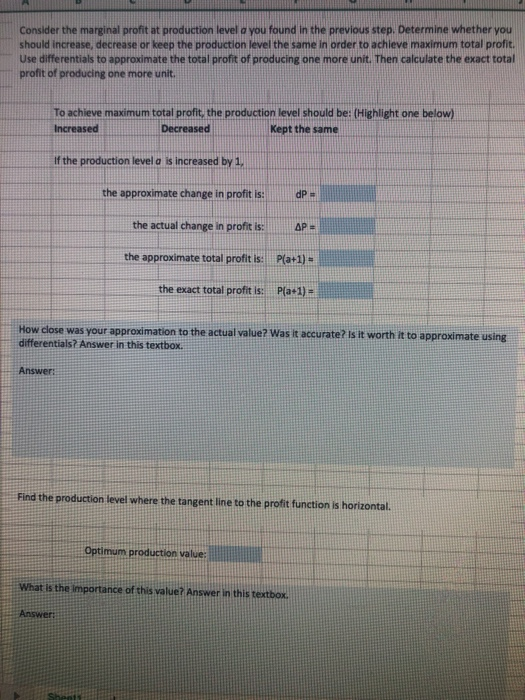
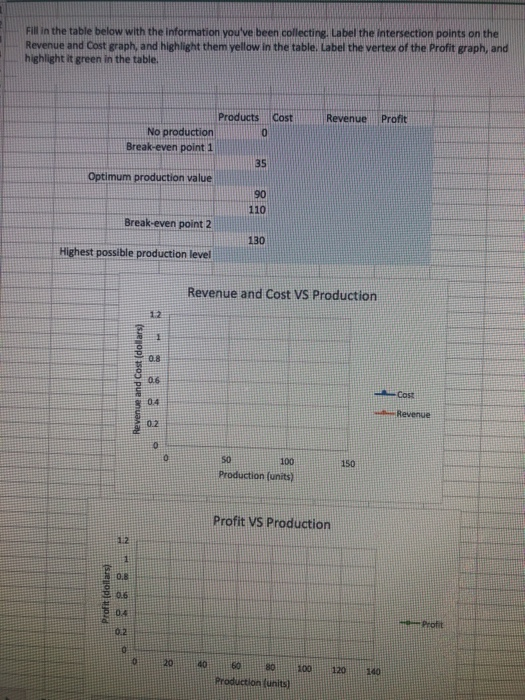
3 A B D G H Suppose you start your own business manufacturing and selling a product. Suppose that you are running this business out of your home, so you will consider the fixed costs to include your current rent and utilities. After consulting a financial advisor, you find out the following: in 5 Your fixed cost is 1050 dollars per month Your variable cost is 32 per product. If the product is priced at you can make and sell 133.75 45 2 3 dollars, units in a month. 11 If the product is priced at you can make and sell 107.50 66 dollars, units in a month. 5 Now you can find your linear cost function Cix) using the given costs, and create a price demand equation using the two data points (x,p) given above. Your price demand equation should be in the form p = mx + b to describe the relationship between the demand of your product, X, and the consumer price, p, in dollars. Recall that your price-demand equation should be a decreasing linear function. Make sure to use fractions or integer values, instead of using the decimal approximation. Then find the marginal cost function Cost function: Cx2) Price-demand equation: Marginal cost function: C'(x) = Now, use your price-demand equation to write the revenue function to describe your business' total monthly revenue for selling x products. Then find the total profit function, marginal revenue function and marginal profit function. Recall that the cost, revenue and profit functions should be written in terms of x and simplified completely. Again, be sure the coefficients are in exact form using fractions or integer values and avoid using the decimal approximation for the coefficients of each of the functions, Revenue function: R(x) Profit function: P(x) Marginal revenue function: R'(X) Marginal profit function: PO) Using your price-demand equation, determine the highest possible production level. Find the x-coordinates of the break-even points using an exact expression (for example, type =SQRT(2) instead of 1.41). Highest possible production level: Break-even point 1: Break-even point 2: What range of production levels should you choose to make a profit? Answer in this textbox. Answer: Reflect back to the two pairs of data that you used to write your price-demand equation, and realize that both demand values fall in the range you found above. Choose one of the two demand values. (Let a = the demand value you choose.) Now suppose your current monthly production level is a units. Then determine the total cost, revenue and profit at this production level and find the marginal cost, revenue, and profit at this production level a. At production level a Total cost: Marginal cost: Total revenue: Marginal revenue: Total profit: Marginal profit: Write a few sentences to interpret the six values above. Answer in this textbox. Answer: Consider the marginal profit at production level a you found in the previous step. Determine whether you should increase, decrease or keep the production level the same in order to achieve maximum total profit. Use differentials to approximate the total profit of producing one more unit. Then calculate the exact total profit of producing one more unit To achieve maximum total profit, the production level should be: (Highlight one below) Increased Decreased Kept the same If the production level a is increased by 1, the approximate change in profit is: dP the actual change in profit is: = the approximate total profit is: Pla+1) the exact total profit is: Pla+1) - How close was your approximation to the actual value? Was it accurate? Is it worth it to approximate using differentials? Answer in this textbox. Answer: Find the production level where the tangent line to the profit function is horizontal. Optimum production value: What is the importance of this value? Answer in this textbox. Answer Sheet Fill in the table below with the information you've been collecting. Label the intersection points on the Revenue and cost graph, and highlight them yellow in the table. Label the vertex of the Profit graph, and highlight it green in the table, Products Cost Revenue Profit 0 No production Break-even point 1 35 Optimum production value 90 110 Break-even point 2 130 Highest possible production level Revenue and Cost VS Production 2 1 0.8 Revenue and Cost (dollars) 06 Cost 04 Revenue 0.2 0 150 50 100 Production (units) Profit VS Production OB Profit (dollars) 0.6 04 Profit 0.2 20 10 100 120 60 80 Production (units) 140 3 A B D G H Suppose you start your own business manufacturing and selling a product. Suppose that you are running this business out of your home, so you will consider the fixed costs to include your current rent and utilities. After consulting a financial advisor, you find out the following: in 5 Your fixed cost is 1050 dollars per month Your variable cost is 32 per product. If the product is priced at you can make and sell 133.75 45 2 3 dollars, units in a month. 11 If the product is priced at you can make and sell 107.50 66 dollars, units in a month. 5 Now you can find your linear cost function Cix) using the given costs, and create a price demand equation using the two data points (x,p) given above. Your price demand equation should be in the form p = mx + b to describe the relationship between the demand of your product, X, and the consumer price, p, in dollars. Recall that your price-demand equation should be a decreasing linear function. Make sure to use fractions or integer values, instead of using the decimal approximation. Then find the marginal cost function Cost function: Cx2) Price-demand equation: Marginal cost function: C'(x) = Now, use your price-demand equation to write the revenue function to describe your business' total monthly revenue for selling x products. Then find the total profit function, marginal revenue function and marginal profit function. Recall that the cost, revenue and profit functions should be written in terms of x and simplified completely. Again, be sure the coefficients are in exact form using fractions or integer values and avoid using the decimal approximation for the coefficients of each of the functions, Revenue function: R(x) Profit function: P(x) Marginal revenue function: R'(X) Marginal profit function: PO) Using your price-demand equation, determine the highest possible production level. Find the x-coordinates of the break-even points using an exact expression (for example, type =SQRT(2) instead of 1.41). Highest possible production level: Break-even point 1: Break-even point 2: What range of production levels should you choose to make a profit? Answer in this textbox. Answer: Reflect back to the two pairs of data that you used to write your price-demand equation, and realize that both demand values fall in the range you found above. Choose one of the two demand values. (Let a = the demand value you choose.) Now suppose your current monthly production level is a units. Then determine the total cost, revenue and profit at this production level and find the marginal cost, revenue, and profit at this production level a. At production level a Total cost: Marginal cost: Total revenue: Marginal revenue: Total profit: Marginal profit: Write a few sentences to interpret the six values above. Answer in this textbox. Answer: Consider the marginal profit at production level a you found in the previous step. Determine whether you should increase, decrease or keep the production level the same in order to achieve maximum total profit. Use differentials to approximate the total profit of producing one more unit. Then calculate the exact total profit of producing one more unit To achieve maximum total profit, the production level should be: (Highlight one below) Increased Decreased Kept the same If the production level a is increased by 1, the approximate change in profit is: dP the actual change in profit is: = the approximate total profit is: Pla+1) the exact total profit is: Pla+1) - How close was your approximation to the actual value? Was it accurate? Is it worth it to approximate using differentials? Answer in this textbox. Answer: Find the production level where the tangent line to the profit function is horizontal. Optimum production value: What is the importance of this value? Answer in this textbox. Answer Sheet Fill in the table below with the information you've been collecting. Label the intersection points on the Revenue and cost graph, and highlight them yellow in the table. Label the vertex of the Profit graph, and highlight it green in the table, Products Cost Revenue Profit 0 No production Break-even point 1 35 Optimum production value 90 110 Break-even point 2 130 Highest possible production level Revenue and Cost VS Production 2 1 0.8 Revenue and Cost (dollars) 06 Cost 04 Revenue 0.2 0 150 50 100 Production (units) Profit VS Production OB Profit (dollars) 0.6 04 Profit 0.2 20 10 100 120 60 80 Production (units) 140