This is a C++ project that I'm currently having problems with. I can't seem to get the loop would anyone be willing to show the code how to do this?

Definition 1. The square root of a number n, denoted n, is a number s whose square is equal to n; that is, if s 2 = n the s is the square root of n. There is an elementary algorithm used to find the square root of a number that takes advantage of a mathematical principle commonly referred to as the pinching (a.k.a. squeezing or sandwich) theorem. The theorem simply means that given any closed continuous interval [a, b], there is a number p such that a p b. We can easily show that such a number,p, exists. a+b 2 , the midpoint between a and b, satisfies the inequality. How does this relate to our square root algorithm? The square root of any number lies in a continous interval between two numbers. We know that n is between 0 and 1 if n is less than 1 and between 1 and n if n is greater than or equal to 1. We would like to keep narrowing, squeezing, the initial interval to obtain better and better approximations of n. We can terminate the algorithm when our approximation is within some predetermined tolerance

To obtain a square of a number, multiply the number by itself. Avoid the use of unnecessary variables. Do not calculate the same quantity more than once - save the calculated value to memory and retrieve it from memory when it is needed. If a calculated quantity is used only once in the program, do not save it to a variable. Declare a constant EPSILON with the value 1E-10 for in your program. That value of gives a square root within ten billionth of the exact square Duncan 2 Fall 2018 COPYRIGHT Classifying Triangles CSc 1253: Programming Project # 1 root. Avoid the use and evaluation of Boolean expressions that are not needed in determining the square root a number. The output should be as shown in the sample run. Each quantity in the table should be right aligned in five-column format and displayed to the nearest hundred millionths place, eight decimal digits. Use a width of twenty for each column. I suggest that you write the program incrementally:

Preliminary Version : Write the program so that it reads a number and displays its square root is NAN if the number is negative or the initial interval, values of low and high, if the number is non-negative. For example, when the input is -36.5, the output is sqrt(-36.500000) nan, when the input is 0.5, the output is low = 0.00000000 high = 1.00000000, and when the input is 25, the output is low = 1.00000000 high = 25.00000000. Ensure that your program produces the correct output for negative numbers, non-negative numbers less than 1 and numbers greater than 1. Use the standard C++ cmath library constant NAN for nan.

Intermediate Version : Add a loop to determine the square root of non-negative numbers. Remove the print statement the printed the initial interval. Your program should now print the square root of a non-negative number. For example, when the input is 36.5, the output is sqrt(36.500000) 6.041523 and when the input is 0.5, the output is sqrt(0.500000) 0.707107

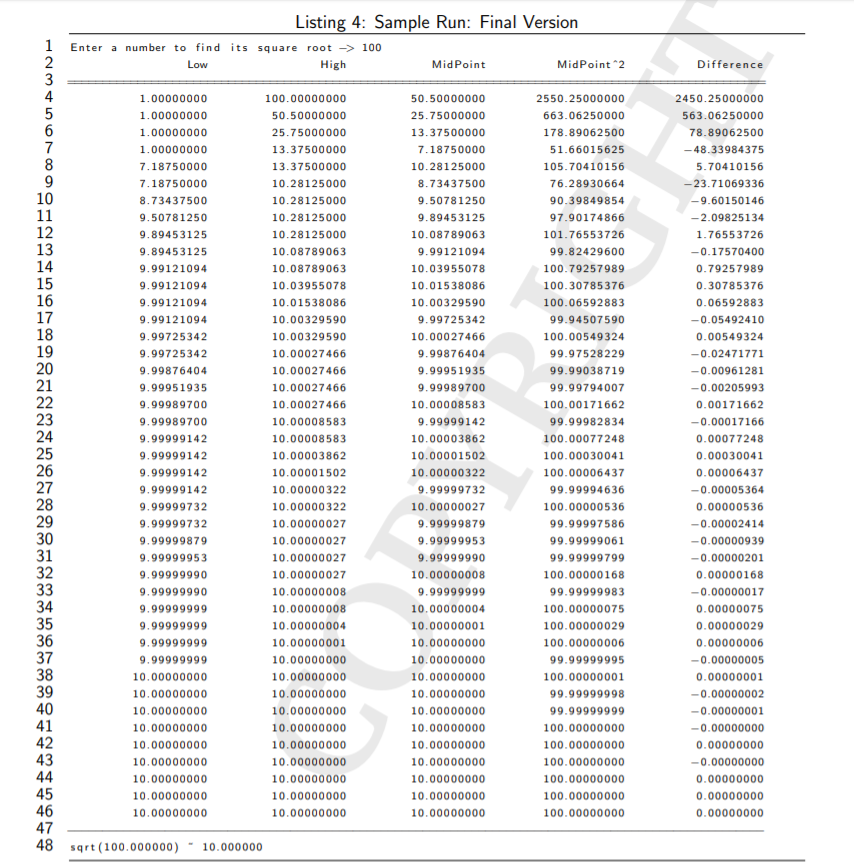
Final Version: Modify the program so that it prints a table as shown in the sample runs whenever the user inputs a non-negative number. The setw, setprecision and right manipulators may come in handy when generating the table.

Listing 4: Sample Run: Final Version Enter a number to find its square root100 Low 1.00000000 1.00000000 1.00000000 1.00000000 100.00000000 50.50000000 25.75000000 13.37500000 13.37500000 10.28125000 10.28125000 10.28125000 10.28125000 50.50000000 25.75000000 13.37500000 7.18750000 10.28125000 2550.25000000 663.06250000 178.89062500 2450.25000000 563.06250000 78.89062500 7 76.28930664 -23.71069336 0781250 9.60150146 -2.09825134 10.08789063 101.76553726 0.175704 0.79257989 0.30785376 10.0878906 10.03955078 10.01538086 10.00329590 10.00329590 10.03955078 10.01538086 10.00329590 100.79257989 100.30785376 100.06592883 100.00549324 0.02471771 -0.00961281 99.97528229 9.99989700 0.00205993 10.00008583 100.00171662 99.99982834 100.00077248 100.00030041 100.00006437 10.00008583 10.0000858 10.00003862 10.00001502 10.00000322 10.00000322 10.00000027 10.00000027 10.00000027 10.00000027 10.00000008 10.00000008 10.00000004 10.00000001 10.00000000 10.00003862 0.00030041 0.00006437 10.00000322 100.00000536 0.00000536 0.00002414 -0.00000939 -0.00000201 0.00000168 -0.00000017 0.00000075 0.00000029 0.00000006 0.00000005 0.00000001 0.00000002 0.00000001 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 10.00000027 9.9999987 9.99999953 99.99999061 10.00000008 9.99999999 10.00000004 10.00000001 10.00000000 0.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 100.00000168 99.99999983 100.00000075 100.00000029 100.00000006 99.99999995 100.00000001 99.99999998 99.99999999 100.00000000 100.00000000 100.00000000 100.00000000 100.00000000 100.00000000 10.00000000 10.00000000 10.00000000 0.00000000 0.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000000 10.00000 10.00000000 48 sqrt (100.000000) 10.000000