Question
This is a .ipynb file, please fill out the AMC(S0,K,r,sigma, N_sim, T, dt, N_basis=6) function based on the instruction (coding base question, European Put price
This is a .ipynb file, please fill out the AMC(S0,K,r,sigma, N_sim, T, dt, N_basis=6) function based on the instruction (coding base question, European Put price for comparison part is only for reference):
Use Monte Carlo to Price American Options (Instructions)
In this homework you will implement your own option pricer using American Monte Carlo (Monte Carlo + Regression) Based on the method prescribed by Longstaff and Schwartz.
Basic Procedures:
- Step 1: Simulate asset price paths for (),=1,2,..S(ti),i=1,2,..N
- Step 2: Option value can be calculated explicitly for tN: ()=max((),0)pk(tN)=max(KSk(tN),0) for path k;
- Step 3: Set =i=N;
- Step 4: Perform linear regression of ()ertpk(ti) against basis function ((1))=(1)fj(S(ti1))=S(ti1)j
- Step 5: Use the regression coefficients to estimate the continuation value at 1ti1: (1)==0((1))C(ti1)=j=0Jjifj(S(ti1))
- Step 6: Set option value (1)=max(max((1),0),(1))pk(ti1)=max(max(KSk(ti1),0),Ck(ti1))
- Step 7: If >1i>1, Set =1i=i1, go back to step 3. Otherwise terminate.
Return option price as the mean of (1)ertpk(t1)
Some code has been provided to you. Your task is to:
- (Mandatory) Fill in the blanks where the code is missing (whereever there is an indication "YOUR CODE HERE")
- Implement the following extension:
- (Mandatory) Try with different number of basis functions (default is 6): 2,3,4,5,6,9,10,20. Plot the option prices against these different orders and write down the observations in your report.
- (Optional) Try to extend the stock simulation model with stochastic volatility (Heston Model), i.e., replace in the equation with a stochastic one: =+dSt=rStdt+VtStdWt, where =()+dVt=(Vt)dt+VtdBt, [,]=d[Wt,Bt]=dt. Modify the pricer accordingly and compare the option price with the constant volatility case.

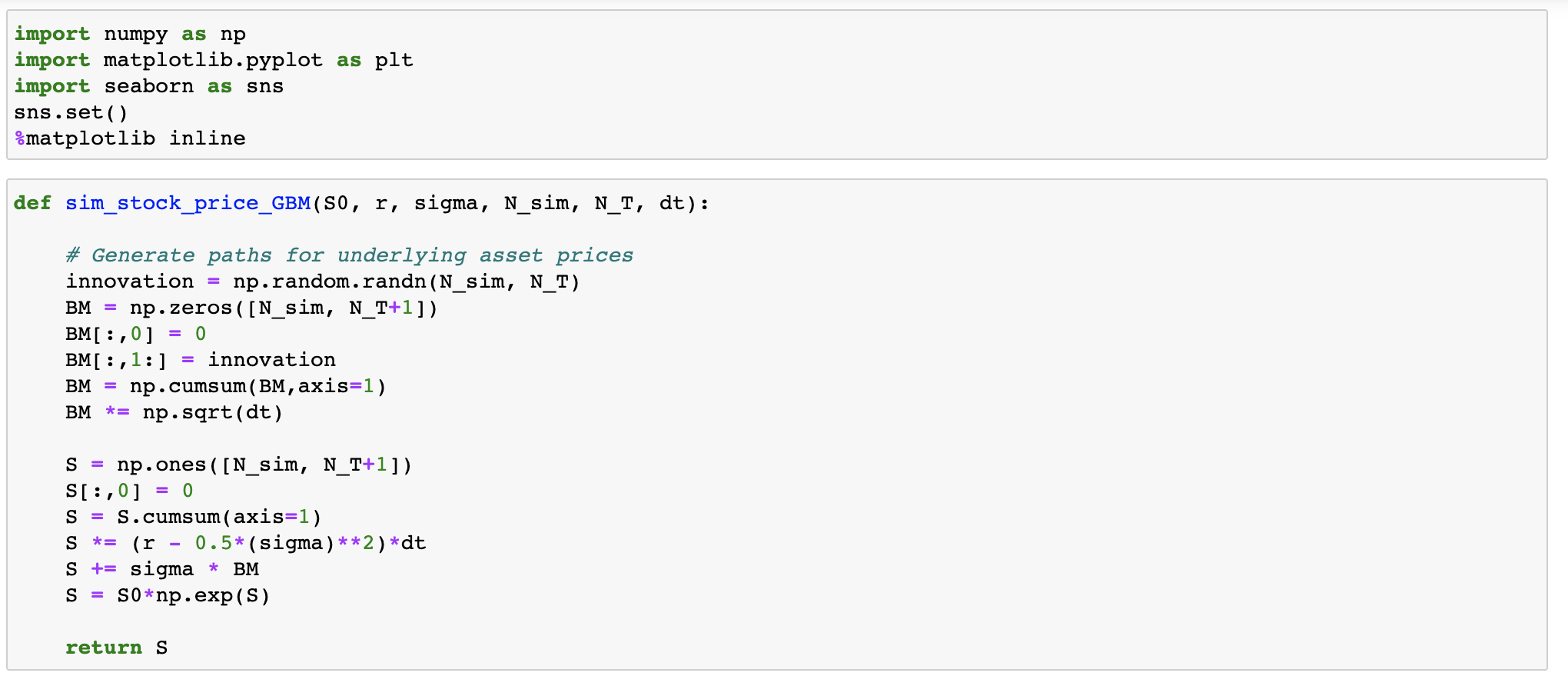

Code for copy:
import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set() %matplotlib inline
def sim_stock_price_GBM(S0, r, sigma, N_sim, N_T, dt): # Generate paths for underlying asset prices innovation = np.random.randn(N_sim, N_T) BM = np.zeros([N_sim, N_T+1]) BM[:,0] = 0 BM[:,1:] = innovation BM = np.cumsum(BM,axis=1) BM *= np.sqrt(dt)
S = np.ones([N_sim, N_T+1]) S[:,0] = 0 S = S.cumsum(axis=1) S *= (r - 0.5*(sigma)**2)*dt S += sigma * BM S = S0*np.exp(S) return S
def AMC(S0,K,r,sigma, N_sim, T, dt, N_basis=6): N_T = int(T/dt) t = np.linspace(0,T,N_T+1)
# Simulate stock prices S= sim_stock_price_GBM(S0, r, sigma, N_sim, N_T,dt) # Now backward induction & regression i = N_T Cont = np.zeros(N_sim) # This stores the continuation value. while i > 1: # First calculate option price p = ... # YOUR CODE HERE x = S[:,i-1] # This is your predictive variable (x). In your prediction you need to use x, x^2, x^3,...x^N, where N = # of basis # discounted option price p_disc = np.exp(-r*dt)*p # This is your target variable (x) reg = ... # YOUR CODE HERE Cont = ...# YOUR CODE HERE i = i - 1 p = ... # YOUR CODE HERE - final option price return np.exp(-r*dt)*np.mean(p)
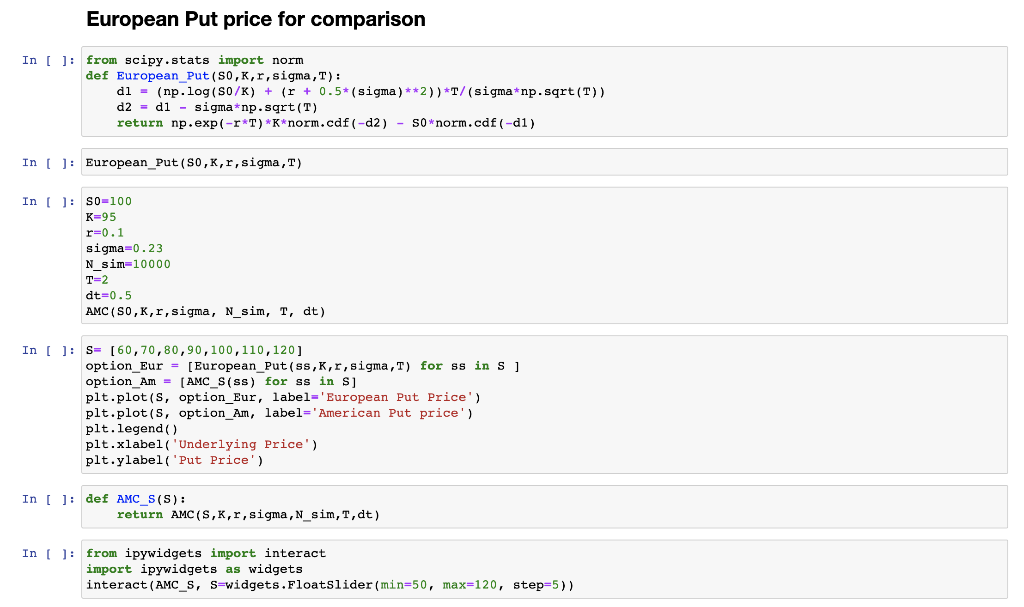
European Put price for comparison
from scipy.stats import norm def European_Put(S0,K,r,sigma,T): d1 = (np.log(S0/K) + (r + 0.5*(sigma)**2))*T/(sigma*np.sqrt(T)) d2 = d1 - sigma*np.sqrt(T) return np.exp(-r*T)*K*norm.cdf(-d2) - S0*norm.cdf(-d1)
European_Put(S0,K,r,sigma,T)
S0=100 K=95 r=0.1 sigma=0.23 N_sim=10000 T=2 dt=0.5 AMC(S0,K,r,sigma, N_sim, T, dt)
S= [60,70,80,90,100,110,120] option_Eur = [European_Put(ss,K,r,sigma,T) for ss in S ] option_Am = [AMC_S(ss) for ss in S] plt.plot(S, option_Eur, label='European Put Price') plt.plot(S, option_Am, label='American Put price') plt.legend() plt.xlabel('Underlying Price') plt.ylabel('Put Price')
def AMC_S(S): return AMC(S,K,r,sigma,N_sim,T,dt)
from ipywidgets import interact import ipywidgets as widgets interact(AMC_S, S=widgets.FloatSlider(min=50, max=120, step=5))
Use Monte Carlo to Price American Options In this homework you will implement your own option pricer using American Monte Carlo (Monte Carlo + Regression) Based on the method prescribed by Longstaff and Schwartz. Basic Procedures: Step 1: Simulate asset price paths for S(ti), i = 1,2,..N Step 2: Option value can be calculated explicitly for tn: P(t) = max(K - S&tn), 0) for path k; Step 3: Set i = N; Step 4: Perform linear regression of er p(t:) against basis function f;(S(t;-1)) = S(t-1) Step 5: Use the regression coefficients to estimate the continuation value at t:-1: C(1:-1) = ;_ B;f;(S(t-1)) Step 6: Set option value x(t-1) = max(max(K Sk(t-1), o), Ck (ti-1)) Step 7: Ifi > 1, Set i = 1 -1, go back to step 3. Otherwise terminate. Return option price as the mean of e-Ap(tu) Some code has been provided to you. Your task is to: 1. (Mandatory) Fill in the blanks where the code is missing (whereever there is an indication "YOUR CODE HERE") 2. Implement the following extension: . (Mandatory) Try with different number of basis functions (default is 6): 2,3,4,5,6,9,10,20. Plot the option prices against these different orders and write down the observations in your report. Optional) Try to extend the stock simulation model with stochastic volatility (Heston Model), i.e., replace o in the equation with a stochastic one: dS= r Sydt + VV,S,DW,, where dV, = (K OV,)dt + n/V,dB,, d[W,, B,] = pdt. Modify the pricer accordingly and compare the option price with the constant volatility case. import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set() %matplotlib inline def sim_stock_price_GBM(S0, r, sigma, N_sim, N_T, dt): # Generate paths for underlying asset prices innovation = np.random.randn(N_sim, N_T) BM = np.zeros( [N_sim, N_T+1]) BM[:,0] 0 BM[:,1:] innovation BM = np.cumsum (BM, axis=1) BM *= np.sqrt(dt) S np.ones ( [N_sim, N_T+1]) S[:,0] 0 S = S.cumsum (axis=1) S *= (r 0.5* (sigma) ** 2) *dt S += sigma * BM S = S0*np.exp(S) return S In [ ]: def AMC (S0,K,r, sigma, N_sim, T, dt, N_basis=6): N_T int(T/dt) t = np.linspace(0,1,N_T+1) 3 # Simulate stock prices S= sim_stock_price_GBM (S0, r, sigma, N_sim, N_T, dt) # Now backward induction & regression i N_T X = Cont = np.zeros (N_sim) # This stores the continuation value. while i > 1: # First calculate option price p = # YOUR CODE HERE S[:,i-1] # This is your predictive variable (x). In your prediction you need to use x, x^2, x^3,...X^N, where N = # # of basis # discounted option price p_disc np.exp(-r*dt) *p # This is your target variable (x) ... # YOUR CODE HERE reg = # YOUR CODE HERE Cont i = i 1 p = # YOUR CODE HERE final option price return np.exp(-r*dt) *np.mean(p) European Put price for comparison In [ ]: from scipy.stats import norm def European_Put (S0,K,r, sigma,T): dl = (np.log(SO/K) + (r + 0.5*(sigma) **2)) *T/(sigma*np.sqrt(T)) d2 = dl - sigma*np.sqrt(T) return np.exp(-1*T)*K* norm.cdf(-d2) - S0*norm.cdf(-d1) In ( ): European_Put (S0,K,r, sigma, T) In ( ): 50-100 K=95 r=0.1 sigma=0.23 N_sim=10000 T-2 dt=0,5 AMC (S0,K,r, sigma, N_sim, T, dt) In [ ]: S= [60,70,80,90,100,110,120] option_Eur = [European_Put (ss,K,1, sigma,T) for ss in S ] option_Am = (AMC_S(SS) for ss in s] plt.plot(s, option_Eur, label='European Put Price') plt.plot(s, option_Am, label='American Put price') plt.legend() plt.xlabel('Underlying Price') plt.ylabel('Put Price') In [ ]: def AMC_S(S): return AMC(S,K,r, sigma, n_sim, T, dt) In [ ]: from ipywidgets import interact import ipywidgets as widgets interact(AMC_S, S=widgets.Floatslider(min=50, max=120, step=5)) Use Monte Carlo to Price American Options In this homework you will implement your own option pricer using American Monte Carlo (Monte Carlo + Regression) Based on the method prescribed by Longstaff and Schwartz. Basic Procedures: Step 1: Simulate asset price paths for S(ti), i = 1,2,..N Step 2: Option value can be calculated explicitly for tn: P(t) = max(K - S&tn), 0) for path k; Step 3: Set i = N; Step 4: Perform linear regression of er p(t:) against basis function f;(S(t;-1)) = S(t-1) Step 5: Use the regression coefficients to estimate the continuation value at t:-1: C(1:-1) = ;_ B;f;(S(t-1)) Step 6: Set option value x(t-1) = max(max(K Sk(t-1), o), Ck (ti-1)) Step 7: Ifi > 1, Set i = 1 -1, go back to step 3. Otherwise terminate. Return option price as the mean of e-Ap(tu) Some code has been provided to you. Your task is to: 1. (Mandatory) Fill in the blanks where the code is missing (whereever there is an indication "YOUR CODE HERE") 2. Implement the following extension: . (Mandatory) Try with different number of basis functions (default is 6): 2,3,4,5,6,9,10,20. Plot the option prices against these different orders and write down the observations in your report. Optional) Try to extend the stock simulation model with stochastic volatility (Heston Model), i.e., replace o in the equation with a stochastic one: dS= r Sydt + VV,S,DW,, where dV, = (K OV,)dt + n/V,dB,, d[W,, B,] = pdt. Modify the pricer accordingly and compare the option price with the constant volatility case. import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set() %matplotlib inline def sim_stock_price_GBM(S0, r, sigma, N_sim, N_T, dt): # Generate paths for underlying asset prices innovation = np.random.randn(N_sim, N_T) BM = np.zeros( [N_sim, N_T+1]) BM[:,0] 0 BM[:,1:] innovation BM = np.cumsum (BM, axis=1) BM *= np.sqrt(dt) S np.ones ( [N_sim, N_T+1]) S[:,0] 0 S = S.cumsum (axis=1) S *= (r 0.5* (sigma) ** 2) *dt S += sigma * BM S = S0*np.exp(S) return S In [ ]: def AMC (S0,K,r, sigma, N_sim, T, dt, N_basis=6): N_T int(T/dt) t = np.linspace(0,1,N_T+1) 3 # Simulate stock prices S= sim_stock_price_GBM (S0, r, sigma, N_sim, N_T, dt) # Now backward induction & regression i N_T X = Cont = np.zeros (N_sim) # This stores the continuation value. while i > 1: # First calculate option price p = # YOUR CODE HERE S[:,i-1] # This is your predictive variable (x). In your prediction you need to use x, x^2, x^3,...X^N, where N = # # of basis # discounted option price p_disc np.exp(-r*dt) *p # This is your target variable (x) ... # YOUR CODE HERE reg = # YOUR CODE HERE Cont i = i 1 p = # YOUR CODE HERE final option price return np.exp(-r*dt) *np.mean(p) European Put price for comparison In [ ]: from scipy.stats import norm def European_Put (S0,K,r, sigma,T): dl = (np.log(SO/K) + (r + 0.5*(sigma) **2)) *T/(sigma*np.sqrt(T)) d2 = dl - sigma*np.sqrt(T) return np.exp(-1*T)*K* norm.cdf(-d2) - S0*norm.cdf(-d1) In ( ): European_Put (S0,K,r, sigma, T) In ( ): 50-100 K=95 r=0.1 sigma=0.23 N_sim=10000 T-2 dt=0,5 AMC (S0,K,r, sigma, N_sim, T, dt) In [ ]: S= [60,70,80,90,100,110,120] option_Eur = [European_Put (ss,K,1, sigma,T) for ss in S ] option_Am = (AMC_S(SS) for ss in s] plt.plot(s, option_Eur, label='European Put Price') plt.plot(s, option_Am, label='American Put price') plt.legend() plt.xlabel('Underlying Price') plt.ylabel('Put Price') In [ ]: def AMC_S(S): return AMC(S,K,r, sigma, n_sim, T, dt) In [ ]: from ipywidgets import interact import ipywidgets as widgets interact(AMC_S, S=widgets.Floatslider(min=50, max=120, step=5))Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


