This is a java problem, I have to write/complete just 3 methods, I need urgent help please cause I'm so confused. I will post the question so you understand but its just 3 methods please. Below is a link to the drive with the package although I typed the code below. The methods I need to coplete are commented "TODO" on them. Thanks please. Its Krusla's algorithm. I have a psueocode if it may help. Just 3 methods please

https://drive.google.com/file/d/15mVL5ud8XHF_L1lQhmd7zfXBomQnO5pq/view?usp=sharing

#Kruskal Class

import lib280.graph.Vertex280;

import lib280.graph.WeightedEdge280;

import lib280.graph.WeightedGraphAdjListRep280;

import lib280.tree.ArrayedMinHeap280;

public class Kruskal {

public static WeightedGraphAdjListRep280 minSpanningTree(WeightedGraphAdjListRep280 G) {

// TODO -- Complete this method.

return null; // Remove this when you're ready -- it is just a placeholder to prevent a compiler error.

}

public static void main(String args[]) {

WeightedGraphAdjListRep280 G = new WeightedGraphAdjListRep280(1, false);

// If you get a file not found error here and you're using eclipse just remove the

// 'Kruskal-template/' part from the path string.

G.initGraphFromFile("Kruskal-template/mst.graph");

System.out.println(G);

WeightedGraphAdjListRep280 minST = minSpanningTree(G);

System.out.println(minST);

}

}

#UnionFind class

import lib280.graph.Edge280;

import lib280.graph.GraphAdjListRep280;

import lib280.graph.Vertex280;

public class UnionFind280 {

GraphAdjListRep280> G;

/**

* Create a new union-find structure.

*

* @param numElements Number of elements (numbered 1 through numElements, inclusive) in the set.

* @postcond The structure is initialized such that each element is in its own subset.

*/

public UnionFind280(int numElements) {

G = new GraphAdjListRep280>(numElements, true);

G.ensureVertices(numElements);

}

/**

* Return the representative element (equivalence class) of a given element.

* @param id The elements whose equivalence class we wish to find.

* @return The representative element (equivalence class) of the element 'id'.

*/

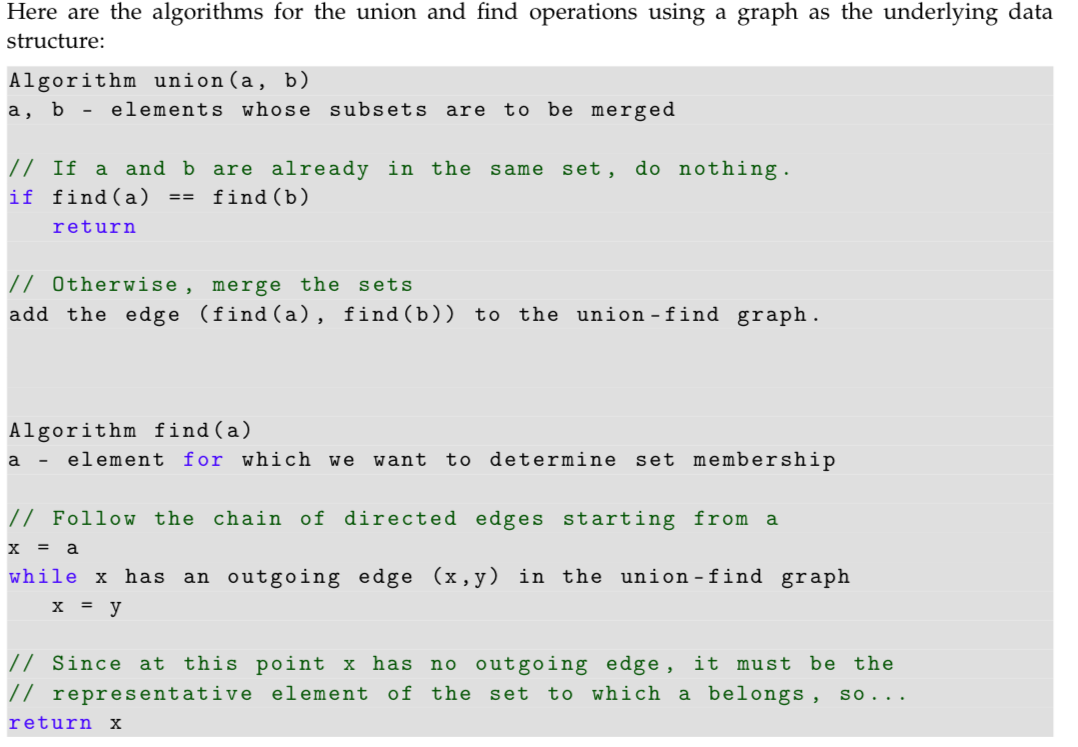
public int find(int id) {

// TODO - Write this method

return 0; // Remove this when you are ready. It is just a placeholder to prevent a compiler error.

}

/**

* Merge the subsets containing two items, id1 and id2, making them, and all of the other elemnets in both sets, "equivalent".

* @param id1 First element.

* @param id2 Second element.

*/

public void union(int id1, int id2) {

// TODO - Write this method.

}

}

Implementation Hints

When implementing Kruskals algorithm, you should be able to avoid having to write your own sorting algorithm, or putting the edges into an array to sort the edges by their weights. You can take advantage of ADTs already in lib280-asn8a. All you need is to put the edges in a dispenser which, when you remove an item, will always give you the edge with the smallest weight (hint: look in the lib280.tree package for ArrayedMinHeap280). Conveniently, WeightedEdge280 objects are Comparable based on their weight.

For this problem you will implement Kruskal's algorithm for tinding the minimum spann?ng tree of an undirected weighted graph. Kruskal's algorithm uses a union-find data structure to keep track of subsets of vertices of the input graph G. Initially, every vertex of G is in a subset by itself. The intuition for Kruskal's algorithm is that the edges of the input graph G are sorted in ascending order of weight (smallest weights first), then each such edge (a, b) is examined in order, and if a and b are currently in different subsets we merge the two sets containing a and b and add (a, b) to the graph of the minimum spanning tree. This works because vertices in the same subset in the union-find structure are all connected. Once all of the vertices are in the same subset, we know that they are all connected. Since we always add the next smallest edge possible to the minimum spanning tree, the result is the smallest-cost set of edges that cause the graph to be completely connected, i.e. the minimum spanning tree! Here's Kruskal's algorithm, in pseudocode: Algoirthm minimumSpanningTreeKruskal (G) A weighted, undirected graph minST - an undirected, weighted graph with the same node set as G, but no edges - a union -find data structure containing the node set of G in which each node is initially in its own subset Sort the edges of G in order from smallest to largest weight for each edge e (a,b) in sorted order if UF.find (a)UF.find (b) minST.addEdge (a, b) set the weight of (a,b) in minST to the weight of (a,b) in G UF.union (a, b) For this problem you will implement Kruskal's algorithm for tinding the minimum spann?ng tree of an undirected weighted graph. Kruskal's algorithm uses a union-find data structure to keep track of subsets of vertices of the input graph G. Initially, every vertex of G is in a subset by itself. The intuition for Kruskal's algorithm is that the edges of the input graph G are sorted in ascending order of weight (smallest weights first), then each such edge (a, b) is examined in order, and if a and b are currently in different subsets we merge the two sets containing a and b and add (a, b) to the graph of the minimum spanning tree. This works because vertices in the same subset in the union-find structure are all connected. Once all of the vertices are in the same subset, we know that they are all connected. Since we always add the next smallest edge possible to the minimum spanning tree, the result is the smallest-cost set of edges that cause the graph to be completely connected, i.e. the minimum spanning tree! Here's Kruskal's algorithm, in pseudocode: Algoirthm minimumSpanningTreeKruskal (G) A weighted, undirected graph minST - an undirected, weighted graph with the same node set as G, but no edges - a union -find data structure containing the node set of G in which each node is initially in its own subset Sort the edges of G in order from smallest to largest weight for each edge e (a,b) in sorted order if UF.find (a)UF.find (b) minST.addEdge (a, b) set the weight of (a,b) in minST to the weight of (a,b) in G UF.union (a, b)