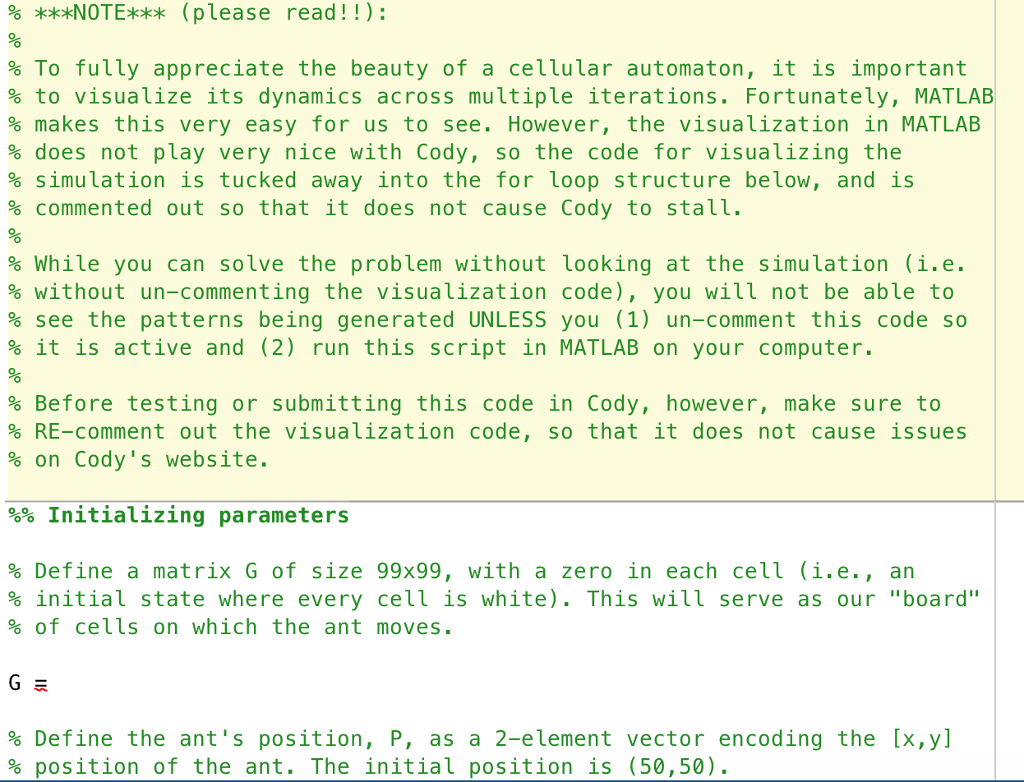
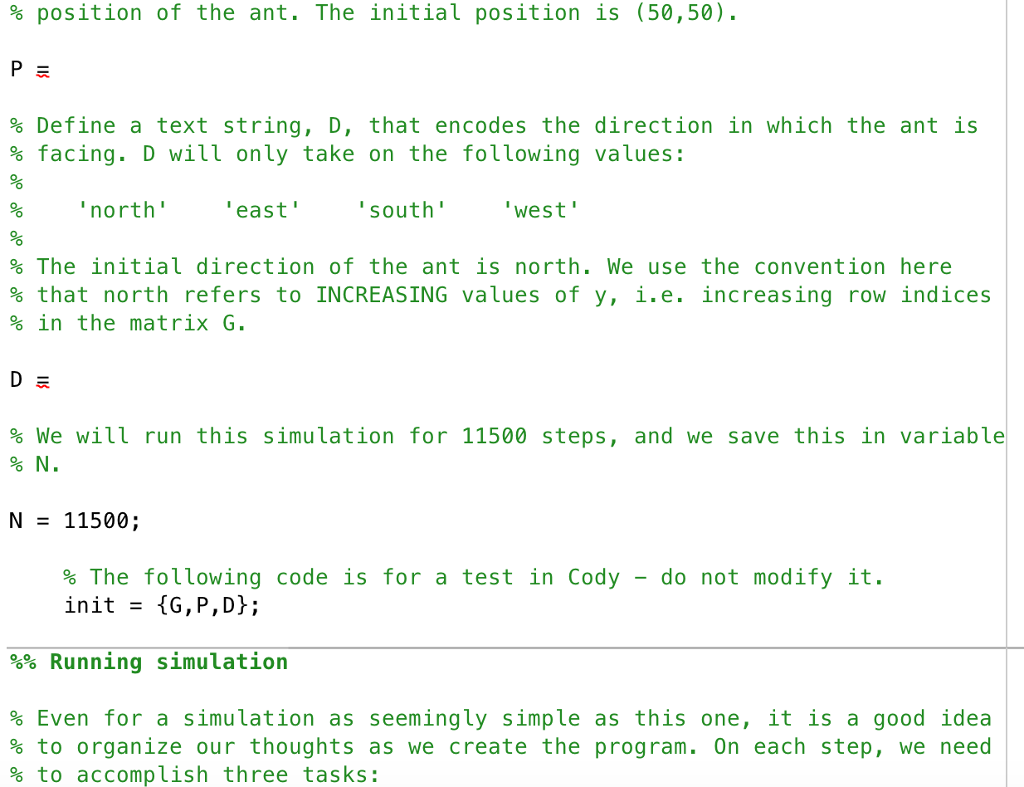
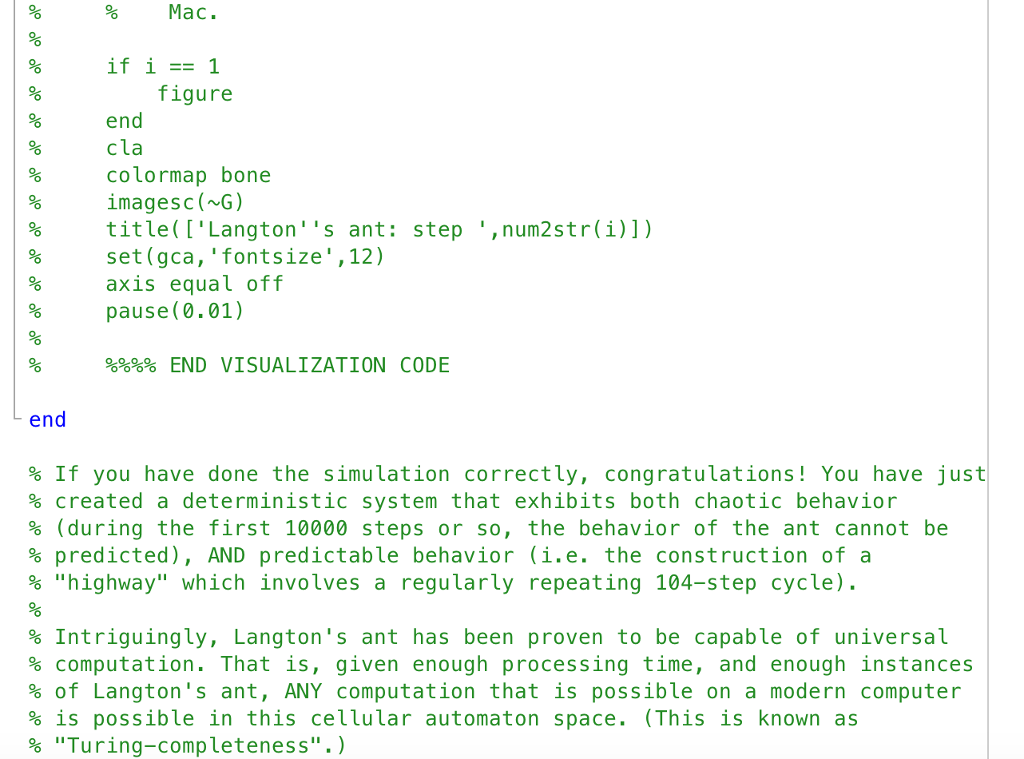
This is a matlab problem(The screen is the correct sequence)

Cellular automata, such as the elementary automaton discussed in class, are discrete models that are used in various fields of mathematics and science. Some of these systems are particularly interesting due to the seemingly unpredictable emergence of pseudorandomness and irregularity, despite the deterministic rules that are used to define them. Cellular automata can be extended to 2 dimensions by defining a regular 2-dimensional grid on which the automaton is defined. Each square in the grid is a cell and can have one of several discrete states. Here, we will investigate a canonical example of a 2- D cellular automaton, Langton's ant. The rules underlying the ant's local movement are trivially simple to explain, but a macroscopic characterization of the ant's movement is far more elusive. A rectangular board of cells is defined with every cell having a initial state of 0, corresponding to the color white. In our simulation, we will use a 99x99 grid. A cell is arbitrarily chosen as the location of the "ant" (we select the position (50, 50) in our simulation). The antis initially facing north, i.e. towards the top of the grid. The simulation takes place in discrete steps. On each step, the ant does one of two things If the ant is standing on a cell with value 0 (a white square), it turns 90 to the right, flips the value to 1 (to black), and moves forward one unit If the ant is standing on a cell with value 1 (a black square), it turns 90 tothe left, flips the value to 0 (to white), and moves forward one unit. Over time, the pattern on the board changes according to these simple rules. To implement Langton's ant in MATLAB, we need to keep track of several variables: the current state of the board, the location of the ant, and the cardinal direction in which the ant is facing (north, east, south, or west). W will also need to program the instruction for the ant to flip a cell's value, and change its cardinal direction based on the cell's value. We will then iterate this procedure a set number of times and observe the dynamics of the board Cellular automata, such as the elementary automaton discussed in class, are discrete models that are used in various fields of mathematics and science. Some of these systems are particularly interesting due to the seemingly unpredictable emergence of pseudorandomness and irregularity, despite the deterministic rules that are used to define them. Cellular automata can be extended to 2 dimensions by defining a regular 2-dimensional grid on which the automaton is defined. Each square in the grid is a cell and can have one of several discrete states. Here, we will investigate a canonical example of a 2- D cellular automaton, Langton's ant. The rules underlying the ant's local movement are trivially simple to explain, but a macroscopic characterization of the ant's movement is far more elusive. A rectangular board of cells is defined with every cell having a initial state of 0, corresponding to the color white. In our simulation, we will use a 99x99 grid. A cell is arbitrarily chosen as the location of the "ant" (we select the position (50, 50) in our simulation). The antis initially facing north, i.e. towards the top of the grid. The simulation takes place in discrete steps. On each step, the ant does one of two things If the ant is standing on a cell with value 0 (a white square), it turns 90 to the right, flips the value to 1 (to black), and moves forward one unit If the ant is standing on a cell with value 1 (a black square), it turns 90 tothe left, flips the value to 0 (to white), and moves forward one unit. Over time, the pattern on the board changes according to these simple rules. To implement Langton's ant in MATLAB, we need to keep track of several variables: the current state of the board, the location of the ant, and the cardinal direction in which the ant is facing (north, east, south, or west). W will also need to program the instruction for the ant to flip a cell's value, and change its cardinal direction based on the cell's value. We will then iterate this procedure a set number of times and observe the dynamics of the board