This is all one question! Drop down selections provided at the bottom. Thank you in advance~

1. sensitivity/scenario
2. stay positive/become negative
3. $5.80/$1.93/$2.66/$1.03 mil
4. $5.30/$7.13/$6.56/$6.16 mil
5. z= -0.65/1.03/-1.09/-0.83
6. 13.79%/26.43%/31.21%/14.46%

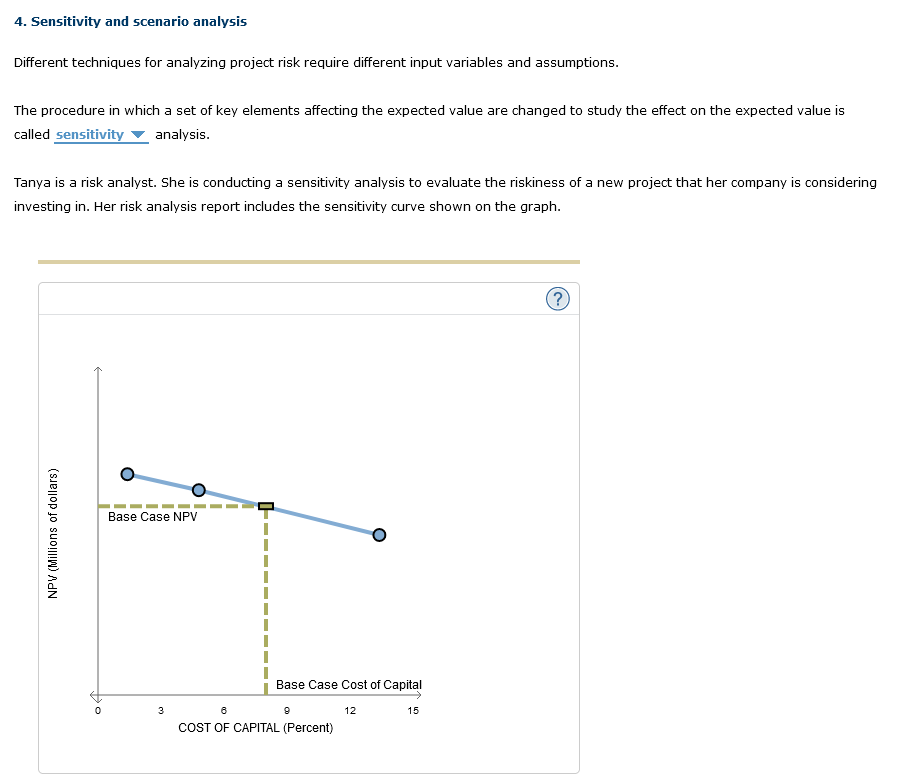
4. Sensitivity and scenario analysis Different techniques for analyzing project risk require different input variables and assumptions. The procedure in which a set of key elements affecting the expected value are changed to study the effect on the expected value is called analysis. Tanya is a risk analyst. She is conducting a sensitivity analysis to evaluate the riskiness of a new project that her company is considering investing in. Her risk analysis report includes the sensitivity curve shown on the graph. This curve implies that the project is not very sensitive to changes in cost of capital. The project's NPV is likely to if the cost of capital increases to 15%. Along with the sensitivity analysis, Tanya is including a scenario analysis for the project in her report, giving the probability of the project generating a negative NPV. Her report includes the following information about the scenario analysis: Complete the missing information in Tanya's report: (Note: Round your answers to two decimal places.) The expected net present value of the project is Standard deviation of the net present value (the NPV of the project is likely to vary by) $ million. Assuming that probability distribution is normal, the value of z is Thus, the project has a chance to generate an NPV of less than $0. 4. Sensitivity and scenario analysis Different techniques for analyzing project risk require different input variables and assumptions. The procedure in which a set of key elements affecting the expected value are changed to study the effect on the expected value is called analysis. Tanya is a risk analyst. She is conducting a sensitivity analysis to evaluate the riskiness of a new project that her company is considering investing in. Her risk analysis report includes the sensitivity curve shown on the graph. This curve implies that the project is not very sensitive to changes in cost of capital. The project's NPV is likely to if the cost of capital increases to 15%. Along with the sensitivity analysis, Tanya is including a scenario analysis for the project in her report, giving the probability of the project generating a negative NPV. Her report includes the following information about the scenario analysis: Complete the missing information in Tanya's report: (Note: Round your answers to two decimal places.) The expected net present value of the project is Standard deviation of the net present value (the NPV of the project is likely to vary by) $ million. Assuming that probability distribution is normal, the value of z is Thus, the project has a chance to generate an NPV of less than $0