This is an exponential density probability problem

the general solution is attached below.

A hard drive has a "decay" parameter of 1/30 since the expected life of the hard drive is 30 months.

a) Compute the probability that the hard drive will break in the first year.

b) Compute the probability that the hard drive will last more than one year. (There are at least two ways you could find this. For the following problems, find this probability by changing the limits of integration.)

c) Compute the probability that the hard drive lasts more than two years.

d) Congratulations, your hard drive survived the first year! What's the probability that it will be OK for one more year, to two years after you bought it? This is not the same question as (c); we now have the additional information that it last the first year. This is a conditional probability; to find it, divide your (c) answer by your (b) answer.

e) Congratulations, your hard drive has survived for 5 years!! What's the probability it will last one more year?

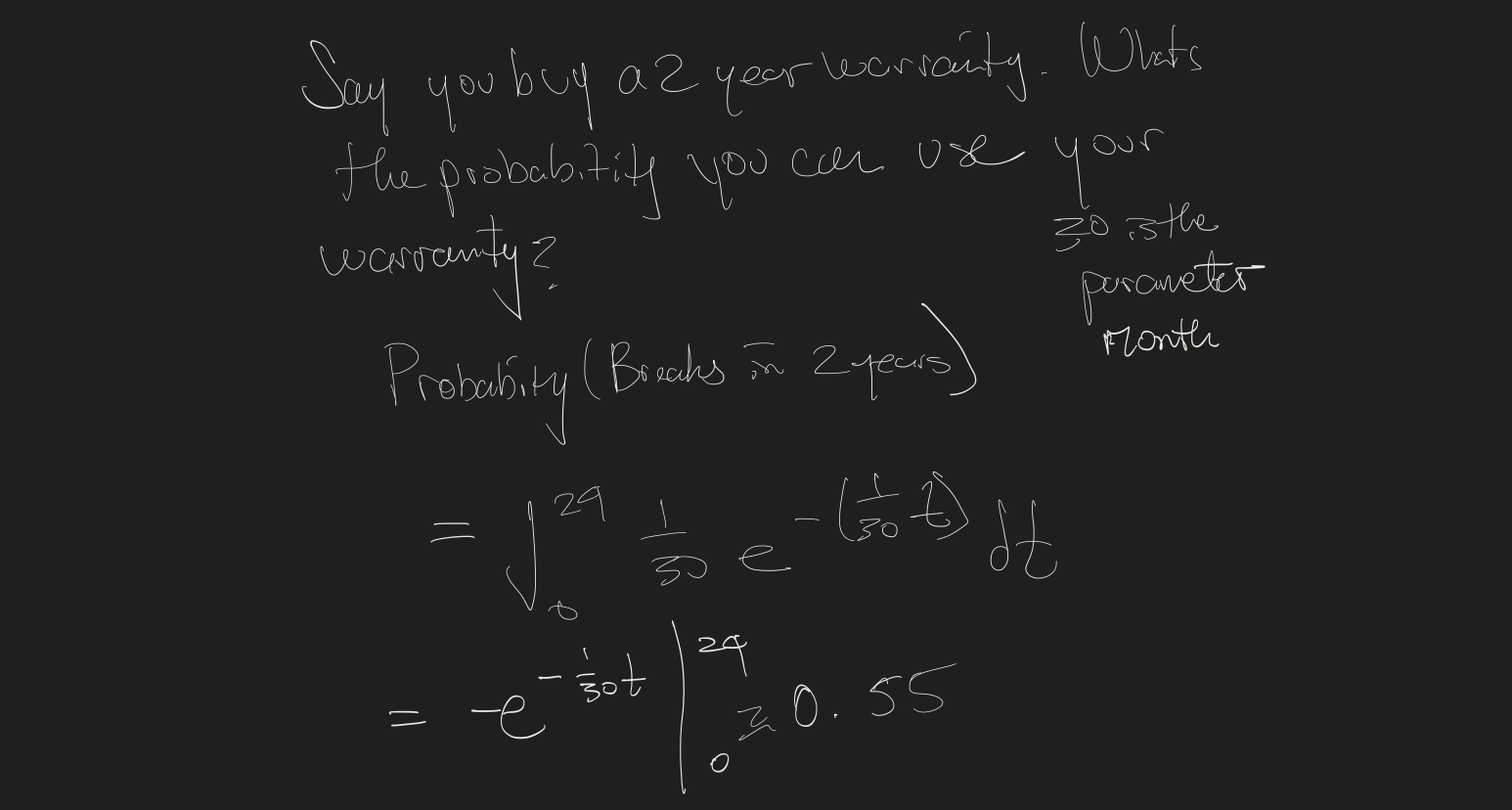
your Say you buy az year warranty. What's the probability you can use warranty? Probabity (Brocks in 2 years) =29 = sot -GDJE 30.55 It 30 is the parameter Month