This is my code and it is implementing a 2 approxiamtion algortihm for the metric Travelling Salesperson problem involving constuctung a minium spanning tree from the given graph and then traversing it in a specific way to generate an approximate hamiltonian cycle. The input file is first sent to a file that makes the graph and then the mst and evyerthing else acceses it as G. I have attached picture of the prompt and weighted_graph.py. I need help debugging because my out put is not correct. PLEASE HELP AND I WILL GIVE THUMBS UP.
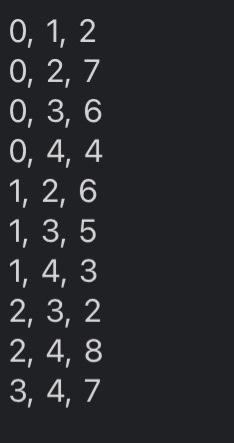
My issue is for example I have this input file.
the Output should be:
Hamiltonian cycle of weight 21:
0, 1, 3, 2, 4, 0
but it is
Hamiltonian cycle of weight 18:
0, 1, 4, 3, 0
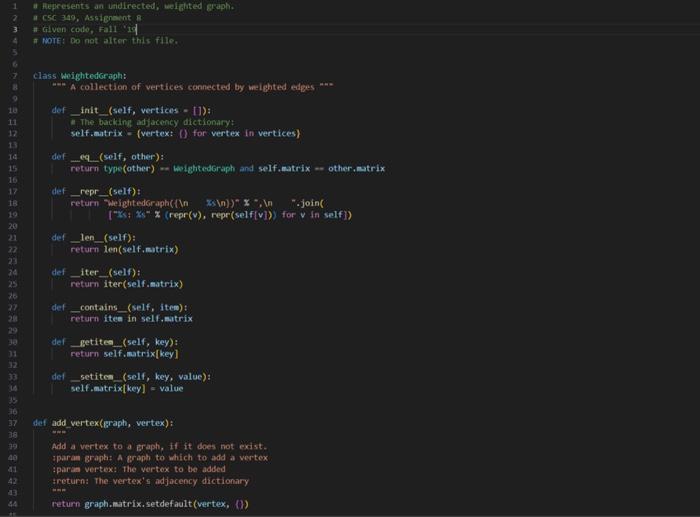
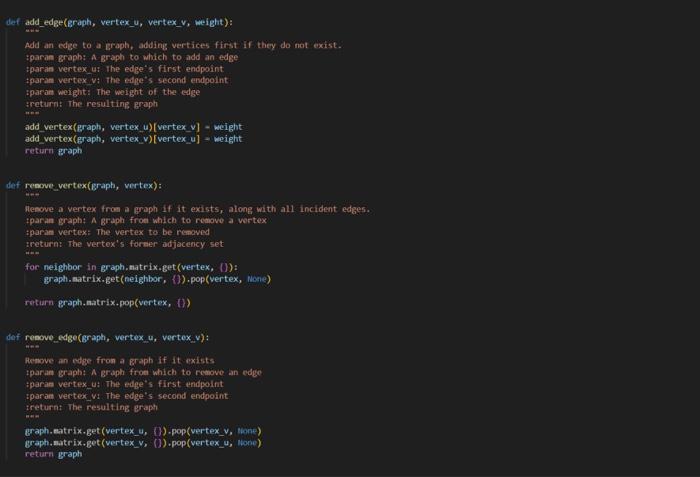
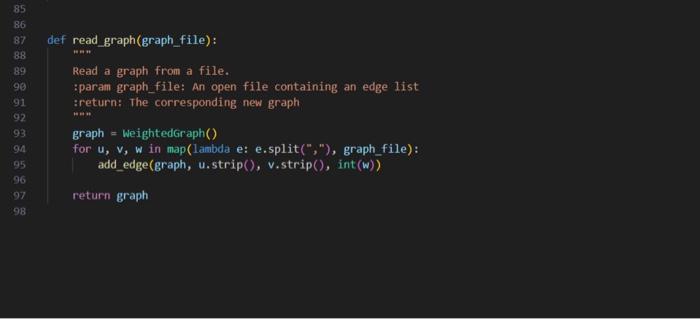
weighted_graph.py
prompt
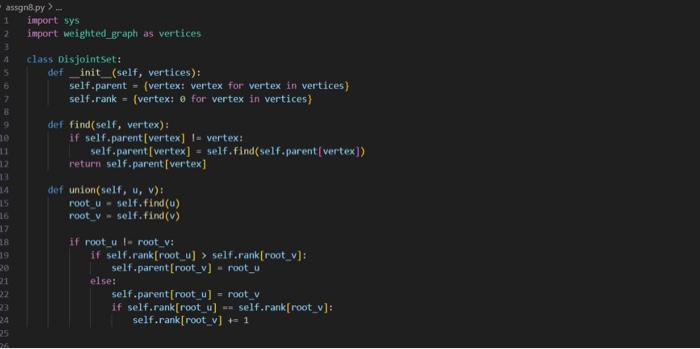
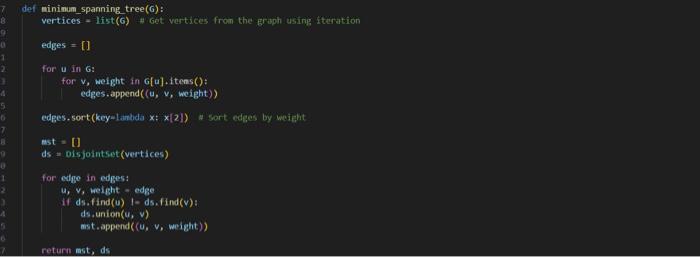
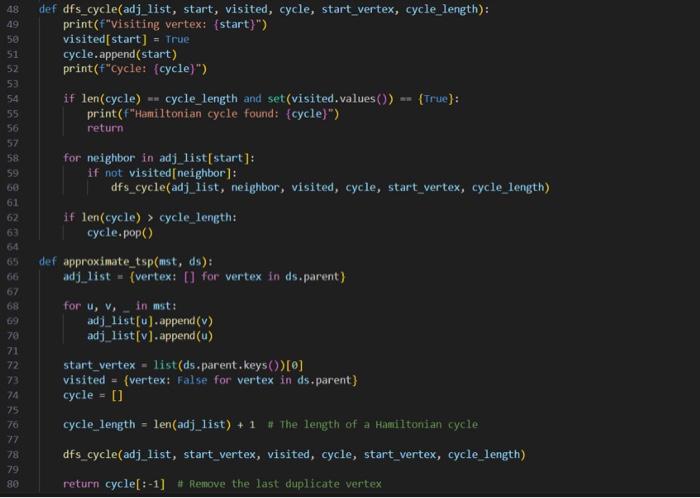
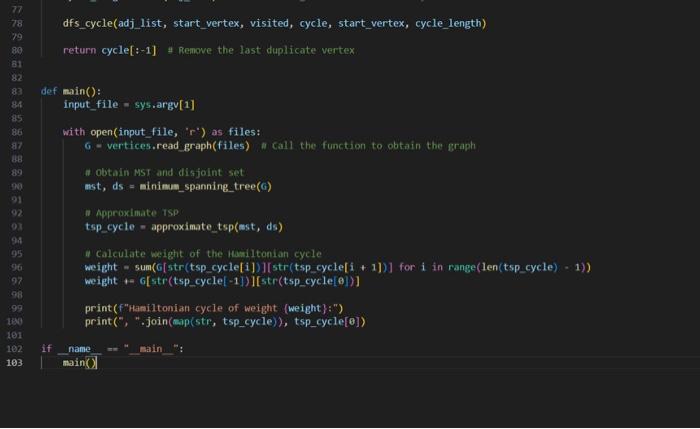
here is the code( i can't attach directly so here are screenshots)
0,1,20,2,70,3,60,4,41,2,61,3,51,4,32,3,22,4,83,4,7 acsc 349, Assierent 8 + triven codt, rats in + Woret do nat aiferithis file. class wightedoroph: "*- A collection of vertices connected by weighted etges "** def = init_ (self, vertices - [1): - The backine adjacency dictionary: selfinatrix - (vertex: i) for vertex in vertices) def _eq (self, other): return type(other) = thightedsraph and self, matrix - other, matrix def_repr_(self): [z; xs=x(repr(v),repr(self(v])) for v in self ] def_len_(self): return len(self, sitrix) def_iter_(self): return iter(self.eatrix) def_contains_(self, Iten): return ites in seif, sitrix def getites (self, key): return self, matrix[key] def setitem (self, key, value): self, matrix[key] = value And add vertex(graph, vertex): Add a vertex to a eraph. if it does not exist. iparan graph: A graph to which to add a vertex ipara vertex: the vertex to be added sroturn: The vertex's adjacency dictionary sint return sraph.esitrix. setdefault (vertex, (y) def add_edge(Braph, vertex_u, vertex_v, weight): Add an edge to a graph, adding vertices finst if they do not exist. tparae graph: A graph to which to add an edse tparan vertex u: the edge's first endpoint iparan vertexivi the edfe's second endpoint iparan woight: The woight of the edge iretarn: The resultins Broph net add vertex(graph; vertex u ) [vertex_y] - weight add vertex(Braph, vertex. v ) [vertex u] - weight return graph def renove vertex(Braph, vertex): henove a vertex from a graph If it exists, along with all incident edges. tparan graph: A graph froe which to remove a wetex tparan vertex: The vertex to be remaved tretsirn: the vertox's former idjucency set foc neighbor in graph,matrix-get (vertex, (J): graph-matrix-get(neighbor, { ) . pop (vertex, visig) return graph.matrix+pop(vertex, (1)) def renove edge(graph, vertex u, vertex v) : Aenove an cotec from a graph if it oxists tparan graph: A groph from which to remove an edge iparan vertex u: The edge's first endpolint tparan vertex w : The edge's second endpoint ireturnt the resulting graph eraph.eatrix-get (vertex_y, (b).pop(vertex_ v, thand) graph-matrix.Bet (vertex_y, (0) , pop (vertex_u, nong) return Braph def read_graph(graph_file): "n=" Read a graph from a file. :param graph_file: An open file containing an edge list :return: The corresponding new graph nan graph = WeightedGraph() for u,v,w in map(lambda e: e.split(","), graph_file): add_edge(graph, u.strip (), v.strip (), int(w)) return graph There are numerous problems in computer science that simply cannot be solved efficiently, assuming 1 that P=NP. Since those problems often have real-world applications, it is worthwhile to consider approximating their solutions, effectively trading some amount of correctness for complexity. Part 1: The Traveling Salesperson Problem The Traveling Salesperson Problem, or "TSP", asks for the Hamiltonian cycle of minimum weight in a complete, weighted graph. It is one of the most famously difficult problems in computer science and graph theory 2. In order to make approximation feasible, we restrict the problem to its metric case: all edge weights must satisfy the triangle inequality. For example: In the above complete, weighted graph, the Hamiltonian cycle of minimum weight is (v0,v1,v3,v2,v4,v0). Part 2: Approximating Metric TSP Once restricted to the metric case, there exists a polynomial time approximation algorithm. Note that removing an edge from a Hamiltonian cycle must yield a spanning tree. An MST thus represents a somewhat similar structure to a solution to TSP - but one that is much easier to find. These observations inform a 2-approximation, as follows: 1. Construct an MST, which can be done greedily and requires linearithmic time. In the graph above, there is only one such tree, containing the edges {(v0,v1),(v2,v3),(v1,v4),(v1,v3)}: 1 And it certainly appears to be a safe assumption. 2 Not only is TSP itself NP-Hard, but meroly approximating the getueral case of TSP is also NP-Hard. You now have two approaches for solving this problem: one that sometines works in logarithmic time, and one that aluays works in linear time. Recall that when two functions are added together, the larger eventually dominates the sum: O(logn)+O(n)=O(n). That is to say, there is no asymptotic petalty to simply trying the logarithmic algorithm first 1. Put another way, the linear algorithm was going to recurse on all subproblems regardless, so there is no penalty to using the logarithmie algorithm's approach in deciding which subproblem to recurse on first. If the logarithmic algorithm can find the missing element, you have solved the problem in O(logn) time. If it cannot, you can fall buck on the linear algorithm, thereby solving the problem in a combined O(n) time. In your programming language of choice (see Assignment 1), implement a divide and conquer algorithm to find the missing element of a given sequence: - Your implementation must first attempt to solve the problem in binary-search-based logarithmic time. - Your implementation must resort to merge-sort-based linear time if and only if that first attempt fails. In order to incorporate the linear approach, your implementation will likely deviate from your logarithmic pseudocode designed in Part 2. You may assume that all sequences will contain multiple comma-separated integers, sorted in ascending order, such that exactly one of the possible integers does not exist as an element. For example, the second of the above sequences would be represented as: 2,1,0,1,3,4,5,6,7,8,9 Your program must accept as a command line argument the name of a file containing a sequence as described above, then print to stdout the missing element. For example: >$./compile.sh>$./run.shin1.txt2 Your program will be tested using diff, so its printed output must match cxactly. assgndpy 3 inport sys import weighted grapti as vertices class oisjointset: dof init (self, vertices): self.parent = (vertex: vertex for vertex in vertices } self, rank = \{vertex: for vertex in vertices \} def find(self, vertex): if self, parent[vertex] I= vertex: self, parent [vertex] = self, find(self, parent [vertex]) return self. parent[vertex] def union(self, u,v) : root u=self, find (u) root v=self, find (v) if rootl i= root v : if self, rank[rootu] > self.rank[root v] : self.parent [root_v] = root_u else: self.parent [root u]=rootv if self,rank[root u] wne self,rank[root v ]: self, rank [root v]+=1 def nininum_spanning tree(G): vertices - list(6) a get vertices from the proph using fteration edges =[] for a in 6 : for v, weight in G[u]+iten() : edges.append ( u,v, woight )) inst =[1] ds =0 isjointsot(vertices) for edge in edges: u,v, weight = edge if ds.find (u) I=ds.find(v): ds union (u,v) mat.append( (u,v, woight)) return mst, ds def dfs_cycle(adj_list, start, visited, cycle, start_vertex, cycle_length): print(f"visiting vertex: { start \}") visited[start] = True cycle.append(start) print(f"cycle: (cycle)") if len(cycle) = cycle_length and set(visited.values ())= (True) : print( "Hamiltonian cycle found: \{cycle\}") return for neighbor in adj_list[start]: if not visited[neighbor]: dfs_cycle(adj_list, neighbor, visited, cycle, start_vertex, cycle_length) if len(cycle) > cycle length: cycle.pop() def approximate_tsp(mst, ds): adj_list = (vertex: [] for vertex in ds.parent) for u,v, _ in mst: adj_1ist [u]. append (v) adj_1ist[v].append (u) start_vertex =1 ist (ds, parent.keys ()) [0] visited = \{vertex: False for vertex in ds,parent } cycle =[] cycle_length = len(adj_list) +1 \# The length of a Haniltonian cycle dfs_cycle(adj_list, start_vertex, visited, cycle, start vertex, cycle length) return cycle[:-1] \# Renove the last duplicate vertex dfs_cycle(adj_list, start_vertex, visited, cycle, start_vertex, cycle_length) return cycle[:-1] \& Renove the last duplicate vertex def min() : input file = sys.argu[1] with open(input file, ' r ') as files: G - vertices.read graph(files) a call the function to obtain the graph in obtain MsT and disfoint set mst, ds = - einimun_spanning_tree(G) in Aproximate isp tsp_cycle = approximate_tsp(est, ds) " calculate weight of the maciltonion cyele weight =sum(G[str(tsp_cycle[i])][str(tspcycle[i+1])] for i in range(1len(tspcycle)1)) weight +=G[str(tspcycle[1])][str(tspcycle[])] print(f"Haniltonian cycle of weight (weight):") print(", ".join(eap(str, tsp_cycle)), tsp_cycle[0]) if name = main ": main()