Answered step by step
Verified Expert Solution
Question
1 Approved Answer
this is not a math project, it's a java project (coding) please help. Project 3: Fun with Curve Math 1 Objective This project will require
this is not a math project, it's a java project
Project 3: Fun with Curve Math 1 Objective This project will require indefinite loops to do its work. You will also get a chance to display information to, and gather input from, the user. The project's subject matter ties in nicely with the math that you have studied. It will also test your ability to design your approach, develop incrementally, and test. 2 Background We are working with a parabola specified by this equation: f(x) = -(x2) + 25 with X's domain in the range 0 to 5 (inclusive). The partial parabola looks like this: Parabola: f(x) = -(x2)+25 30 25 20 15 10 5 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.5 2.75 3 3.25 3.5 3.75 4 4.25 4.5 4.755 For example, when the x coordinate is 4, the y coordinate is -(42) + 25 = -16+ 25 = 9 The slope of the line at a given point is given by: f'(x) = -2x (determined using limits or calculus), so for example when the x coordinate is 2.5, the slope of the line is 2.2.5 = -5. 3 Area Estimation The area under the curve can be estimated by using a series of rectangles, each of which starts at a calculated value of x, with a width specified by 5 (X's maximum domain divided by how many rectangles we are using) and the rectangle's left-side y determined by the parabola's defining equation. This is called a Left Riemann Sum. Note the number of rectangles might be greater than the x domain, e.... 15 when x the graph crosses the x axis at 5 as shown below. Were we to visualize the estimation for five rectangles, it would look like this: Parabola: f(x) = -(x2)+25 30 25 20 Area (0) "5 -(0)25)91 - 10.25) 25 Area (1) 5 61%)-25)"} 0-1 -25)*1- 24 15 Area (235/ 6-12-25)'1- (4-25)*1 21 10 Are 123) She H3)-251 (-9.25)*1- 16 5 14 0 E 3.25 SE 3.75 4.25 The total area is the sum of the areas of all the rectangles, in this case 25 + 24 + 21 + 16 + 9 = 95. The more rectangles one uses, the closer the resulting estimation to the actual area. Note that in this example there are a lot of integers; that will not always be the case, e.g., for n>r. Be careful with this. The actual area as determined by limits or calculus is: (125 - 13) = 83.33. So, after we calculate the area using rectangles, we can tell how far off the estimate is. In this case it's 14% too big the overestimation is apparent from the graph, in fact. 4 User Interface Display this menu: Parabola calculations Menu 1. Find y for a given x 2. Find the slope of the tangent line at a given x 3. Calculate area estimate 4. Exit the program Enter your choice: Keep the user within the menu system until they choose to exit, i.e., they can do more than activity while they are there. If the user enters an integer outside the range of valid menu choices or an invalid data type, tell them they have made an error. More details about the menu choices: 1. Ask the user for an x coordinate, then report to them the corresponding y value. 2. Ask the user for an x coordinate, then report to them the slope of the tangent line. 3. Ask the user how many rectangles to use, then report to them the calculated area and how far off the calculation is from the actual. 4. Exits gracefully (not artificially) from the program (i.e., a loop should end, you should not forcibly terminate the program or break out of the loop). 4.1 Gathering User Input Use a Scanner object to get keyboard input from the user. 5 Code Implementation Create two separate classes, one that deals with the user, and one that does the math computations Examples of this type of code division can be found in My Math.java and TestMyMath.java. Follow the Course Style Guide. 5.1 ParabolaCalc Class This class should have no user communication; it is purely a supplier of calculation functions. There should be no main method here. Write static methods for calculations that accept parameters and return results. Provide three public methods, one for each of the specified calculations. Helper functions may be created. Functions must implement precondition tests on parameter values and throw exceptions when appropriate (see section 4.4 in your text). 5.2 Parabola App Class This "main" class should contain all user communication, consisting of console display and user input via the Scanner class. This class is a client of calculation functions from the ParabolaCalc class. This class should have a main method. You may define class constants, but no other class-level variables. Implement generic (not problem-specific) functions to get in-range integers and floating-point values from the user. Pass in the expected minimum and maximum; the functions should ensure the user makes an entry in the specified range and using the right data type (using Scanner look-ahead) and then passes back the user's choice. You'll make of use of such functions in later projects. Create only one Scanner object instance. If you don't understand why, think and ask! It's a common misconception that more are needed. 5.3 General Use procedural decomposition. Further decomposition is allowed if you think it helpful (coding) please help. 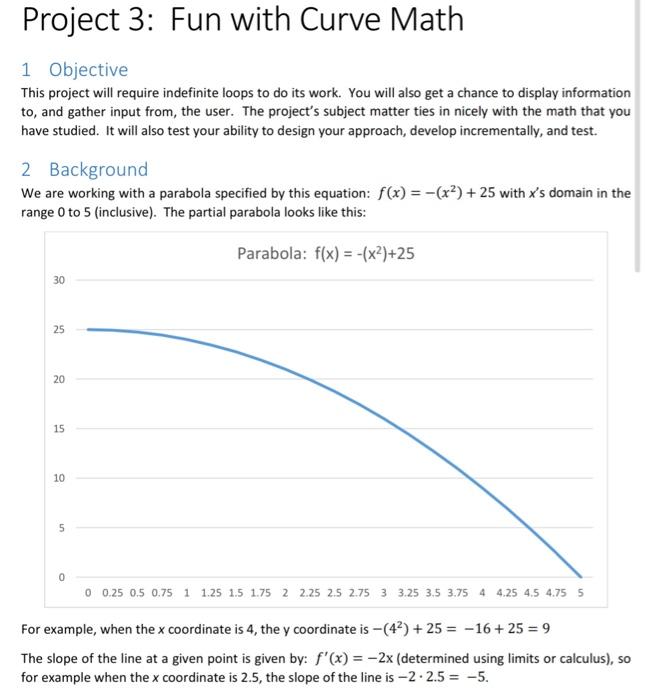





Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


