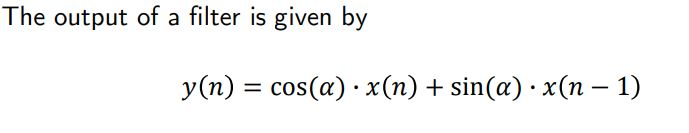
This is part B), don't mind the part C.

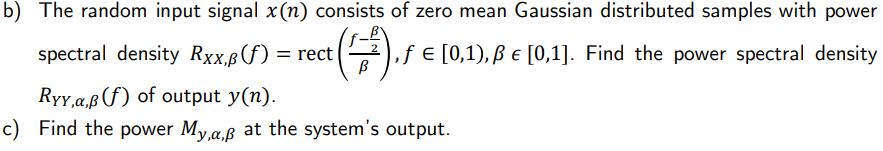
Can You please solve this task? It's really important. Thanks in advance!

The output of a filter is given by y(n) = cos(a) x(n) + sin(a) x(n - 1) e) In real applications, you have mostly access to independent, zero mean, unit-variance Gaussian distributed samples w(n). How can you built (from w(n)) samples x(n) with power spectral density as in point b)? Verify on Matlab. b) The random input signal x(n) consists of zero mean Gaussian distributed samples with power spectral density Rxx, (f) = rect ,fe [0,1), [0,1]. Find the power spectral density Ryy,a, (f) of output y(n). c) Find the power My,a, at the system's output. B The output of a filter is given by y(n) = cos(a) x(n) + sin(a) x(n - 1) e) In real applications, you have mostly access to independent, zero mean, unit-variance Gaussian distributed samples w(n). How can you built (from w(n)) samples x(n) with power spectral density as in point b)? Verify on Matlab. b) The random input signal x(n) consists of zero mean Gaussian distributed samples with power spectral density Rxx, (f) = rect ,fe [0,1), [0,1]. Find the power spectral density Ryy,a, (f) of output y(n). c) Find the power My,a, at the system's output. B