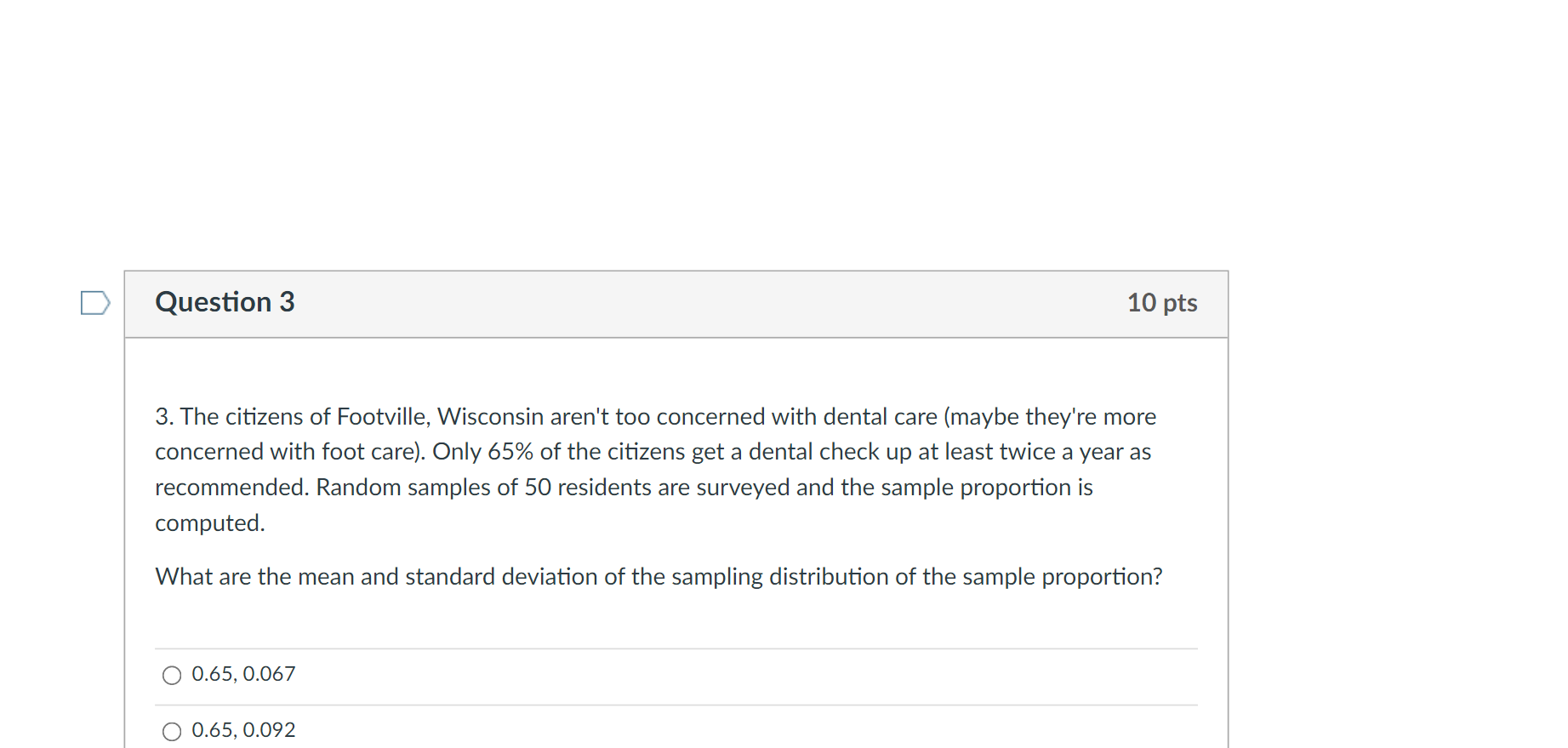
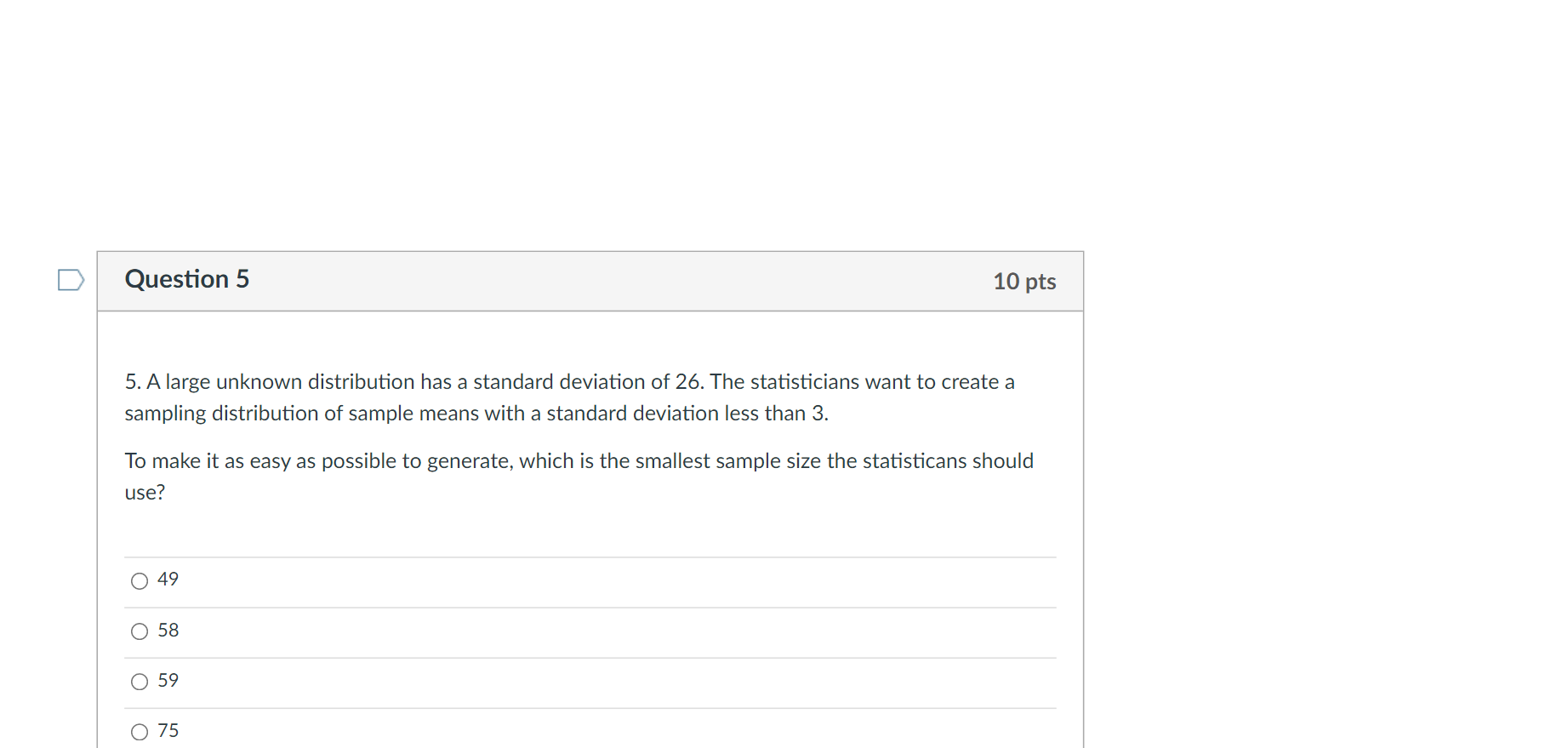
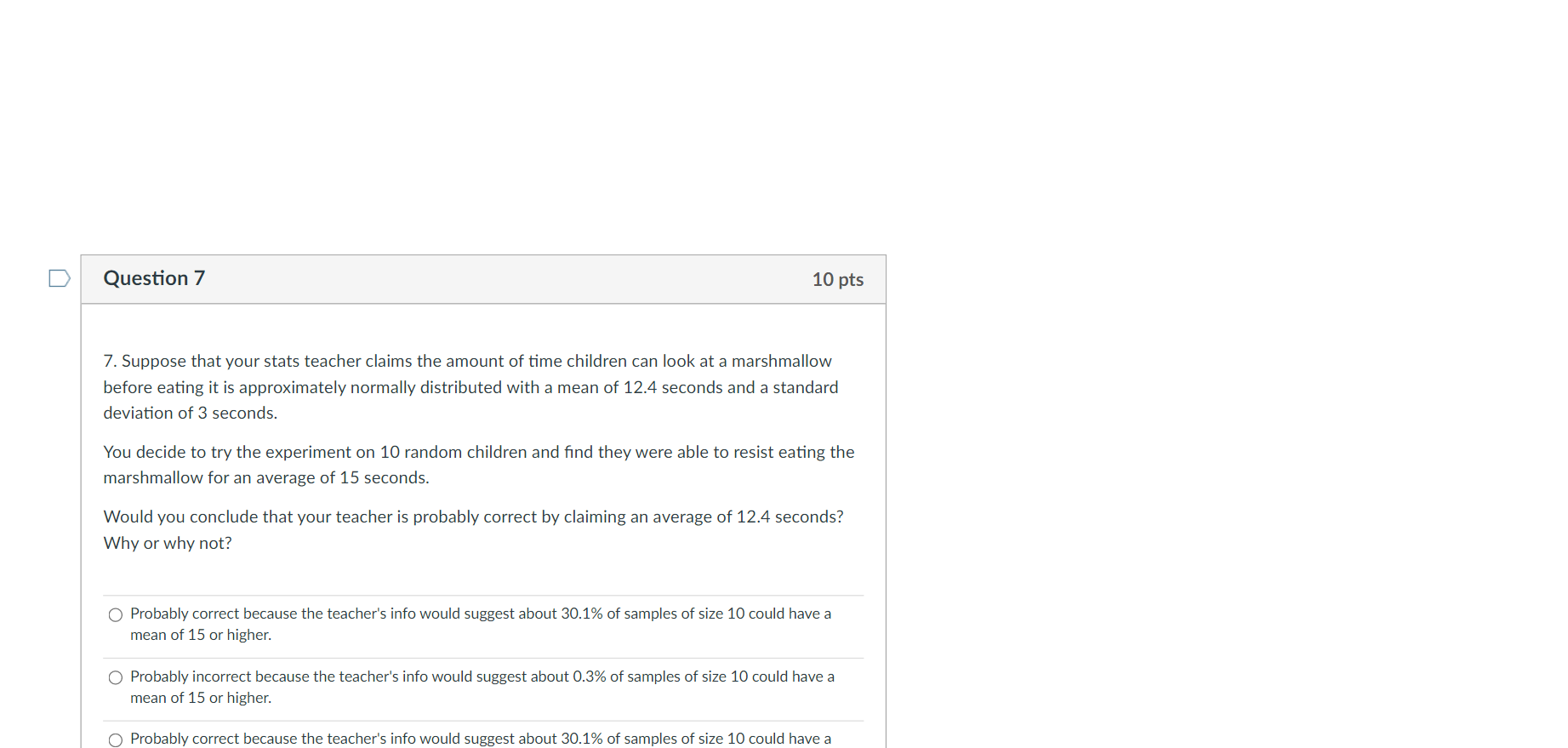
This is statistics course and sampling and Central Limit lesson

I need help with those questions. Thank you.

And I attached formula sheet in case you need it for the references.

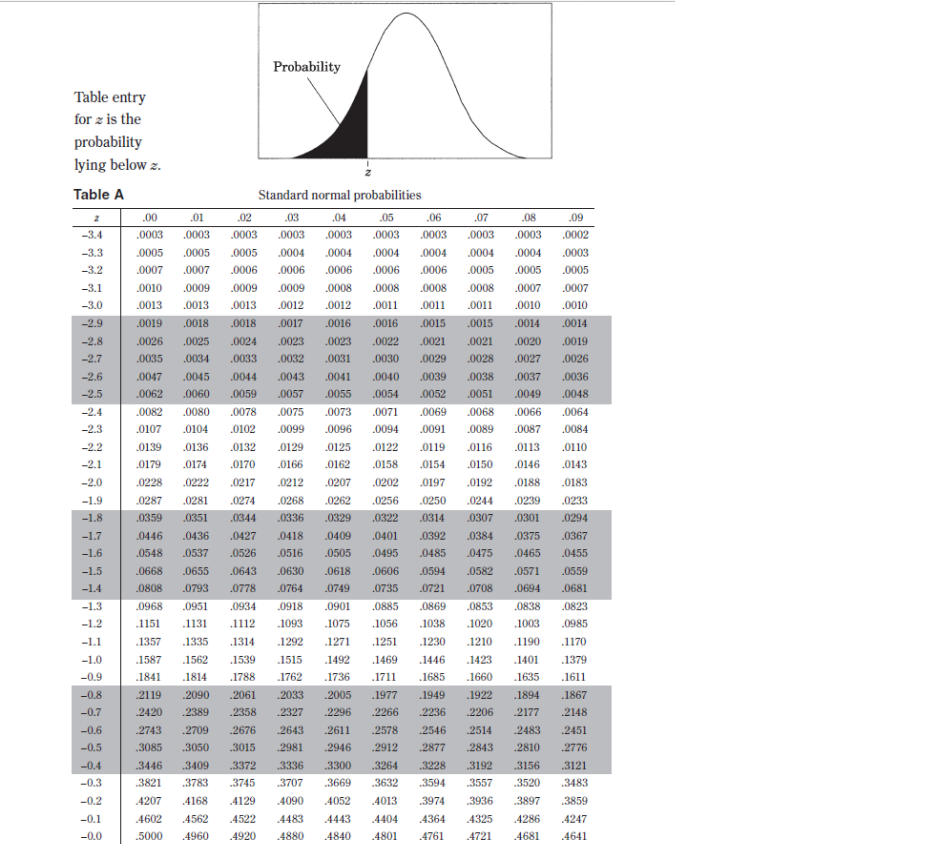
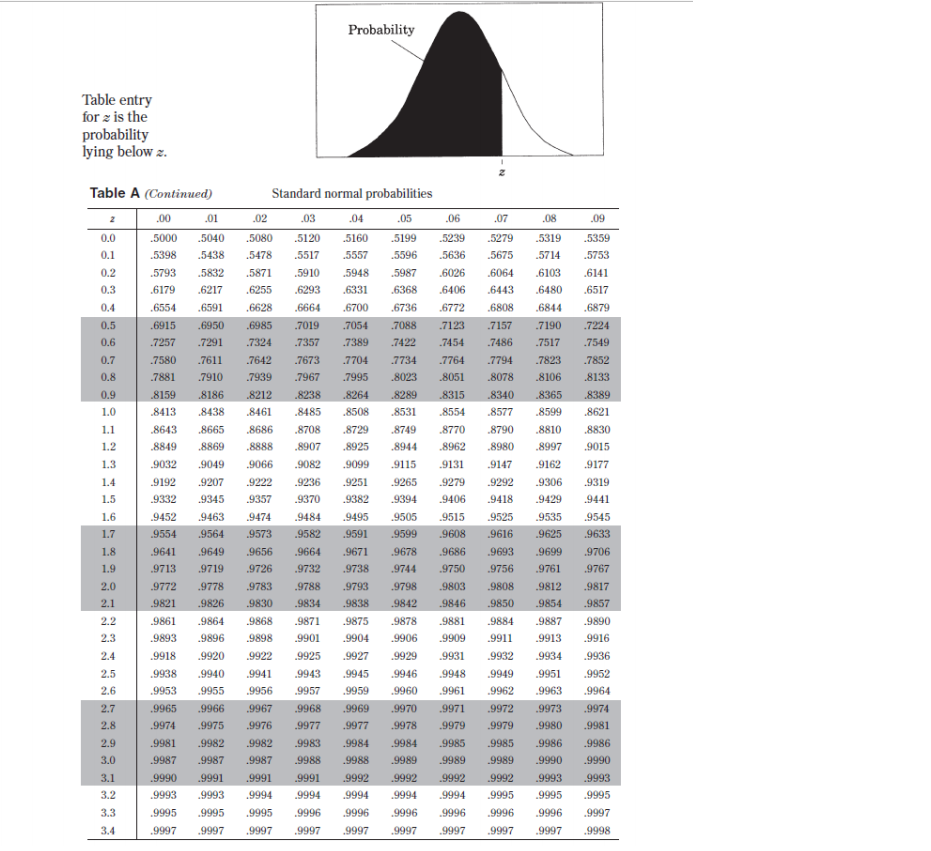
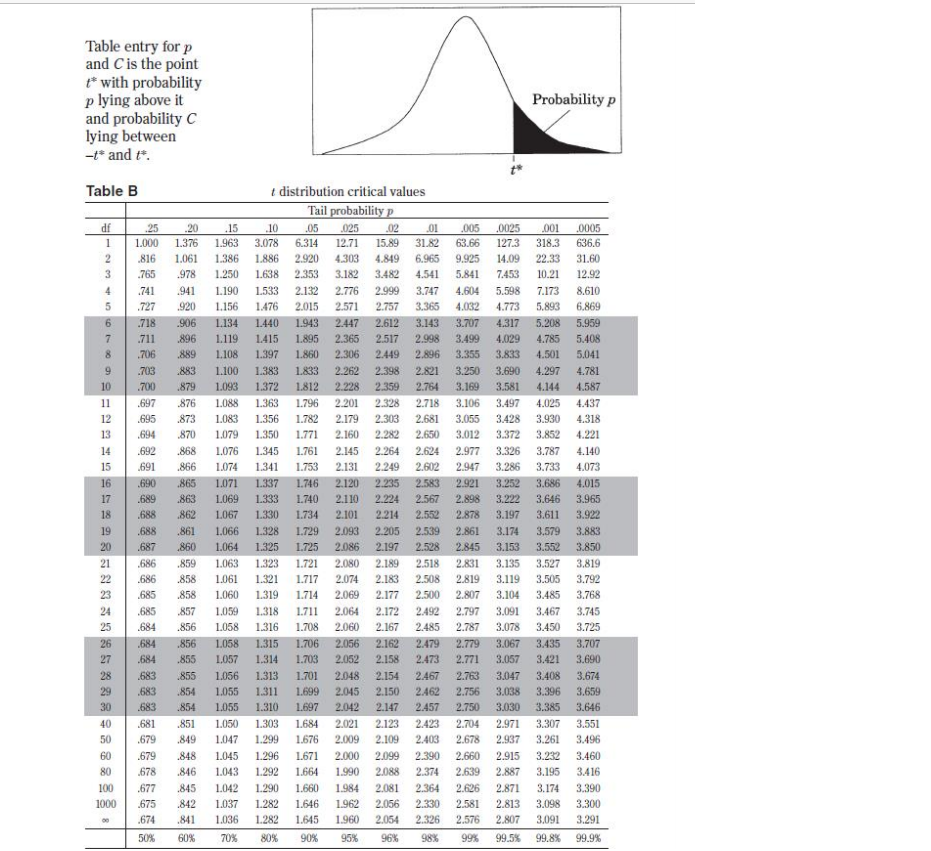
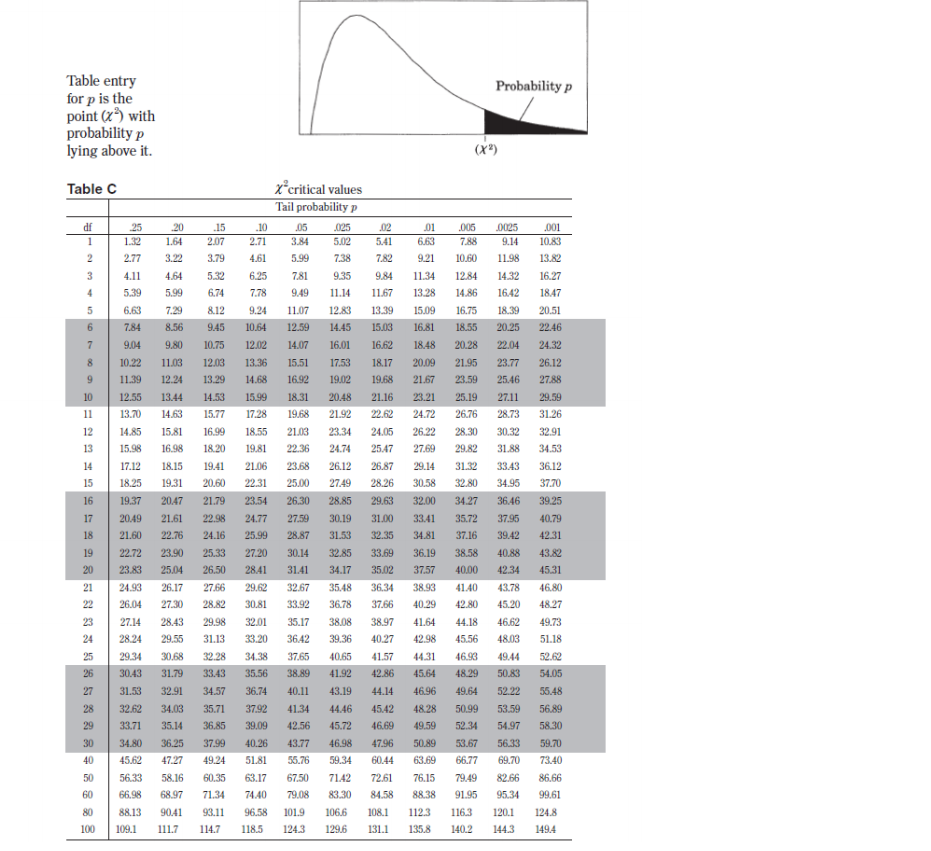
\fII. Probability P(AUB) = P(A) + P(B) - P(An B) P(AB) = P(An B) P(B) E(X) = Ur = _xiPi Var(X) = 03 = _(x1 - Ux)2 Pi If X has a binomial distribution with parameters n and p, then: P(X = k) = k)p* (1 - p)"-k Hx = np Ox = Vnp(1- p) Hi = P Op = P(1 - p) n If r is the mean of a random sample of size n from an infinite population with mean u and standard deviation o, then: HI = H OF = VnIII. Inferential Statistics Standardized test statistic: statistic - parameter standard deviation of statistic Confidence interval: statistic + (critical value) . (standard deviation of statistic) Single-Sample Statistic Standard Deviation of Statistic Sample Mean Sample Proportion p(1 - p) n Two-Sample Statistic Standard Deviation of Statistic Difference of sample means n2 Special case when 0 =02 Difference of P (1 - PI) + P2 (1 - P2) sample proportions n2 Special case when P = P2Probability Table entry for z is the probability lying below z. Table A Standard normal probabilities .00 .01 .02 .03 -05 .06 07 -08 .09 -3.4 0003 .0003 .0003 0003 0003 .0003 0003 .0003 .0003 .0002 -3.3 .0005 .0005 .0005 0004 .0004 .0004 .0004 0004 0004 .0003 -3.2 .0007 0007 0006 .0006 20006 .0006 0006 .0005 .0005 0005 -3.1 0010 0009 0009 0009 0008 .0008 0008 0008 0007 0007 -3.0 .0013 .0013 -0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 -2.9 .0019 .0018 .0018 .0017 .0016 .0016 0015 .0015 .0014 .0014 -2.8 .0026 .0025 0024 .0023 0023 .0022 .0021 0021 .0020 .0019 -2.7 .0035 .0034 0033 .0032 .0031 .0030 0029 0028 0027 0026 -2.6 0047 .0045 .0044 .0043 .0041 .0040 .0039 0038 0037 .0036 -2.5 .0062 .0060 .0059 .0057 .0055 .0054 .0052 .0051 .0049 .0048 -2.4 .0082 0080 .0078 .0075 0073 .0071 .0069 0068 -0066 .0064 -2.3 .0107 .0104 .0102 0099 .0096 .0094 0091 .0089 -0087 0084 -2.2 .0139 .0136 .0132 .0129 .0125 0122 .0119 0116 .0113 .0110 -2.1 .0179 .0174 .0170 .0166 .0162 .0158 0154 0150 .0146 0143 -2.0 .0228 .0222 .0217 0212 .0207 .0202 0197 .0192 .0188 0183 -1.9 .0287 .0281 .0274 0268 .0262 .0256 0250 0244 0239 .0233 -1.8 .0359 .0351 .0344 .0336 .0329 .0322 .0314 .0307 ,0301 .0294 -1.7 .0446 .0436 .0427 0418 0409 .0401 0392 .0384 10375 0367 -1.6 .0548 .0537 .0526 0516 -0505 .0495 0485 .0475 .0465 0455 -1.5 .0668 -0655 .0643 0630 _0618 .0606 0594 .0582 .0571 .0559 -1.4 .0808 .0793 0778 .0764 .0749 0735 0721 .0708 10694 0681 -1.3 .0968 .0951 .0934 0918 -0901 .0885 0869 .0853 .0838 0823 -1.2 .1151 .1131 .1112 1093 .1075 1056 1038 .1020 1003 0985 -1.1 .1357 .1335 .1314 .1292 .1271 .1251 1230 .1210 .1190 .1170 -1.0 .1587 1562 .1539 .1515 .1492 .1469 1446 .1423 .1401 .1379 -0.9 .1841 .1814 .1788 1762 .1736 .1711 1685 .1660 .1635 .1611 -0.8 .2119 .2090 2061 2033 .2005 .1977 1949 1922 .1894 .1867 -0.7 .2420 2389 2358 2327 2296 .2266 2236 .2206 .2177 .2148 -0.6 .2743 .2709 .2676 .2643 2611 12578 .2546 .2514 .2483 2451 -0.5 .3085 .3050 3015 2981 2946 2912 .2877 .2843 .2810 .2776 -0.4 .3446 .3409 .3372 .3336 3300 .3264 3228 3192 .3156 .3121 -0.3 .3821 .3783 .3745 .3707 3669 3632 .3594 3557 .3520 3483 -0.2 4207 4168 4129 4090 .4052 4013 3974 3936 3897 .3859 -0.1 4602 4562 4522 4483 4443 .4404 4364 -4325 4286 .4247 -0.0 .5000 .4960 .4920 4880 .4840 .4801 4761 4721 .4681 .4641Probability Table entry for > is the probability lying below z. Table A (Continued) Standard normal probabilities 2 .00 01 .02 .03 .04 .05 .06 .07 .08 -09 0.0 5000 5040 .5080 5120 5160 .5199 5239 5279 -5319 .5359 0.1 5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 -5714 .5753 0.2 .5793 .5832 .5871 .5910 5948 .5987 6026 .6064 .6103 .6141 0.3 6179 6217 6255 6293 6331 6368 6406 6445 .6480 6517 0.4 6554 6591 6628 6664 6700 6736 6772 6808 6844 6879 0.5 .6915 .6950 6985 .7019 .7054 .7088 .7123 7157 .7190 7224 0.6 7257 7291 7324 7357 7389 .7422 .7454 7486 .7517 .7549 0.7 7580 7611 7642 7673 7704 7734 .7764 7794 7823 17852 0.8 7881 7910 7935 7967 7995 8023 .8051 8078 .8106 .8133 .8159 8186 8212 8238 8264 .8289 8315 8340 8365 .8389 0.9 8461 8485 8508 .8531 .8554 8577 8594 8621 1.0 8413 8438 .8643 8665 8708 8729 8749 8790 8810 1.1 .8770 8830 8686 1.2 8849 8869 8888 690M 8925 .8914 8962 8980 8997 .9015 1.3 9032 9049 9066 9082 9099 .9115 .9131 9147 9162 9177 1.4 9192 9207 9222 9236 .9251 9265 .9279 9292 9306 .9319 1.5 9332 9345 .9357 9370 9382 9394 9406 9418 .9429 .9441 1.6 9452 .9463 .9474 9484 9495 9505 9515 9525 9535 .9545 9554 9564 9573 9582 9591 9599 9608 9616 9625 9633 1.7 9649 9656 9664 .9678 9686 9693 9706 1.8 9641 ,9671 9699 9761 .9767 1.9 9713 .9719 9726 9732 9738 .9714 9750 9756 9812 .9817 20 9772 .977 9783 9788 9793 9798 9803 9808 2.1 9821 19826 9830 9834 9838 9842 9846 9850 .9854 .9857 2.2 9861 .9864 9868 9871 .9875 .9878 9881 9884 .9887 9890 .9896 9901 .9904 9906 .9909 9911 9913 .9916 2.3 .9893 9898 2.4 9918 9920 9922 9925 9927 992 9931 9932 .9934 9936 9938 .9940 9941 9943 .9945 9946 9948 .9949 .9951 .9952 2.5 9953 9959 .9961 9964 9955 995 9957 .9960 9962 .9963 2.6 2.7 .9965 .9966 9967 .9968 .9969 .997 9971 9972 9973 .9974 2.8 .9974 .9975 9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981 .9981 .9982 .9982 9983 19984 .9984 9985 9985 .9986 .9986 2.9 3.0 9987 .9987 4987 9988 9988 9989 9989 9989 9990 .9990 3.1 .9990 .9991 9991 9991 9992 9992 9992 9992 9993 .9993 3.2 .9993 .9993 .9994 9994 .9994 .9994 .9994 .999 .9995 .9995 3.3 .9995 .9995 .9995 9996 9996 .9996 .9996 .9996 9996 .9997 3.4 9997 9997 9997 .9997 9997 9997 .9998 .9997 .9997 .9997Table entry for p and C is the point #* with probability p lying above it Probability p and probability C lying between -t* and * Table B t distribution critical values Tail probability p df .25 .20 -15 10 05 .025 .02 .01 .005 0025 .001 .0005 1.000 1.376 1.963 3.078 6.314 12.71 15.89 31.82 63.66 127.3 318.3 636.6 .816 1.061 1 386 1.886 2.920 4.303 4.849 6.965 9.925 14.09 22.33 31.60 765 .978 1.250 1.638 2.353 3.182 3.482 4.541 5.841 7.453 10.21 12.92 .741 941 1.190 1.533 2.132 2.776 2.999 3.747 4.604 5.598 7.173 8.610 .727 920 1.156 1.476 2.015 2.571 2.757 3.365 4.032 4.773 5.893 6.869 718 906 1.134 1.440 1.943 2.447 2.612 3.143 3.707 4.317 5.208 5.959 .711 896 1.119 1.415 1.895 2.365 2.517 2.948 3.499 4.029 4.785 5.408 .706 1.108 1.397 1.860 2.306 2.449 2.896 3.355 3.833 4.501 5.041 703 883 1.100 1.383 1.833 2.262 2.398 2.821 3.250 3.690 4.297 4.781 10 .700 879 1.093 1.372 1.812 2.228 2.359 2.764 3.169 3.581 4.144 4.587 11 697 876 1.088 1.363 1.796 2.201 2.328 2.718 3.106 3.497 4.025 4.437 873 1.083 1.356 1.782 2.179 2.303 2.681 3.055 3.428 3.930 4.318 1.079 1.350 1.771 2.160 2.282 2.650 3.012 3.372 3.852 4.221 .692 1.076 1.345 1.761 2.145 2.264 2.624 2.977 3.326 3.787 4.140 15 691 1.341 1.753 2.131 2.249 2.612 2.947 3.286 3.733 4.073 16 69 865 1.071 1.337 1.746 2.120 2.235 2.583 2.921 3.252 3.686 4.015 17 .685 LU69 1.333 2.110 2.224 2.567 2.898 3.222 3.646 3.965 18 1067 1.330 1.734 2.101 2.214 2.552 2.878 3.197 3.611 3.922 19 .688 861 1.066 1.328 1.729 2.093 2.205 2.539 2.861 3.174 3.579 3.883 20 687 $60 1.064 1.325 1.725 2.086 2.197 2.528 2.845 3.153 3.552 3.850 21 .686 859 1.063 1.323 1.721 2.080 2.189 2.518 2.831 3.527 3.819 22 .686 858 1.061 1.321 1.717 2.074 2.183 2.508 2.819 3.119 3.505 3.792 23 685 858 1.060 1.319 1.714 2.069 2.177 2.500 2.807 3.104 3.485 3.768 24 .685 857 1.059 1.318 1.711 2.064 2.172 2.492 2.797 3.467 3.745 25 684 356 1058 1.316 1.708 2.060 2.167 2.485 2.787 3.078 3.450 3.725 26 684 856 1058 1.315 1.706 2.056 2.162 2.479 2.779 3.067 3.435 3.707 27 .684 855 1.314 1.703 2.052 2.158 2.473 2.771 3.057 3.421 3.690 28 683 855 1.056 1.313 1.701 2048 2.154 2.467 2.763 3.047 3.408 3.674 29 68 854 1,055 1.311 1.699 2.045 2.150 2.462 2.756 3.038 3.396 3.659 30 .683 854 1.055 1.310 1.697 2.042 2.147 2.457 2.750 3.030 3.385 3.646 40 .681 851 1.050 1.303 1.684 2.123 2.423 2.704 3.307 3.551 50 679 849 1.047 1.299 1.676 2.009 2.109 2.403 2.678 2.937 3.261 3.496 60 679 .848 1.045 1.296 1.671 2.000 2.099 2.390 2.660 2.915 3.232 3.460 80 678 846 1043 1.292 1.664 1.990 2088 2.374 2.639 2.887 3,195 3.416 100 .677 .845 1.042 1.290 1.660 1.984 2.081 2.364 2.626 2.871 3.174 3.390 1000 .675 842 1.037 1.282 1.646 1.962 2.056 2.330 2.581 2.813 3.098 3.300 674 841 1.036 1.282 1.645 1.960 2.054 2.326 2.576 2.807 3,091 3.291 50% 60% 70% 80% 90% 95% 96% 98% 99% 99.5% 99.8% 99.9%%Table entry Probability p for p is the point (x ) with probability p (X ?) lying above it. Table C x critical values Tail probability p .02 01 0025 dif 25 20 .15 -10 .05 1025 005 .001 2.71 3.8 5.02 5.41 6.63 7.8 9.14 10.83 1.32 1.64 2.07 3.79 4.61 5.99 7.38 7.82 921 10.60 1198 13.82 2.77 3.22 6.25 781 9.35 984 11.34 12 84 14 32 16.27 4.11 4.64 5.32 5.39 5.90 6,74 7.78 9.19 11.14 11.67 13 28 14.86 1642 18.47 15.09 18 39 20.51 6.63 8.12 9.24 11.07 12 89 16.75 40.25 22.46 7.84 8.56 9.45 10.64 12.59 14.45 15.03 16.61 18.51 14 07 16.01 16.62 18.48 22.04 24.32 9.04 9.80 10.75 12.02 21.95 23.77 26.12 10.22 11.03 12 03 13.36 15.51 17.53 18.17 20.09 21.67 23.59 25.46 27.88 11.3 13.29 14.68 16.92 19.02 19.68 12.24 23.21 25.19 29.59 12.5 13.44 14.53 18.31 20.48 21.16 27.11 15.99 28.73 31.26 13.70 14.63 15.77 17.28 19.68 21.92 22.62 24.72 26.76 23.34 24.05 26.22 28.30 30.32 32.91 14.85 15.81 16.94 18.55 21.03 22.36 24.74 25.47 27.69 29.82 31.88 34.53 15.98 16.98 18.20 19.81 21.06 23.68 26.12 26.87 29.14 31.32 33.43 36.12 17.12 18.15 19.41 18.25 19.31 20.60 22.31 25.00 27.49 28.26 30.58 32.80 34.95 37.70 20.47 21.79 23.54 26.30 28.85 29.63 32.00 34.27 36.46 39.25 19.37 30.19 31.00 33.41 35.72 37.95 40.79 20.49 21.61 22.98 24.77 27.59 32.35 34.81 37.16 39.42 42.31 21.60 22.76 24.16 25.99 28.87 31.53 22.72 23.90 25.33 27.20 30.14 32.85 33.69 36.19 38.58 40.88 43.82 26.50 28.41 31.41 34.17 35.02 37.57 40.00 12.34 45.31 23.83 25.04 29.62 32.67 35.48 36.34 38.93 41.40 43.78 46.80 24.93 26.17 27.66 26.04 27.30 28.82 30.81 33.92 36.78 37.66 40.29 12 81 45.20 48.27 38 97 41.64 14.18 16 62 49.73 27.14 28.43 29 98 35.17 38.08 39.36 40.27 42.98 45.56 1803 51.18 28 2 2955 31.13 23.20 3642 32.28 14.38 37.65 40.65 41.57 44.31 46.93 29.3 33.43 15.56 38.89 41.92 12 8 45.64 48 2 54.05 26 30.4 31.79 13.15 14.14 46.96 19.6 52.22 55.48 32.91 34.57 36.74 4011 3.1.5 41.34 14.46 45.42 18 28 50.9 53.59 56.89 28 32.6 34.03 35.71 37.92 58.30 16069 19.59 52.3 54.97 33.7 35.14 36.85 39.09 42.56 15.72 34.80 36.25 37.9 40.26 43.77 46.98 47.96 50.89 53.67 56.3 59.70 45.62 47.27 49.24 51.81 55.76 59.34 60.44 63.69 66.77 69.70 73.40 79.49 $2.66 86.66 56.33 58.16 60.35 63.17 67.50 71.42 72.61 76.15 99.61 66.9 68.97 71.34 74.4 79.08 83.30 84.58 8.8.38 91.95 95.34 124.8 80 88.13 90.41 93.11 96.58 101.9 106.6 108.1 112.3 116.3 120.1 140.2 111.7 131.1 149.4 114.7 118.5 129.6 100 124.3 135.8 144.3 109.1Question 3 10 pts 3. The citizens of Footville, Wisconsin aren't too concerned with dental care (maybe they're more concerned with foot care). Only 65% of the citizens get a dental check up at least twice a year as recommended. Random samples of 50 residents are surveyed and the sample proportion is computed. What are the mean and standard deviation of the sampling distribution of the sample proportion? O 0.65, 0.067 O 0.65, 0.092 Question 5 10 pts 5. A large unknown distribution has a standard deviation of 26. The statisticians want to create a sampling distribution of sample means with a standard deviation less than 3. To make it as easy as possible to generate, which is the smallest sample size the statisticans should use? 049 053 059 075 Question 7 10 pts 7. Suppose that your stats teacher claims the amount of time children can look at a marshmallow before eating it is approximately normally distributed with a mean of 12.4 seconds and a standard deviation of 3 seconds. You decide to try the experiment on 10 random children and nd they were able to resist eating the marshmallow for an average of 15 seconds. Would you conclude that your teacher is probably correct by claiming an average of 12.4 seconds? Why or why not? Q Probably correct because the teacher's info would suggest about 30.1% of samples of size 10 could have a mean of 15 or higher. 0 Probably incorrect because the teacher's info would suggest about 0.3% of samples of size 10 could have a mean of 15 or higher. 0 Probably correct because the teacher's info would suggest about 30.1% of samples of size 10 could have a 10. Answer each question in the box below. 3) Identify all possible samples of size n = 2 that can be obtained from rolling a six-sided die. For example, you roll the die twice and get 4 the rst time and 6 the second time, so (4, 6) is one possible sample of size n = 2. b) Find the mean of each sample. For example, the sample described above, (4, 6) has a mean of 5. Then, show that the mean of the sampling distribution of the means is equal to the mean of the population {1,23,45,63}. c) What is the standard deviation of the population? Explain how to nd the standard deviation of the distribution of the sample means based on the standard deviation of the population