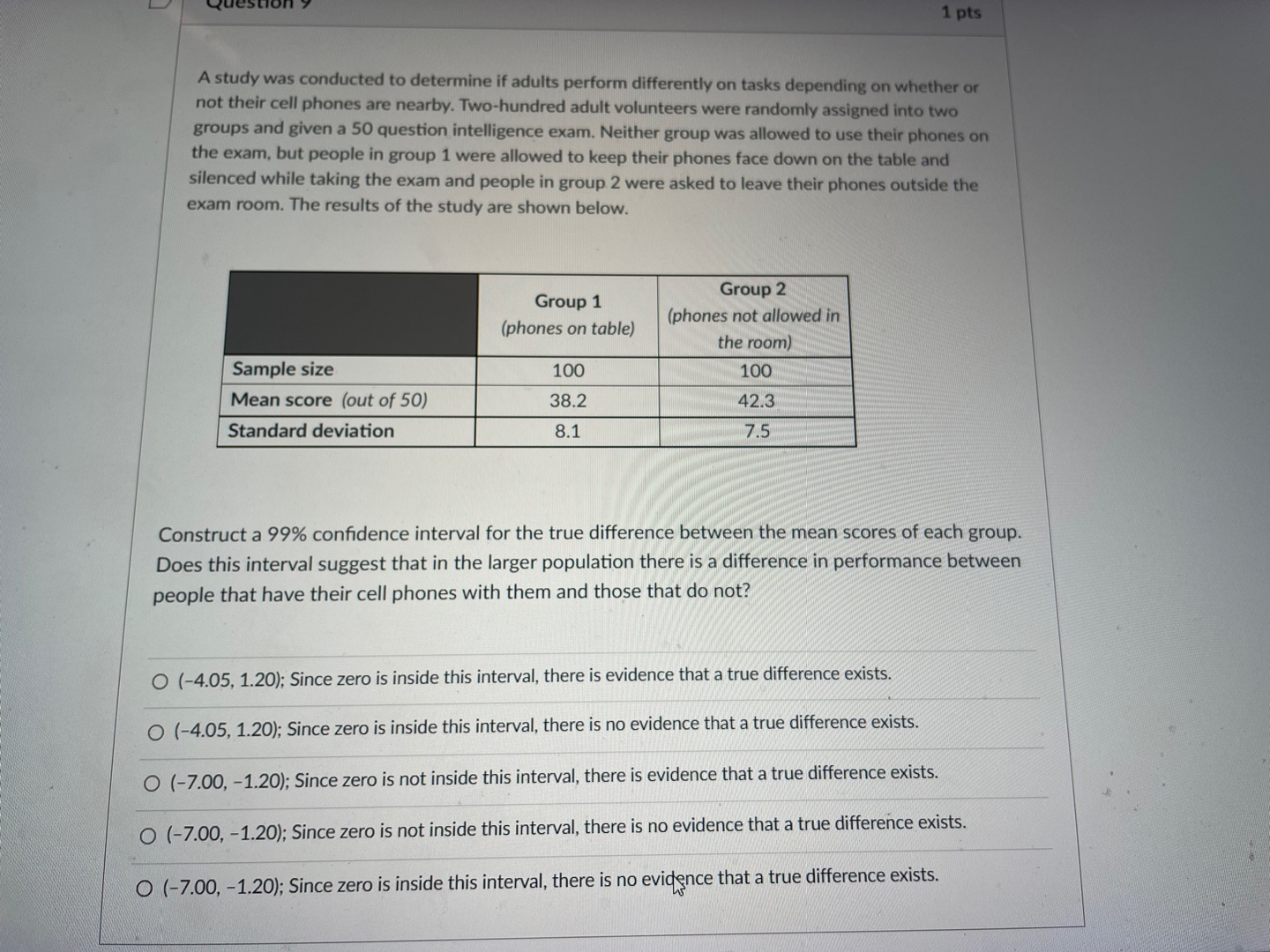
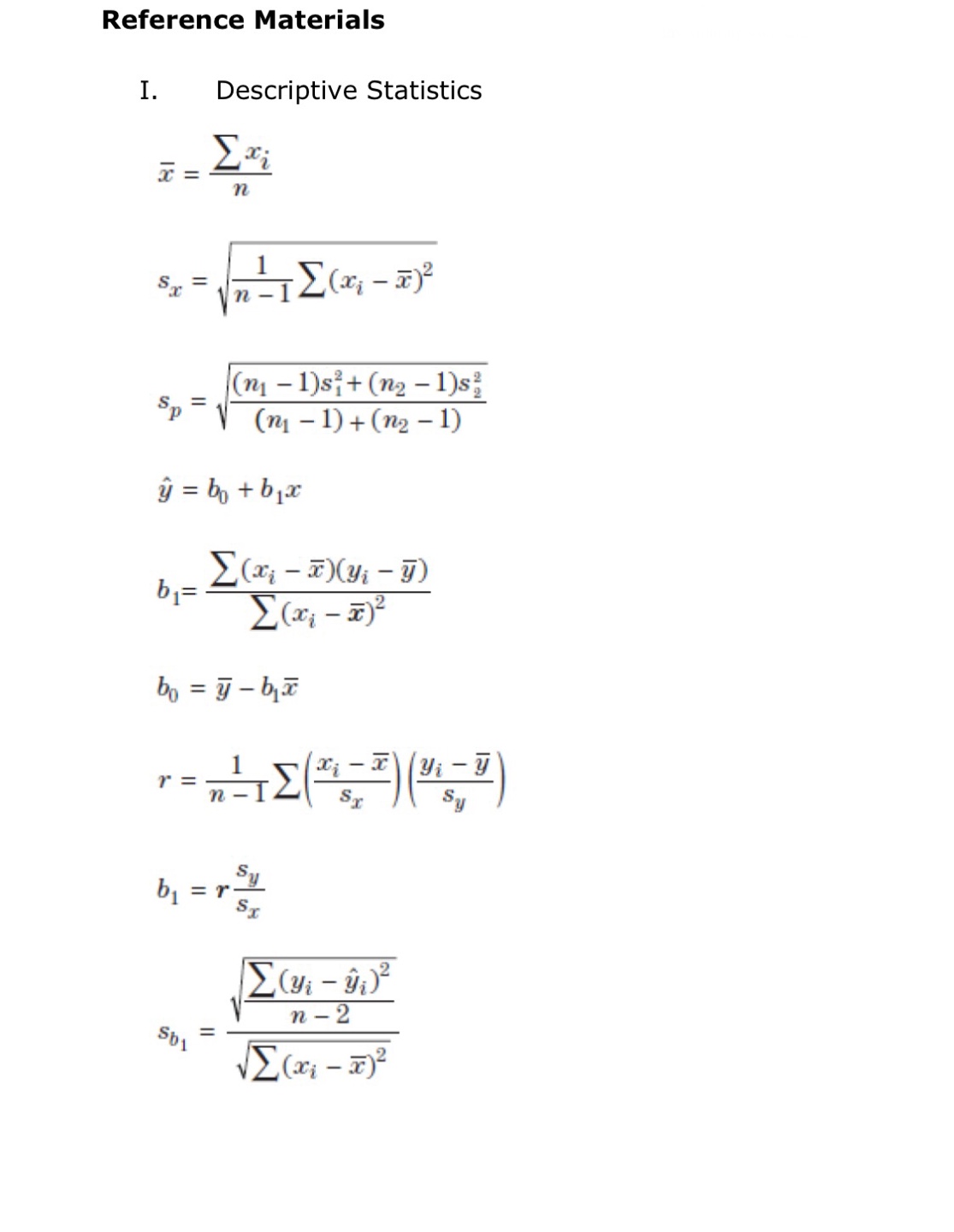This is statistics course, sampling distributions, estimation and tests of significance units.I need help with this. I attached formula sheet in case you need it.

II. Probability P(AUB) = P(A) + P(B) - P(An B) P(AB) = P(An B) P(B) E(X) = Ux = Expi Var(X) = 0; = _(x - ux)2pi If X has a binomial distribution with parameters n and p, then: P(X = k) = k) p* (1 - p)" -* HI = np Or = Vnp(1 - p) Ho = P Op = P(1- p n If x is the mean of a random sample of size n from an infinite population with mean u and standard deviation O, then: MY = HIII. Inferential Statistics Standardized test statistic: statistic - parameter standard deviation of statistic Confidence interval: statistic + (critical value) . (standard deviation of statistic) Single-Sample Statistic Standard Deviation of Statistic Sample Mean Sample Proportion p(1 - p) n Two-Sample Statistic Standard Deviation of Statistic Difference of sample means 722 Special case when 61 =02 ol+1 n2 Difference of PI (1 - PI) + P2 (1 - P2) sample proportions n1 n2 Special case when P1 = P2 Jp(1 - P) 1 + 1 Vn, n2 Chi-square test statistic = \\ (observed - expected) expected1 pts A study was conducted to determine if adults perform differently on tasks depending on whether or not their cell phones are nearby. Two-hundred adult volunteers were randomly assigned into two groups and given a 50 question intelligence exam. Neither group was allowed to use their phones on the exam, but people in group 1 were allowed to keep their phones face down on the table and silenced while taking the exam and people in group 2 were asked to leave their phones outside the exam room. The results of the study are shown below. Group 1 Group 2 (phones on table) (phones not allowed in the room) Sample size 100 100 Mean score (out of 50) 38.2 42.3 Standard deviation 8.1 7.5 Construct a 99% confidence interval for the true difference between the mean scores of each group. Does this interval suggest that in the larger population there is a difference in performance between people that have their cell phones with them and those that do not? O (-4.05, 1.20); Since zero is inside this interval, there is evidence that a true difference exists. O (-4.05, 1.20); Since zero is inside this interval, there is no evidence that a true difference exists. O (-7.00, -1.20); Since zero is not inside this interval, there is evidence that a true difference exists. O (-7.00, -1.20); Since zero is not inside this interval, there is no evidence that a true difference exists. O (-7.00, -1.20); Since zero is inside this interval, there is no evidence that a true difference exists.