THIS IS THE LINK https://phet.colorado.edu/sims/html/masses-and-springs-basics/latest/masses-and-springs-basics_en.html , PLEASE DO THIS ACTIVITY ON A COMPUTER GO TO THE WEBSITE LINK THAT I PUT THE SAME LINK UNDER MATERIALS PLEASE COPY THE LINK ON YOUR COMPUTER TO DO THE EXCERSICES, THANK YOU.

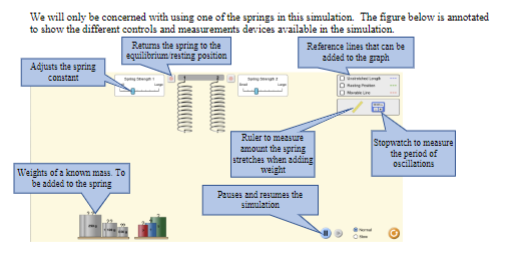
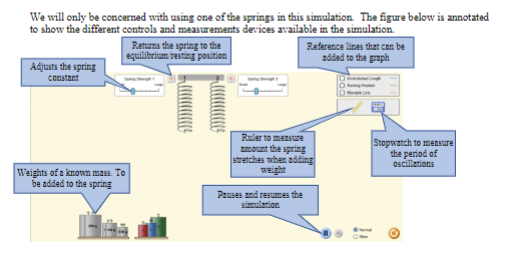
Objective: In this lab exercise we will be discussing measurement accuracy and precision, significant figures, and scientific notation. The notion of measurement accuracy and precision is essential to properly communicating results of a measurement and the final uncertainty in a measurement can be no better than the measurement with the lowest level of accuracy. For example, if you know you are traveling, in a car, at exactly 65 miles per hour for exactly 1 hour. Then you know you traveled exactly 65 miles. However, there is actually uncertainty in the measurement. In practice if you claim you are traveling 65 miles per hour as read on a speedometer with 1 mile per hour resolution then convention states you are traveling 65 1 1 mph. Similarly, if your watch has resolution of only 1 second then you know your travel time is 1 hr 1 1 sec which we can rewrite as 1 0.0003 hrs. This would be the most accurate way to express the uncertainty. But we might just choose to write out that we traveled for 1.000 hrs where we chose to round to 4 significant figures. It should be clear in this case the more significant uncertainty in the determination of how far you actually drove in the hour is the speed at which you are traveling. Therefore, one can not claim a distance traveled better than the uncertainty in the speed. That is to say when you multiply (65 mph x 1.000 hrs = 65 miles) you can't claim you drove 65.000 miles since the uncertainty is dominated by the resolution of the speedometer. In this lab exercise we will first complete a worksheet involving measuring the length of an object using the rulers supplied in this handout. We will then perform an exercise involving accuracy versus precision, followed by a few exercises related to expressing numbers using scientific notation and performing relatively simple calculations concentrating on making sure to express the final answer with the correct significant figures. Finally, you will be running a simulation to determine the spring constant of a spring using several different methods. The formulas to determine the spring constant are given to you in this handout. Your job will be to perform the measurements and also determine which method leads to the most accurate result and why.Materials: This handout, printed . A pencil or pen with length -15 cm (6 inches). Don't worry about being very close to this length, a common pencil or pen is between 14 and 16 cm. Attendance or viewing mini-lecture on significant figures and scientific notation. Computer and Internet access to use the following simulation: https://phet.colorado.edu/sims/html/masses-and-springs-basics/latest/masses-and-springs- basics en.html Investigation A: Resolution of a Ruler Purpose: To understand that the resolution of a measurement device determines how precise of a measurement you can make.Investigation E: Simulation and measurement uncertainty Purpose: To understand and experience measurements of specific values of an object using various techniques and compare the relative precision of these measurements. Introduction: Sometimes you will need to determine specific characteristics of an object by making indirect measurements and then use different physical properties to make a calculation based on quantities you have measured directly. In this simulation we will determine the stiffness of spring or spring constant using Hooke's law as well as using the properties of simple harmonic motion. This handout will give you all the formula's you need to determine the spring constant using the different methods. Your task will be to take the measurements and then calculate the spring constant and then report the value of the spring constant with the appropriate number of significant figures. The simulation we will be using can be found at the following website: https:/phet.colorado.edu/sims/html/masses-and-springs-basics/latest masses-and-springs- basics_en. htmlProcedure: 1) Click on the link above or paste into your browser to open the simulation. Upon Opening you should see the following screen: Masses and Springs: Basics Stretch2) Next click on the box marked Bounce to open the following: OWe will only be concerned with using one of the springs in this simulation. The figure below is annotated to show the different controls and measurements devices available in the simulation. Returns the spring to the Reference lines that can be equilibrium rating position added to the graph Adjusts the spring Foxler to measure Stopwatch to measure amount the spring the period of atreichen when adding oscillations Weights of a known mass. To weight be added to the spring Pamgen and reviamen the O3) Measure the Spring Constant using the displacement method. a) Remove the ruler and position the end and the bottom of spring 1. b) Ensuring the spring strength adjustment is 3 tick marks to the right of the small setting (as shown above) attach the 250g weight to the end of spring 1. c) After the weight is attached the system will start oscillating. Click the stop button to the left of spring 1 to return the spring-mass system to its equilibrium position. Record the position of the bottom of the spring in its" equilibrium but stretched conditions and record the total displacement of the from the spring position before attaching the weight and record in table-1 below (make sure you convert your measurement to meters.). Also, indicate the number of significant figures in your measurement. Mass (kg) Spring Displacement (m) Spring Constant (k) Measured Sig Figs. Calculated Sig Figs. 0.250 0.100 0.050 Hooke's Laws tells us that the force required to stretch a spring a distance x is equal to its stiffness (spring constant) times the displacement from its unstretched length. In this case the Force applied to the spring is mass of the weight times the acceleration due to gravity (g = 9.8 m/s'). Therefore. we can rewrite the above equation to get. my d) Calculate the value for the spring constant and record in table 1 for each of the masses used. Again indicate the number of significant figures in calculated spring constant. e) Repeat Steps 1-6 for the 100g and the 50g masses.4) Next we will measure the spring constant using simple harmonic motion along with the measurement of the period of oscillation and the following formula: T= 2n Where T is the period of oscillation Which we can rewrite as: a) Attach to the 250g mass and click the stop button place the system in the equilibrium position. b) Click the pause button and stretch the spring mass system -20 cm. c) Remove the timer from its holding area and click the play button to start the simulation. d) At either the top or bottom of the oscillation just as the mass is switching direction click the start button