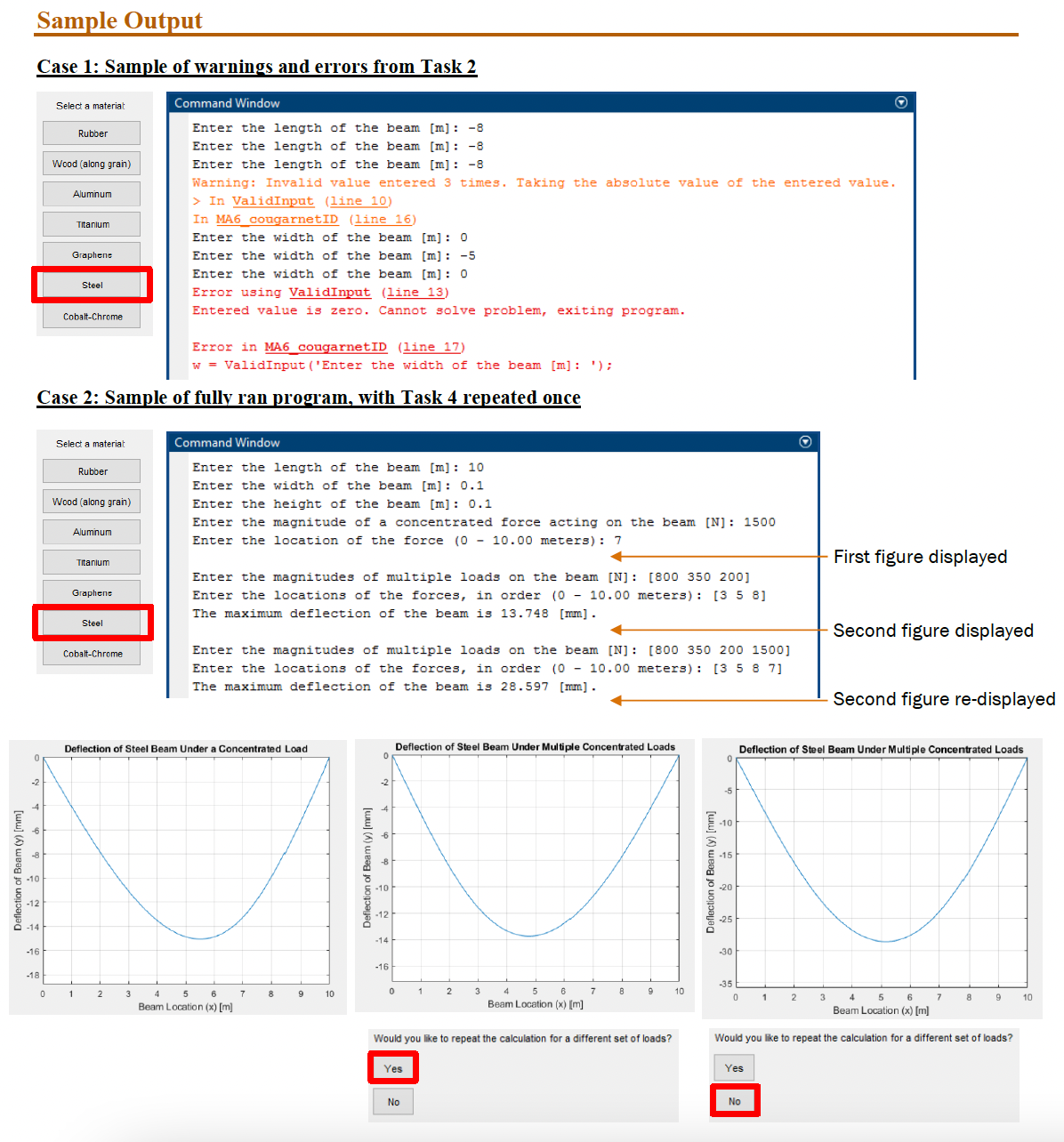
This problem will introduce you to an example of a simply supported beam subject to a load modeled as a point force. The background provides all of the equations and variable definitions needed to achieve the tasks described. Below represents a simply supported beam of length I subject to a force F. F The beam has a width w and height. The beam also has a Young's modulus, E, which represents the ability of a material to withstand changes in length (sometimes referred to as modulus of elasticity). A data file (MaterialElasticity.mat) is provided that contains materials with associated Young's moduli. For a single force the deflection of the beam is determined using the derived equation Rx 6EI Rx3 6EI y(x) = wh 12 -0x + Fa 6EIL -8x + (x-a), where I is the area moment of inertia of the cross section, R is the reaction force on the beam at the left end, and 8 is the clockwise rotational angle of the beam at the left end. These have already been derived for you and are given by the following equations: 1 = R = (L-a) 0 = P 6EI - x a Eq. 2 Eq. 3 Eq. 4 Following the tasks below, you will develop a program that will calculate the deflection of this simply supported beam with one or more loads for any beam material, dimensions and loading. You may assume that the given values will always be in SI units; this implies that the deflection equation above will calculate the deflection in meters. See MA5_SampleCalculations.pdf for examples of these beam deflection calculations. Tasks TASK 1: Material selection and data validation (3 - 5 min) Prompt the user to select a material from the Material string array. If user exits out of the menu, keep asking the user for a selection until one is made. You will use this selection to determine the Young's modulus value from the Elasticity vector. Each material has a corresponding Young's modulus [Pa]. Proficiency Time: 50 - 70 min TASK 2: Dimensional information and data validation (13 17 min) Write a user-defined function named ValidInput.m which validates a user's input. This function should use the same syntax as the built-in input() function with one input (the prompt) and one output (the stored variable). In the function, perform the following data validation: if the entered value is zero or negative, prompt the user for a new value. If after 3 attempts the user has not entered a positive value, produce a warning and take the absolute value of the most recently entered value. If the most recent value is zero, produce an error and terminate the program. Call this function 3 times in your main script to prompt the user for the length L [m], the width w [m], and the height h [m] of the beam. TASK 3: Calculate deflection for a single load on a simply supported beam (18 24 min) Prompt the user to enter a concentrated force F [N] and the location of the force on the beam a [m]. Include the length of the beam L in the statement requesting the location of the force. Using Eq. 1 through 4, determine the deflection curve across the entire beam and plot the deflection as a solid line. Your plot must include the following: X-axis label X-axis limit set to the length of the beam Title with material name Gridlines Y-axis label Deflection shown in millimeters HINT: See MA5_SampleCalculations.pdf for an example of using Eq. 1 through 4 to determine the deflection at a single point on the beam. This calculation can be generalized to apply to the entire beam. TASK 4: Calculate deflection for multiple loads on a simply supported beam (13 19 min) Prompt the user to enter multiple concentrated forces [N/m] and the locations of each of the forces on the beam [m] as vectors. Using Eq. 1 through Eq. 4, determine the total deflection of the beam caused by all of the forces across the entire beam and plot the deflection as a solid line in a new figure. Your plot should include the same formatting as the plot in Task 3. Then, output to the command window the maximum deflection of the beam in millimeters. HINT: The total deflection of the beam at any point is the sum of the deflections caused by each single force at that point. TASK 5: Programming controls (3 5 min) After Task 4, ask the user if they would like to repeat the multiple loads calculation with different forces and locations. If yes, repeat Task 4. If not, your program should end. Deflection of Beam (y) [mm] Sample Output Case 1: Sample of warnings and errors from Task 2 -10 -12 -14 -16 -18 Select a material 0 Rubber Wood (along grain) Aluminum Error in MA6 cougarnetID (line 17) w = ValidInput ('Enter the width of the beam [m] : '); Case 2: Sample of fully ran program, with Task 4 repeated once Titanium Graphene Steel Cobalt-Chrome Select a material Rubber Wood (along grain) Aluminum 1 Titanium Graphene Steel Cobalt-Chrome Command Window Enter the length of the beam [m]: -8 Enter the length of the beam [m]: -8 Enter the length of the beam [m]: -8 Warning: Invalid value entered 3 times. Taking the absolute value of the entered value. > In ValidInput (line 10) In MA6 cougarnetID (line 16) Enter the width of the beam [m]: 0 Enter the width of the beam [m]: -5 Enter the width of the beam [m]: 0 Error using ValidInput (line 13) Entered value is zero. Cannot solve problem, exiting program. 2 Command Window Enter the length of the beam [m]: 10 Enter the width of the beam [m]: 0.1 Enter the height of the beam [m]: 0.1 Enter the magnitude of a concentrated force acting on the beam [N]: 1500 Enter the location of the force (0 - 10.00 meters): 7 Enter the magnitudes of multiple loads on the beam [N]: [800 350 200] Enter the locations of the forces, in order (0 - 10.00 meters): [358] The maximum deflection of the beam is 13.748 [mm]. Deflection of Steel Beam Under a Concentrated Load Enter the magnitudes of multiple loads on the beam [N]: [800 350 200 1500] Enter the locations of the forces, in order (0-10.00 meters): [3 5 8 7] The maximum deflection of the beam is 28.597 [mm]. 6 5 Beam Location (x) [m] 7 8 9 10 Deflection of Beam (y) [mm] -12 -14 Deflection of Steel Beam Under Multiple Concentrated Loads -16- 0 Yes 1 No 2 3 4 6 Beam Location (x) [m] 7 8 Would you like to repeat the calculation for a different set of loads? 9 10 Deflection of Beam (y) [mm] 0 -10 -30 -35 0 Yes Deflection of Steel Beam Under Multiple Concentrated Loads No O 2 4 5 6 Beam Location (x) [m] Would you like to repeat the calculation for a different set of loads? First figure displayed 3 Second figure displayed Second figure re-displayed 7 8 9