This project is about binary search tree

just copy these codes and paste them if you need to use the hints that made by my professor. I typed (file name).py to easier to recognize.

main.py

from pathlib import Path from string import whitespace, punctuation from bst import BST

class Pair:

''' Encapsulate letter,count pair as a single entity.

Realtional methods make this object comparable

using built-in operators.

'''

def __init__(self, letter: str, count = 1):

self.letter = letter

self.count = count

def __eq__(self, other: 'Pair'):

return self.letter == other.letter

def __hash__(self):

return hash(self.letter)

def __ne__(self, other: 'Pair'):

return self.letter != other.letter

def __lt__(self, other: 'Pair'):

return self.letter

def __le__(self, other: 'Pair'):

return self.letter

def __gt__(self, other: 'Pair'):

return self.letter > other.letter

def __ge__(self, other: 'Pair'):

return self.letter >= other.letter

def __repr__(self):

return f'({self.letter}, {self.count})'

def __str__(self):

return f'({self.letter}, {self.count})'

def make_tree() -> 'BST':

''' A helper function to build the tree.

The test code depends on this function being available from main.

:param: None

:returns: A binary search tree

'''

pass

def main():

''' Program kicks off here.

# read the file

# add each character `Pair(char.lower())` to the tree

'''

pass

if __name__ == "__main__":

main()

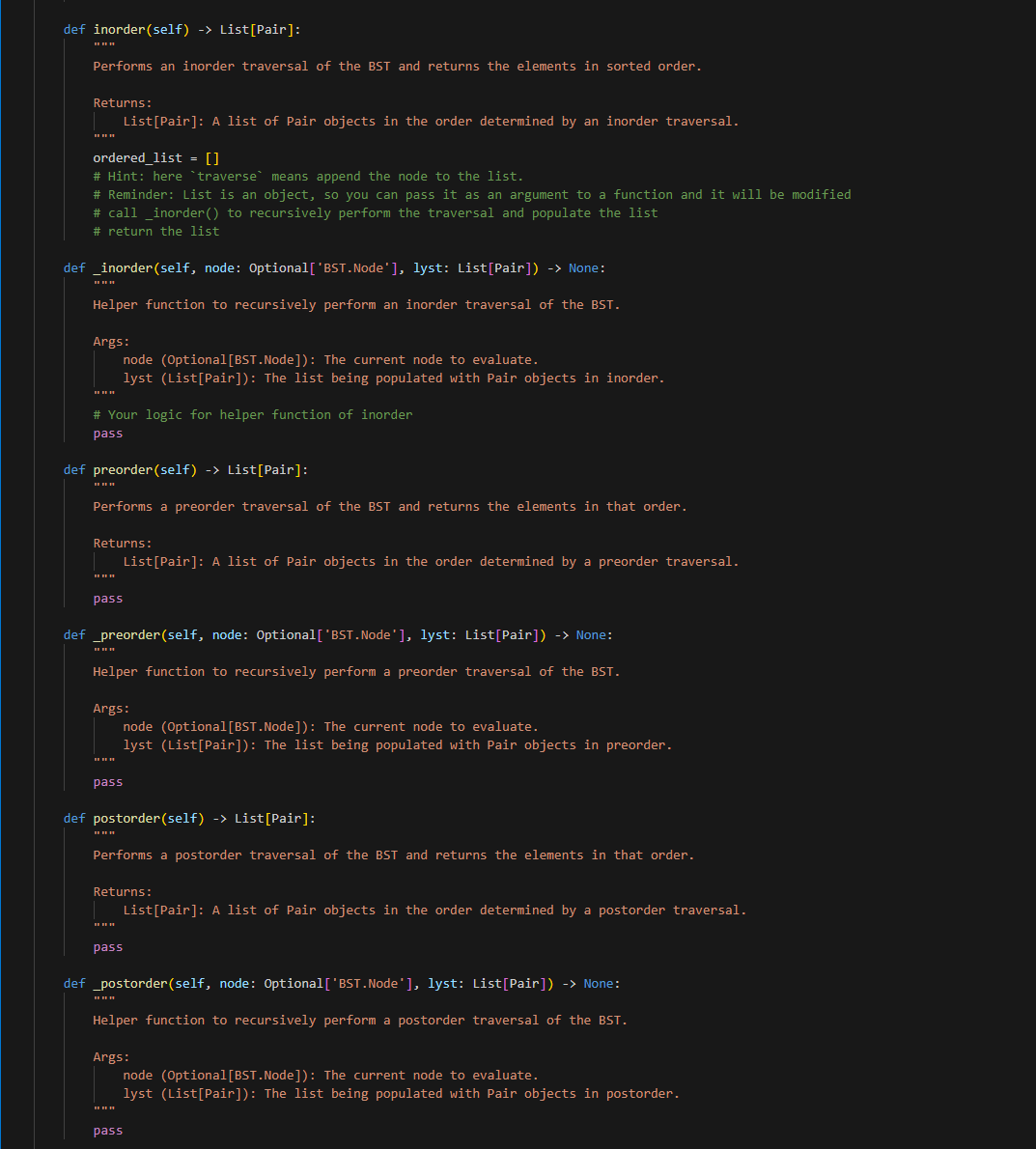
This is bst.py it's long hints to code for me.. I did but I failed.. here is the screenshot made by my professor.

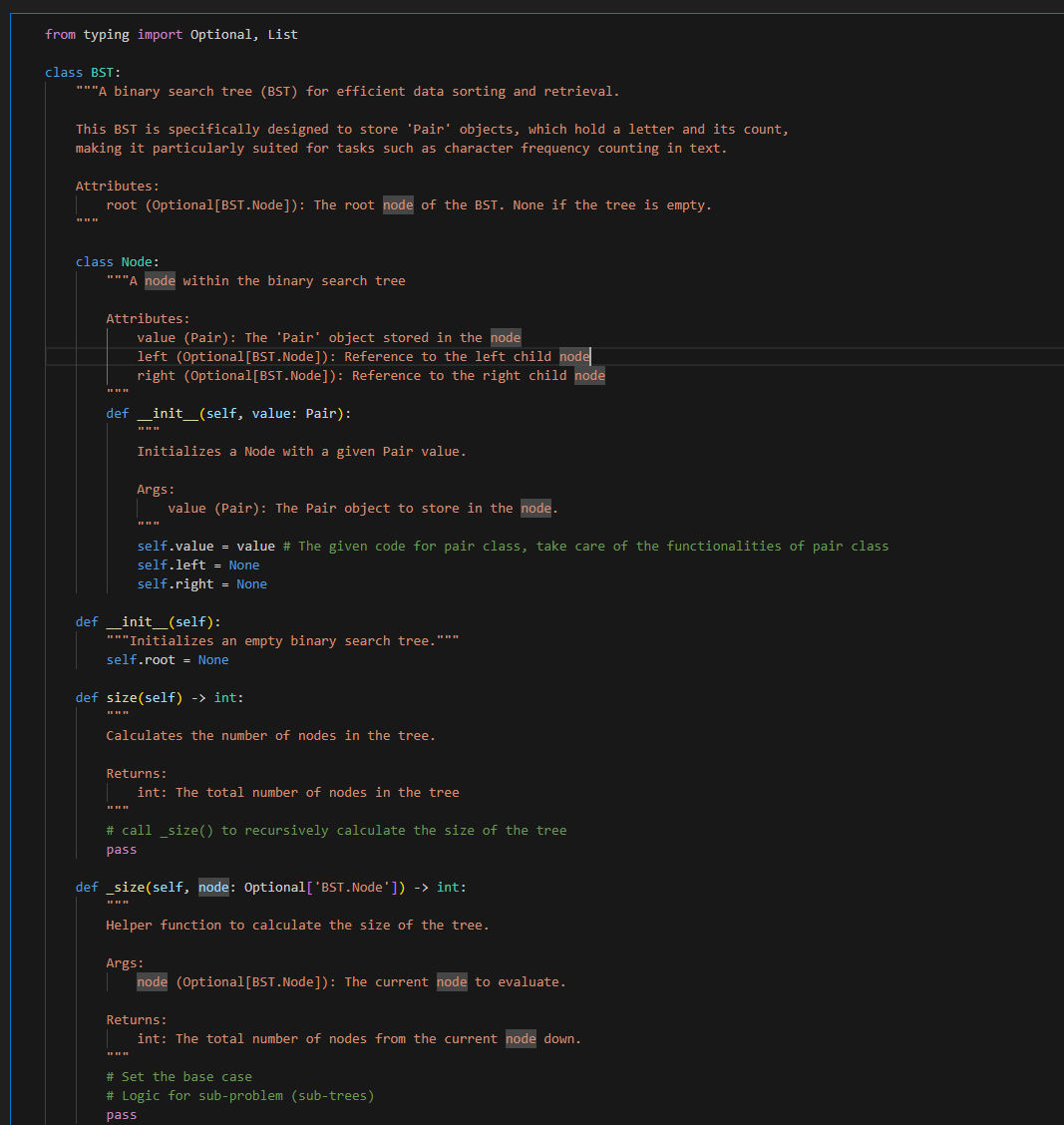
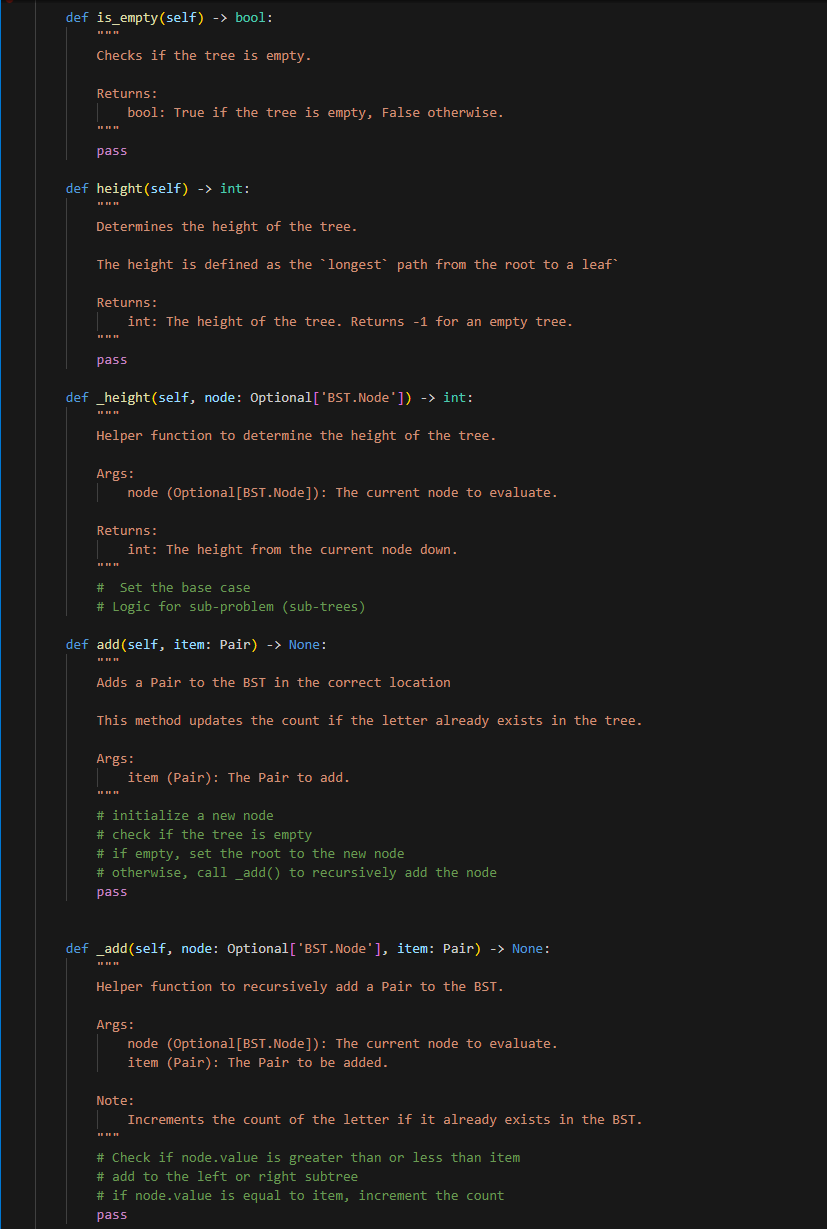
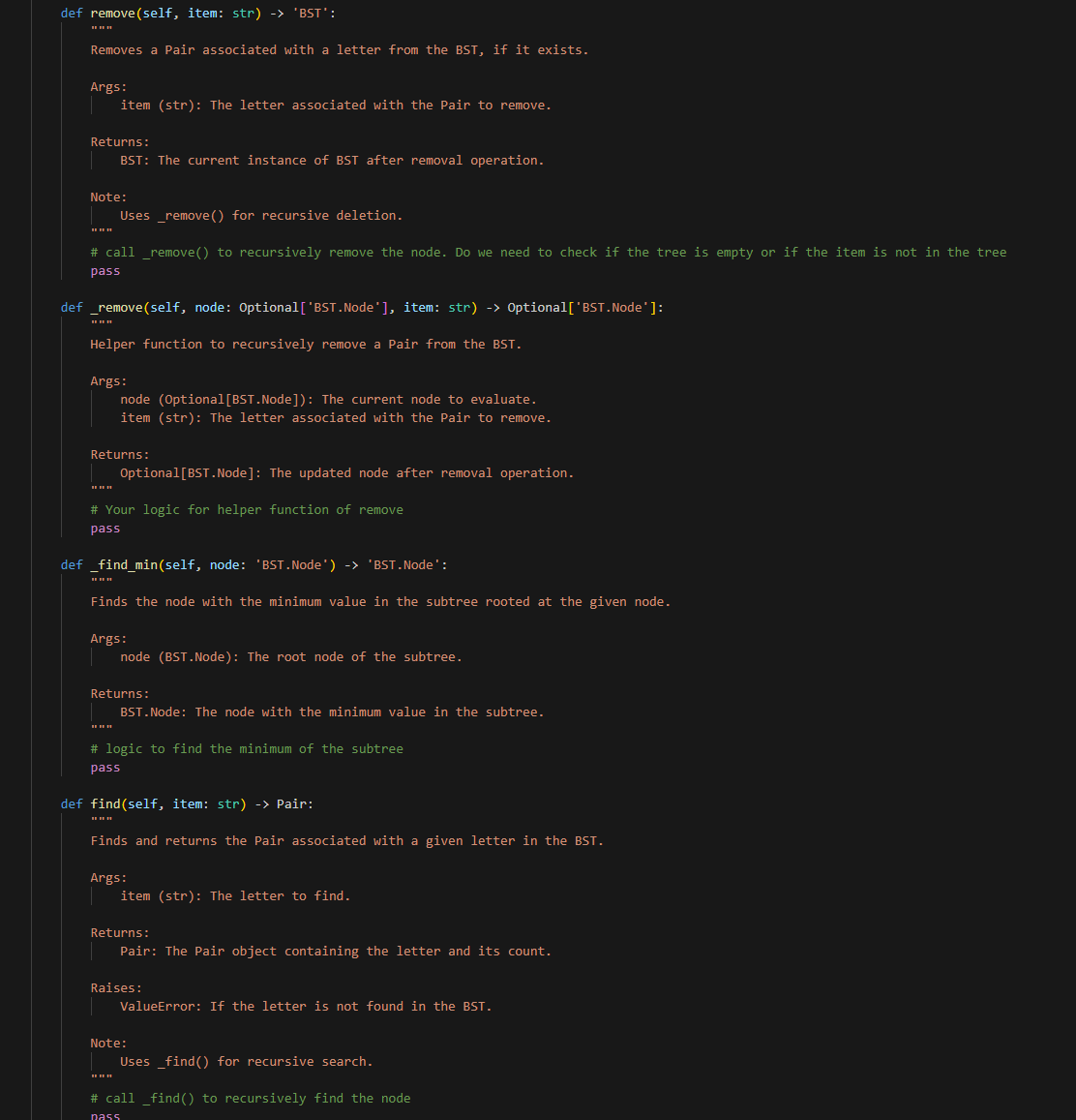
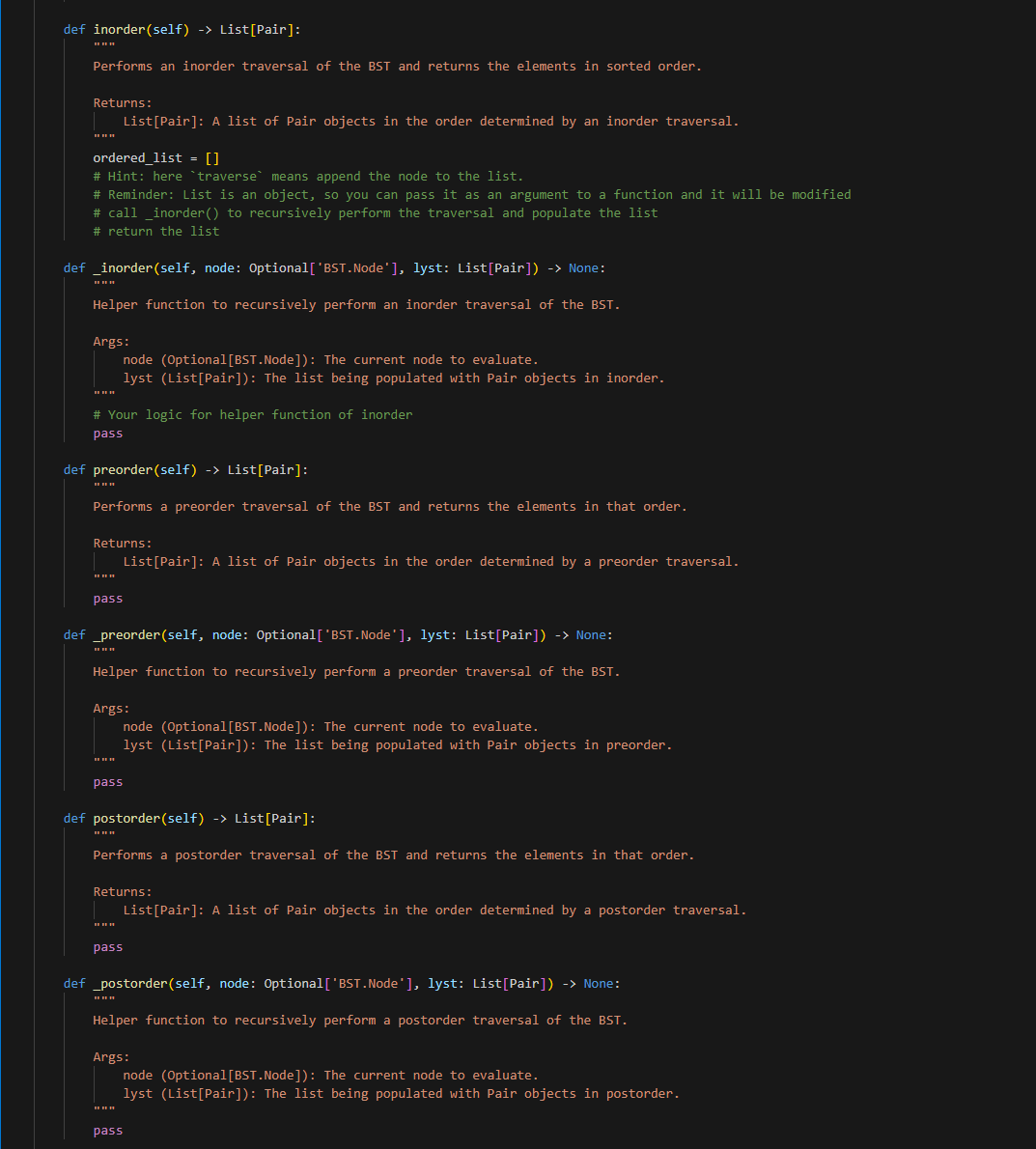
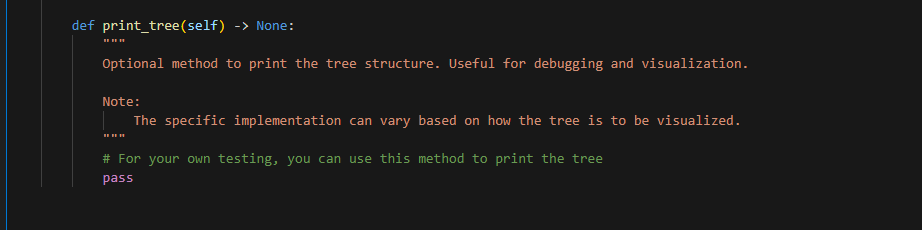
def inorder(self) List [Pair]: " " " Performs an inorder traversal of the BST and returns the elements in sorted order. Returns: List[Pair]: A list of Pair objects in the order determined by an inorder traversal. "n" ordered_list =[] \# Hint: here "traverse" means append the node to the list. \# Reminder: List is an object, so you can pass it as an argument to a function and it will be modified \# call_inorder() to recursively perform the traversal and populate the list \# return the list def _inorder(self, node: Optional['BST.Node'], lyst: List[Pair]) None: Helper function to recursively perform an inorder traversal of the BST. Args: node (Optional[BST.Node]): The current node to evaluate. lyst (List[Pair]): The list being populated with Pair objects in inorder. " "n \# Your logic for helper function of inorder pass def preorder(self) List [Pair]: "n Performs a preorder traversal of the BST and returns the elements in that order. Returns : List[Pair]: A list of Pair objects in the order determined by a preorder traversal. pass def _preorder(self, node: Optional['BST.Node'], lyst: List[Pair]) -> None: "r "n Helper function to recursively perform a preorder traversal of the BST. Args: node (Optional[BST.Node]): The current node to evaluate. lyst (List[Pair]): The list being populated with Pair objects in preorder. pass def postorder(self) List [Pair]: Performs a postorder traversal of the BST and returns the elements in that order. Returns: List[Pair]: A list of Pair objects in the order determined by a postorder traversal. pass def _postorder(self, node: Optional['BST.Node'], lyst: List[Pair]) -> None: "in Helper function to recursively perform a postorder traversal of the BST. Args: node (Optional[BST.Node]): The current node to evaluate. lyst (List[Pair]): The list being populated with Pair objects in postorder. "n" pass Part 1: BST Not surprisingly, your first task will be to create a binary search tree ADT as a class called BST. You should implement this class in a file called bst.py. Your ADT must implement the following methods: - size(): Return the number of nodes in the tree. - is_empty(): Return True if there aren't any nodes in the tree, False otherwise. - height(): Return the height of the tree, defined is the length of the path from the root to its deepest leaf. A tree with zero nodes has a height of -1 . - add(item): Add item to its proper place in the tree. Return the modified tree. - remove(item): Remove item from the tree if it exists, if not - do nothing. Return the resulting tree. - find(item): Return the matched item from the tree (not the node that contains it, and not the item used as the parameter). If item is not in the tree, raise a ValueError. - inorder(): Return a list with the data items in order of inorder traversal. - preorder(): Return a list with the data items in order of preorder traversal. - postorder(): Return a list with the data items in order of postorder traversal. - [Optional] print_tree(): print the values in the tree (in any way you wish). Useful for debugging purposes (a good example of this can be found in section 5.12.1 under the TreePrint.py file). Your BST class must be generic is the sense that it can store and operate on any kind of data items that are comparable. For instance it should be possible to store a set of integers in one instance of your BST class, and a set of strings in another (without modification). Part 2: Counting with trees For part 2 of this project you are to use your BST to count the occurrence of letters in a sample test file (note: for our purposes we will NOT consider whitespace characters - you should ignore tabs, spaces, and newlines). To do this you will need to be able to store both a character and its current count in the tree. One way to do this is to utilize a simple class that stores both of these values, and is comparable on one of them (i.e. you can compare objects of the class using > int: "n" Calculates the number of nodes in the tree. Returns: int: The total number of nodes in the tree \# call_size() to recursively calculate the size of the tree pass def _size(self, node: Optional['BST.Node']) int: Helper function to calculate the size of the tree. Args: node (Optional[BST.Node]): The current node to evaluate. Returns: int: The total number of nodes from the current node down. n"n \# Set the base case \# Logic for sub-problem (sub-trees) pass def is_empty(self) bool: Checks if the tree is empty. Returns: bool: True if the tree is empty, False otherwise. "n" pass def height(self) int: " "n Determines the height of the tree. The height is defined as the 'longest' path from the root to a leaf' Returns: int: The height of the tree. Returns -1 for an empty tree. "."." pass def_height(self, node: Optional['BST.Node']) -> int: Helper function to determine the height of the tree. Args: node (Optional[BST.Node]): The current node to evaluate. Returns: int: The height from the current node down. " " " " \# Set the base case \# Logic for sub-problem (sub-trees) def add(self, item: Pair) -> None: "n " Adds a Pair to the BST in the correct location This method updates the count if the letter already exists in the tree. Args: item (Pair): The Pair to add. "n" \# initialize a new node \# check if the tree is empty \# if empty, set the root to the new node \# otherwise, call_add() to recursively add the node pass def _add(self, node: Optional['BST.Node'], item: Pair) None: "n." Helper function to recursively add a Pair to the BST. Args: node (Optional[BST.Node]): The current node to evaluate. item (Pair): The Pair to be added. Note: Increments the count of the letter if it already exists in the BST. "n." \# Check if node.value is greater than or less than item \# add to the left or right subtree \# if node.value is equal to item, increment the count pass def remove(self, item: str) 'BST': " " " Removes a Pair associated with a letter from the BST, if it exists. Args: item (str): The letter associated with the Pair to remove. Returns: BST: The current instance of BST after removal operation. Note: Uses_remove() for recursive deletion. in \# call_remove() to recursively remove the node. Do we need to check if the tree is empty or if the item is not in the tree pass def _remove(self, node: Optional['BST.Node'], item: str) Optional['BST.Node']: Helper function to recursively remove a Pair from the BST. Args: node (Optional[BST.Node]): The current node to evaluate. item (str): The letter associated with the Pair to remove. Returns: Optional[BST.Node]: The updated node after removal operation. \# Your logic for helper function of remove pass def _find_min(self, node: 'BST.Node') 'BST.Node': - + in Finds the node with the minimum value in the subtree rooted at the given node. Args: node (BST.Node): The root node of the subtree. Returns: BST.Node: The node with the minimum value in the subtree. \# logic to find the minimum of the subtree pass def find(self, item: str) Pair: "n" Finds and returns the Pair associated with a given letter in the BST. Args: item (str): The letter to find. Returns: Pair: The Pair object containing the letter and its count. Raises: ValueError: If the letter is not found in the BST. Note: Uses_find() for recursive search. nn" \# call_find() to recursively find the node def inorder(self) List [Pair]: " " " Performs an inorder traversal of the BST and returns the elements in sorted order. Returns: List[Pair]: A list of Pair objects in the order determined by an inorder traversal. "n" ordered_list =[] \# Hint: here "traverse" means append the node to the list. \# Reminder: List is an object, so you can pass it as an argument to a function and it will be modified \# call_inorder() to recursively perform the traversal and populate the list \# return the list def _inorder(self, node: Optional['BST.Node'], lyst: List[Pair]) None: Helper function to recursively perform an inorder traversal of the BST. Args: node (Optional[BST.Node]): The current node to evaluate. lyst (List[Pair]): The list being populated with Pair objects in inorder. " "n \# Your logic for helper function of inorder pass def preorder(self) List [Pair]: "n Performs a preorder traversal of the BST and returns the elements in that order. Returns : List[Pair]: A list of Pair objects in the order determined by a preorder traversal. pass def _preorder(self, node: Optional['BST.Node'], lyst: List[Pair]) -> None: "r "n Helper function to recursively perform a preorder traversal of the BST. Args: node (Optional[BST.Node]): The current node to evaluate. lyst (List[Pair]): The list being populated with Pair objects in preorder. pass def postorder(self) List [Pair]: Performs a postorder traversal of the BST and returns the elements in that order. Returns: List[Pair]: A list of Pair objects in the order determined by a postorder traversal. pass def _postorder(self, node: Optional['BST.Node'], lyst: List[Pair]) -> None: "in Helper function to recursively perform a postorder traversal of the BST. Args: node (Optional[BST.Node]): The current node to evaluate. lyst (List[Pair]): The list being populated with Pair objects in postorder. "n" pass def print_tree(self) None: " " Optional method to print the tree structure. Useful for debugging and visualization. Note: The specific implementation can vary based on how the tree is to be visualized. "n" \# For your own testing, you can use this method to print the tree pass