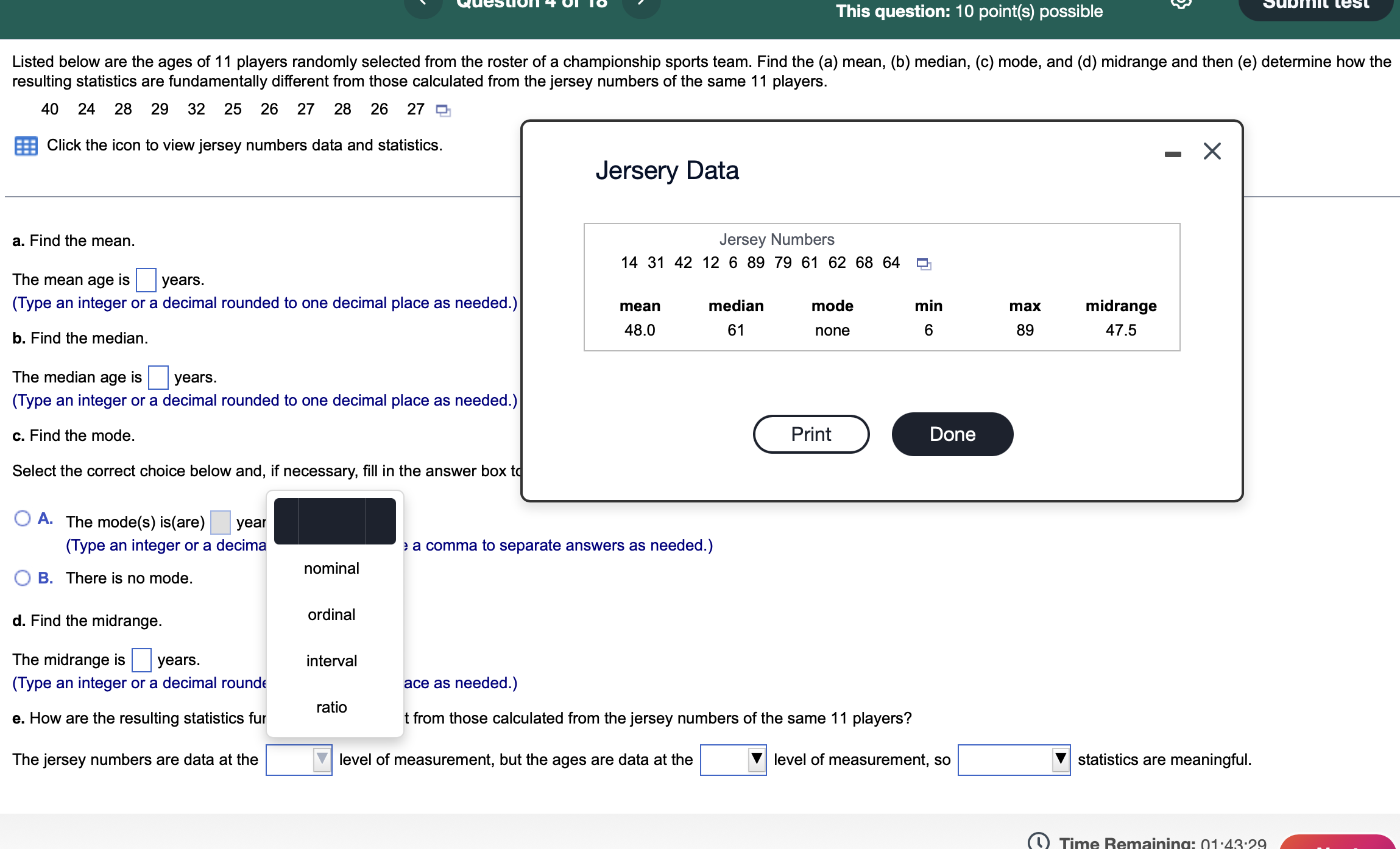
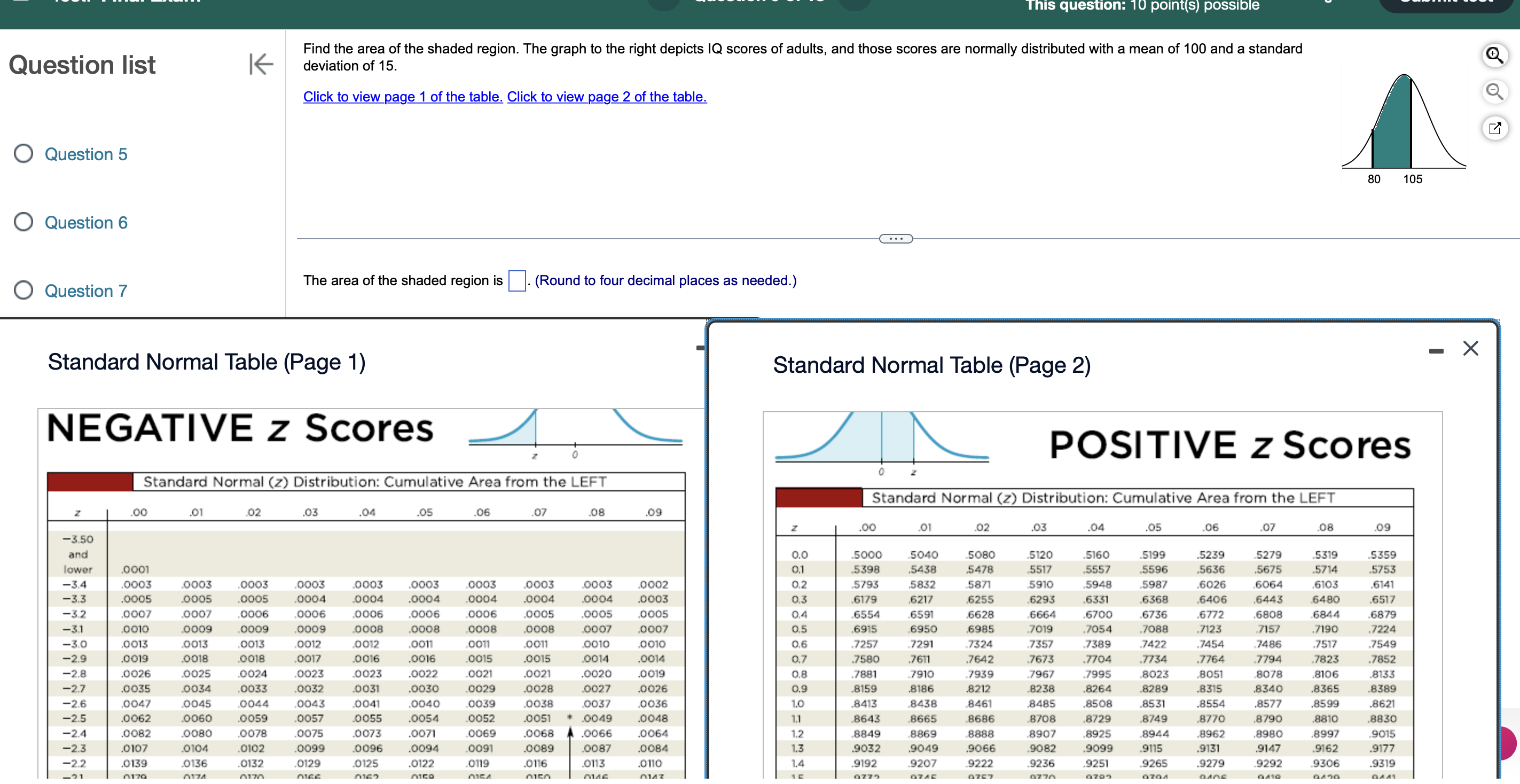
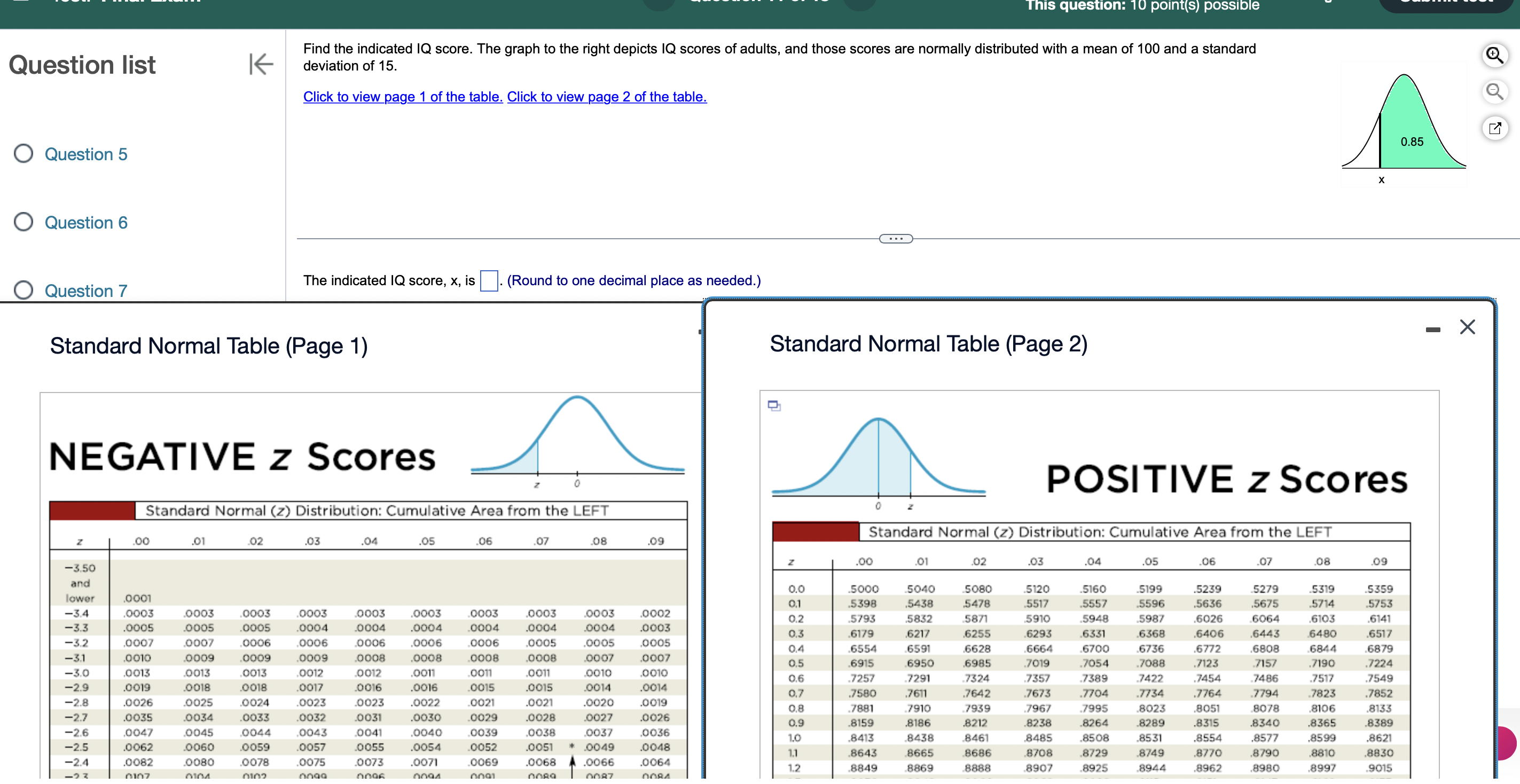
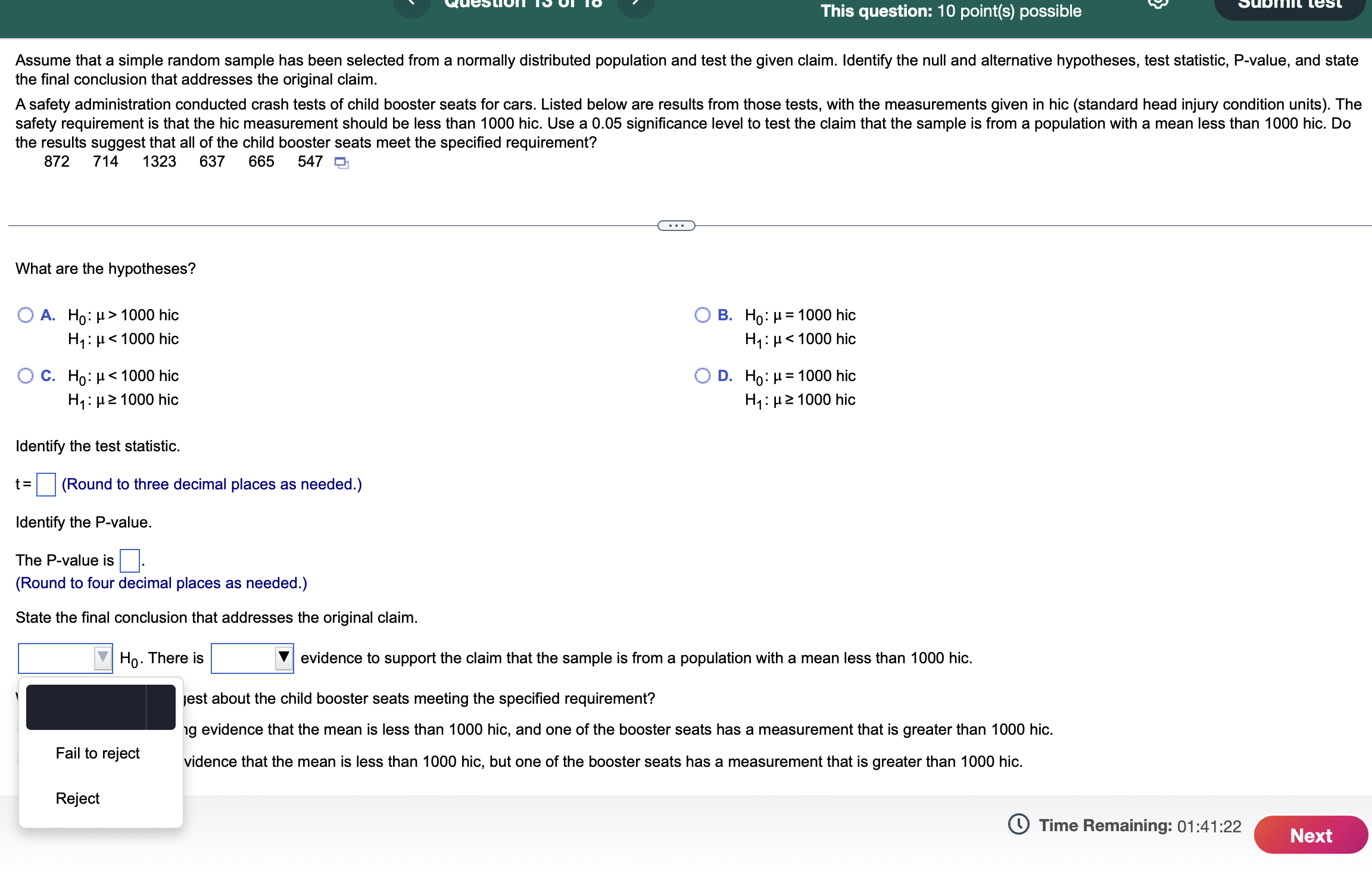
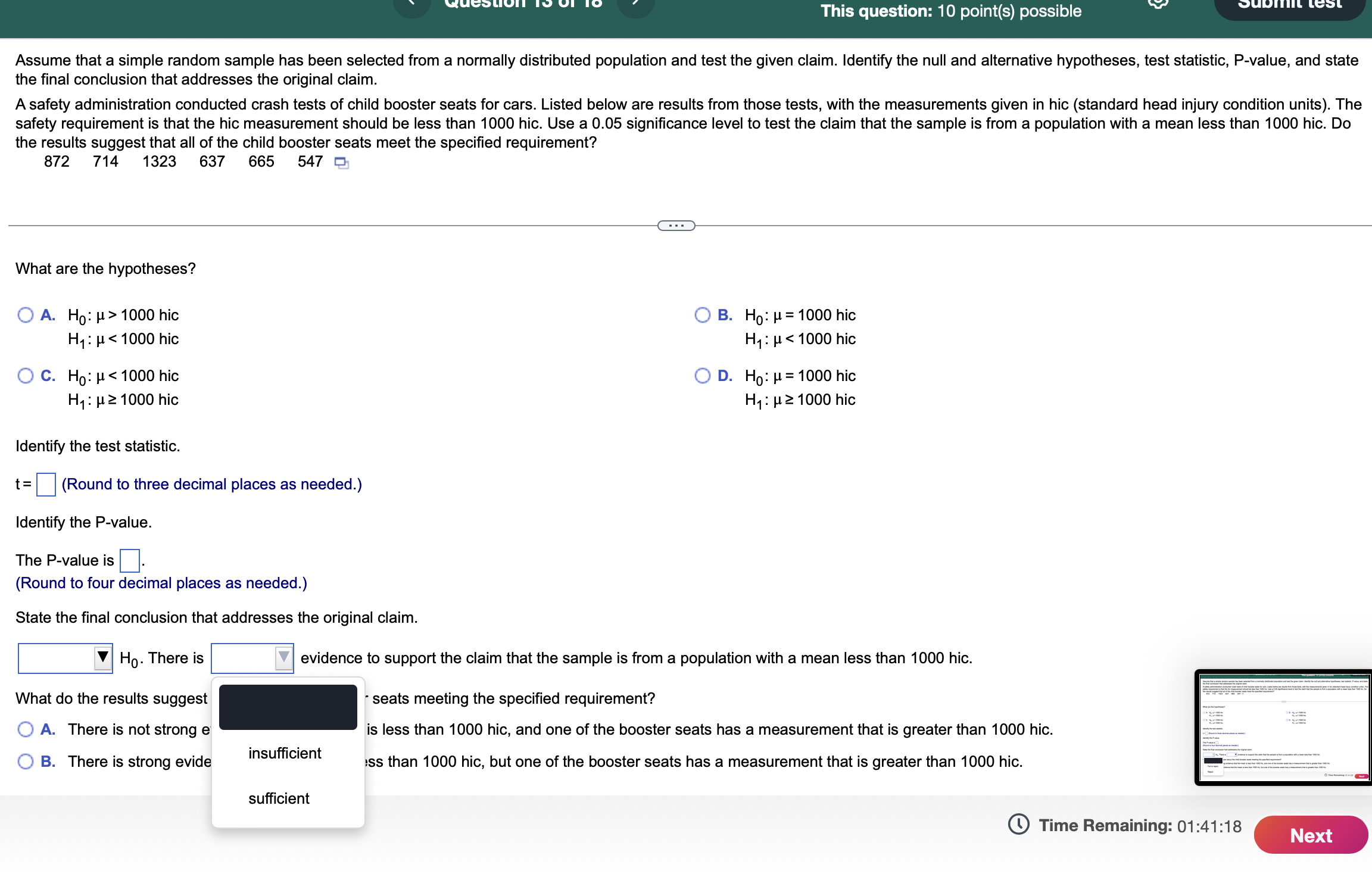
This question: 10 point(s) possible Listed below are the ages of 11 players randomly selected from the roster of a championship sports team. Find the (a) mean, (b) median, (c) mode, and (d) midrange and then (e) determine how the resulting statistics are fundamentally different from those calculated from the jersey numbers of the same 11 players. 40 24 28 29 32 25 26 27 28 26 27 Click the icon to view jersey numbers data and statistics. - a. Find the mean. The mean age is years. Jersery Data Jersey Numbers 14 31 42 12 6 89 79 61 62 68 64 (Type an integer or a decimal rounded to one decimal place as needed.) mean 48.0 median 61 mode min max none 6 89 midrange 47.5 b. Find the median. The median age is years. (Type an integer or a decimal rounded to one decimal place as needed.) c. Find the mode. Select the correct choice below and, if necessary, fill in the answer box to Print Done A. The mode(s) is (are) year (Type an integer or a decima > a comma to separate answers as needed.) nominal B. There is no mode. d. Find the midrange. ordinal The midrange is years. interval (Type an integer or a decimal rounde e. How are the resulting statistics fur ace as needed.) ratio t from those calculated from the jersey numbers of the same 11 players? The jersey numbers are data at the level of measurement, but the ages are data at the level of measurement, so statistics are meaningful. Time Remaining: 01:43:29 This question: 10 point(s) possible Find the area of the shaded region. The graph to the right depicts IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15. Question list K Click to view page 1 of the table. Click to view page 2 of the table. Question 5 Question 6 Question 7 The area of the shaded region is (Round to four decimal places as needed.) Standard Normal Table (Page 1) NEGATIVE z Scores Z 0 Standard Normal Table (Page 2) 80 105 POSITIVE z Scores 0 Z Standard Normal (z) Distribution: Cumulative Area from the LEFT Standard Normal (z) Distribution: Cumulative Area from the LEFT .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 Z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 -3.50 and 0.0 .5000 .5040 5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359 lower .0001 0.1 .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 -3.4 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0002 0.2 .5793 .5832 .5871 5910 .5948 .5987 .6026 .6064 .6103 .6141 -3.3 .0005 .0005 .0005 .0004 .0004 .0004 .0004 .0004 .0004 .0003 0.3 .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 -3.2 .0007 .0007 .0006 .0006 .0006 .0006 .0006 .0005 .0005 .0005 0.4 .6554 .6591 .6628 .6664 .6700 .6736 .6772 .6808 .6844 .6879 -3.1 .0010 .0009 .0009 .0009 .0008 .0008 .0008 .0008 .0007 .0007 0.5 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 -3.0 .0013 .0013 .0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 0.6 .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 -2.9 .0019 .0018 .0018 .0017 .0016 .0016 .0015 .0015 .0014 .0014 0.7 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 -2.8 .0026 .0025 .0024 .0023 .0023 .0022 .0021 .0021 .0020 .0019 0.8 .7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 -2.7 .0035 .0034 .0033 .0032 .0031 .0030 .0029 .0028 .0027 .0026 0.9 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389 -2.6 .0047 .0045 .0044 .0043 .0041 .0040 .0039 .0038 .0037 .0036 1.0 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 -2.5 .0062 .0060 .0059 .0057 .0055 .0054 .0052 .0051 * .0049 .0048 1.1 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830 -2.4 .0082 .0080 .0078 .0075 .0073 .0071 .0069 .0068 .0066 .0064 1.2 .8849 .8869 8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015 -2.3 .0107 0104 .0102 .0099 .0096 .0094 .0091 .0089 .0087 .0084 1.3 .9032 .9049 .9066 .9082 .9099 .9115 .9131 .9147 .9162 .9177 -2.2 .0139 .0136 .0132 .0129 .0125 .0122 .0119 .0116 .0113 .0110 1.4 .9192 .9207 .9222 .9236 .9251 .9265 .9279 .9292 .9306 .9319 -21 0179 0174 0170 0166 0162 0150 0154 0150 0116 0147 15 OZZO OZA5 0757 0770 QZ02 0701 0106 0419 0130 0411 This question: 10 point(s) possible Find the indicated IQ score. The graph to the right depicts IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15. Question list K Click to view page 1 of the table. Click to view page 2 of the table. Question 5 Question 6 Question 7 The indicated IQ score, x, is (Round to one decimal place as needed.) Standard Normal Table (Page 1) NEGATIVE z Scores ... Standard Normal Table (Page 2) 0.85 POSITIVE z Scores Standard Normal (z) Distribution: Cumulative Area from the LEFT Z .00 .01 .02 .03.04 .05 .06 .07 .08 .09 0 z Standard Normal (z) Distribution: Cumulative Area from the LEFT Z .00 .01 .02 .03 -3.50 .04 .05 .06 .07 .08 .09 and 0.0 .5000 5040 .5080 .5120 .5160 5199 .5239 .5279 .5319 .5359 lower .0001 0.1 .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 -3.4 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0002 0.2 .5793 .5832 .5871 5910 .5948 .5987 .6026 .6064 .6103 .6141 -3.3 .0005 .0005 .0005 .0004 .0004 .0004 .0004 .0004 .0004 .0003 0.3 .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 -3.2 .0007 .0007 .0006 .0006 .0006 .0006 .0006 .0005 .0005 .0005 0.4 .6554 .6591 .6628 .6664 .6700 .6736 .6772 .6808 .6844 .6879 -3.1 .0010 .0009 .0009 .0009 .0008 .0008 .0008 .0008 .0007 .0007 0.5 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 -3.0 .0013 .0013 .0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 0.6 .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 -2.9 .7517 .7549 .0019 .0018 .0018 .0017 .0016 .0016 .0015 .0015 .0014 .0014 0.7 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 -2.8 .0026 .7852 .0025 .0024 .0023 .0023 .0022 .0021 .0021 .0020 .0019 0.8 .7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 -2.7 .0035 .0034 .0033 .0032 .0031 .0030 .0029 .0028 .0027 .0026 0.9 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389 -2.6 .0047 .0045 .0044 .0043 .0041 .0040 .0039 .0038 .0037 .0036 1.0 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 -2.5 .0062 .0060 .0059 .0057 .0055 .0054 .0052 .0051 * .0049 .0048 1.1 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830 -2.4 .0082 .0080 .0078 .0075 .0073 .0071 .0069 .0068 .0066 .0064 1.2 .8849 .8869 8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015 -23 0107 0104 0102 0099 0096 0094 0091 0089 0087 0084 - This question: 10 point(s) possible Assume that a simple random sample has been selected from a normally distributed population and test the given claim. Identify the null and alternative hypotheses, test statistic, P-value, and state the final conclusion that addresses the original claim. A safety administration conducted crash tests of child booster seats for cars. Listed below are results from those tests, with the measurements given in hic (standard head injury condition units). The safety requirement is that the hic measurement should be less than 1000 hic. Use a 0.05 significance level to test the claim that the sample is from a population with a mean less than 1000 hic. Do the results suggest that all of the child booster seats meet the specified requirement? 872 714 1323 637 665 547 What are the hypotheses? A. Ho >1000 hic H: