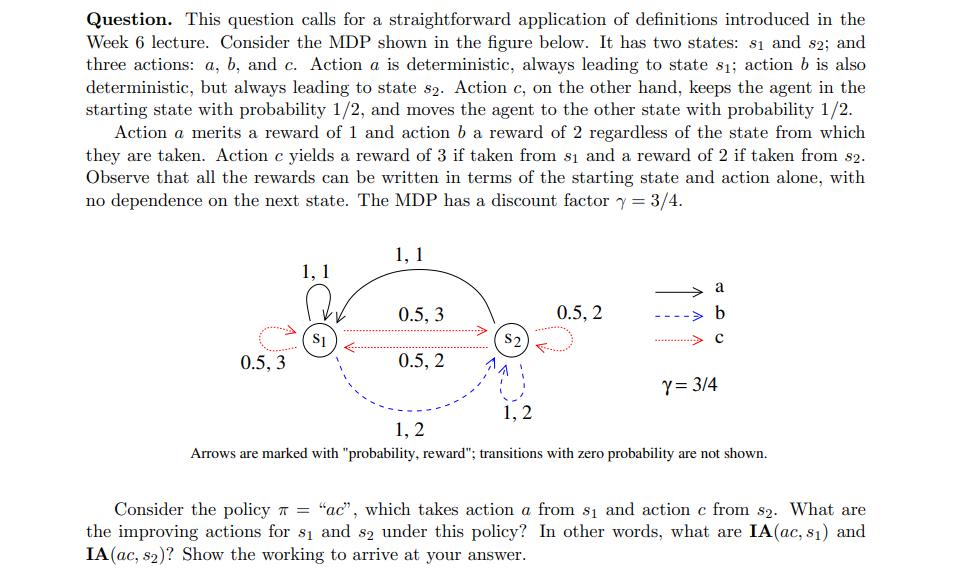
This question calls for a straightforward application of definitions introduced in the Week 6 lecture. Consider the MDP shown in the figure below. It has two states: s1 and s2; and three actions: a, b, and c. Action a is deterministic, always leading to state s; action b is also deterministic, but always leading to state s2. Action c, on the other hand, keeps the agent in the starting state with probability 1/2, and moves the agent to the other state with probability 1/2. Action a merits a reward of 1 and action b a reward of 2 regardless of the state from which they are taken. Action c yields a reward of 3 if taken from s and a reward of 2 if taken from 82. Observe that all the rewards can be written in terms of the starting state and action alone, with no dependence on the next state. The MDP has a discount factor y = 3/4. 0.5, 3 1, 1 S1 1, 1 0.5, 3 0.5, 2 $2 1, 2 0.5, 2 a b C Y = 3/4 1, 2 Arrows are marked with "probability, reward"; transitions with zero probability are not shown. Consider the policy = "ac", which takes action a from s and action c from s2. What are the improving actions for s and 82 under this policy? In other words, what are IA(ac, s) and IA (ac, s2)? Show the working to arrive at your answer.