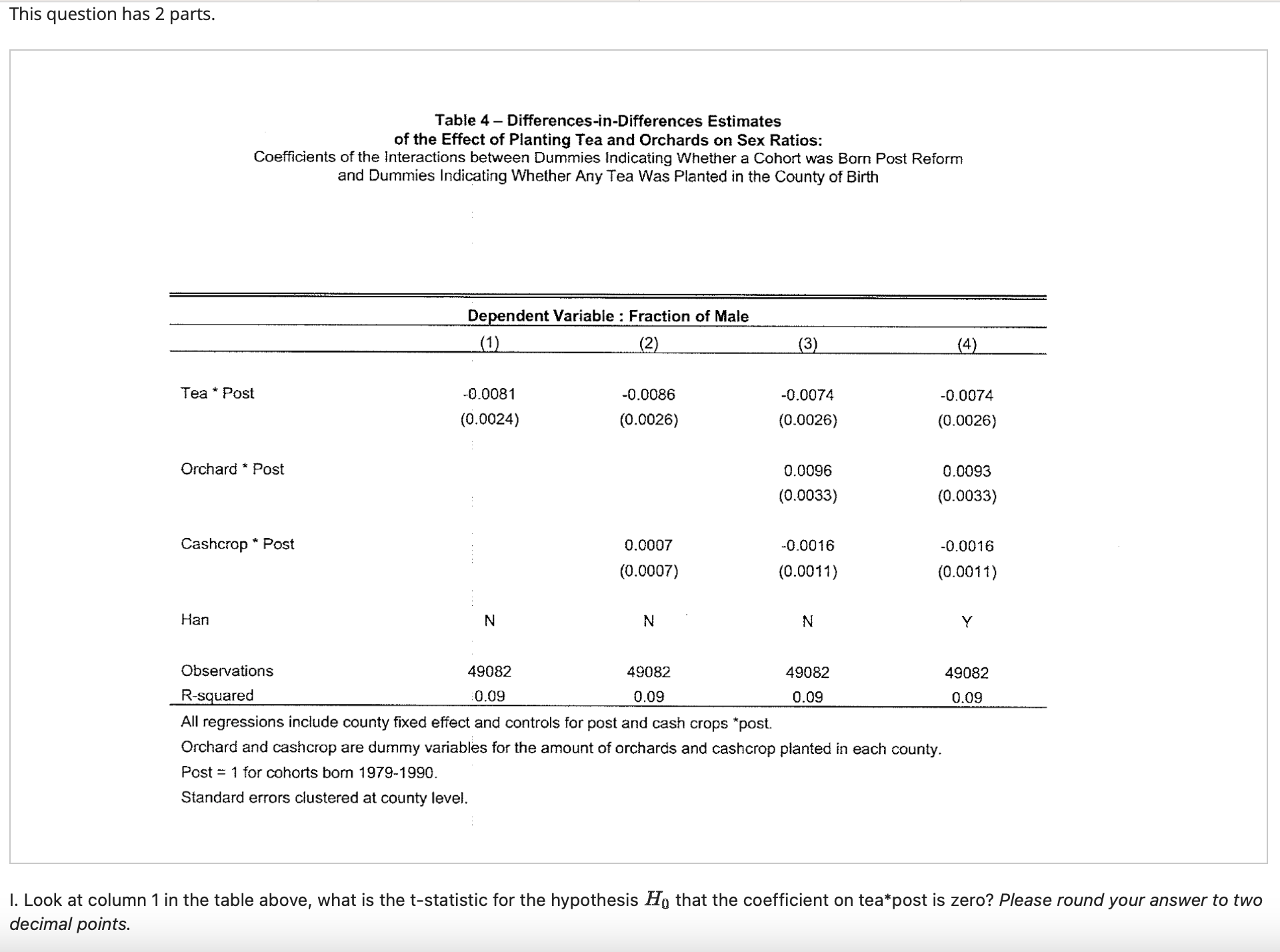
This question has 2 parts. Tea * Post Table 4-Differences-in-Differences Estimates of the Effect of Planting Tea and Orchards on Sex Ratios: Coefficients of the Interactions between Dummies Indicating Whether a Cohort was Born Post Reform and Dummies Indicating Whether Any Tea Was Planted in the County of Birth Orchard Post Cashcrop Post Han Dependent Variable: Fraction of Male (1) (2) (3) (4) -0.0081 -0.0086 -0.0074 -0.0074 (0.0024) (0.0026) (0.0026) (0.0026) 0.0096 (0.0033) 0.0093 (0.0033) 0.0007 (0.0007) -0.0016 -0.0016 (0.0011) (0.0011) N N N Y Observations 49082 R-squared 0.09 49082 0.09 49082 49082 0.09 0.09 All regressions include county fixed effect and controls for post and cash crops *post. Orchard and cashcrop are dummy variables for the amount of orchards and cashcrop planted in each county. Post 1 for cohorts born 1979-1990. Standard errors clustered at county level. I. Look at column 1 in the table above, what is the t-statistic for the hypothesis Ho that the coefficient on tea*post is zero? Please round your answer to two decimal points. Question 20 0.0/1.0 point (graded) We only observe tea production in the regions that have chosen to produce tea. Your friend who is an anthropology major argues that in some regions, people are more likely to prefer girls, for historical reasons. Could these regions then decide to grow more tea? If yes, what assumption underlying this design strategy would this violate? the independence assumption the parallel trends assumption the exclusion restriction None of the above Question 21 0.0/1.0 point (graded) To solve this problem, Qian uses the fact that some regions are more suitable to tea production than others: in particular, a certain amount of rain, elevation and slopes are needed to produce tea. She decides to propose an instrumental variables strategy. What is the first stage equation? An OLS regression of TEA on rain, elevation, and slope. An OLS regression of the fraction of boys on rain, elevation, and slope. An OLS regression of TEA on rain, elevation, and slope with fixed effects. An OLS regression of the fraction of boys on rain, elevation, and slope including region fixed effects and a dummy for whether or not the country grows Orchards. Question 22 0.0/1.0 point (graded) What assumptions are needed for the instrument to be a good instrument? Rain, elevation, and slope don't affect the fraction of boys except through tea growth. Rain, elevation, and slope affect whether or not a region grows tea. Rain, elevation, and slope vary randomly across regions that grow tea and regions that don't. All of the above.