Answered step by step
Verified Expert Solution
Question
1 Approved Answer
This question is a compound true/false question with 8 questions. The answers to 4 of these are true or correct and the answers to

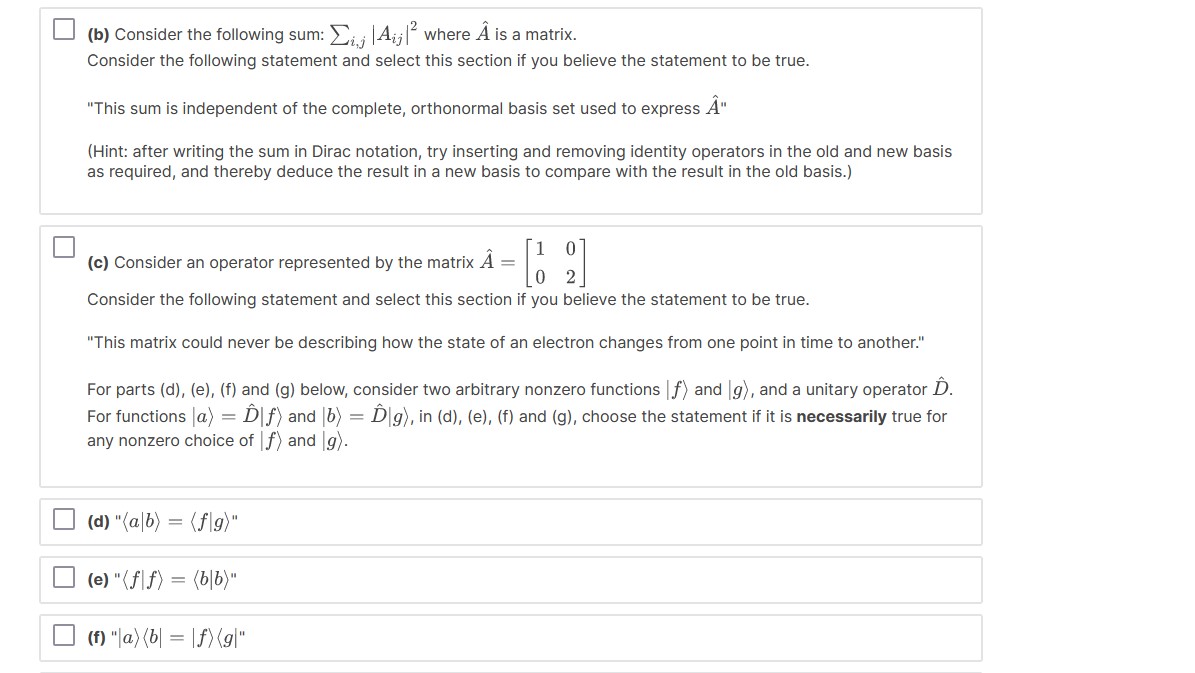

This question is a compound true/false question with 8 questions. The answers to 4 of these are true or correct and the answers to the other 4 are false or incorrect. Choose only the 4 "true" ones. (Note that the grader program is not smart enough to give you any credit if you choose any number other than 4 true answers, but it will also not stop you from selecting more than 4. So, please select exactly 4 "true" answers each time you attempt this question.) (a) Consider the following matrix: 5 36-8+4i-5-10i 3- 6i 9 12i -15 = -8-4i -12i 16 20i -5 + 10i -15 -20i 25 and two vectors: 1+2i 3 = |t) = -4i 2+2i 3+2i -1 - 5i -5 Consider the following statement and select this section if you believe the statement to be true. "A has an inverse" (Hint: you do not have to formally try to evaluate the inverse of here. What effect does have on these vectors?) (b) Consider the following sum: i, Aij A where A is a matrix. Consider the following statement and select this section if you believe the statement to be true. "This sum is independent of the complete, orthonormal basis set used to express " (Hint: after writing the sum in Dirac notation, try inserting and removing identity operators in the old and new basis as required, and thereby deduce the result in a new basis to compare with the result in the old basis.) (c) Consider an operator represented by the matrix 0 1 0 2 Consider the following statement and select this section if you believe the statement to be true. "This matrix could never be describing how the state of an electron changes from one point in time to another." For parts (d), (e), (f) and (g) below, consider two arbitrary nonzero functions (f) and (g), and a unitary operator D. For functions (a) =D f) and b) = D\g), in (d), (e), (f) and (g), choose the statement if it is necessarily true for any nonzero choice of f) and g). (d) "(ab) = (fg)" (e) "(f|f) = (b|b)" (f) "|a) (b|=|fg|" (g) "(bDg)=(g|D|b)" (h) Suppose two specific Hermitian operators A and B commute. Consider the following statement and select this section if you believe it is necessarily true. "If Af) = af) and B|g) = B|g), where a and are different numbers and f) and (g) are both nonzero vectors, then (f|g) = 0."
Step by Step Solution
There are 3 Steps involved in it
Step: 1
To solve this question we need to analyze each statement to determine which four are true Lets go through each one Statement a Matrix hatA and its Inverse The statement is Matrix hatA has an inverse T...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


