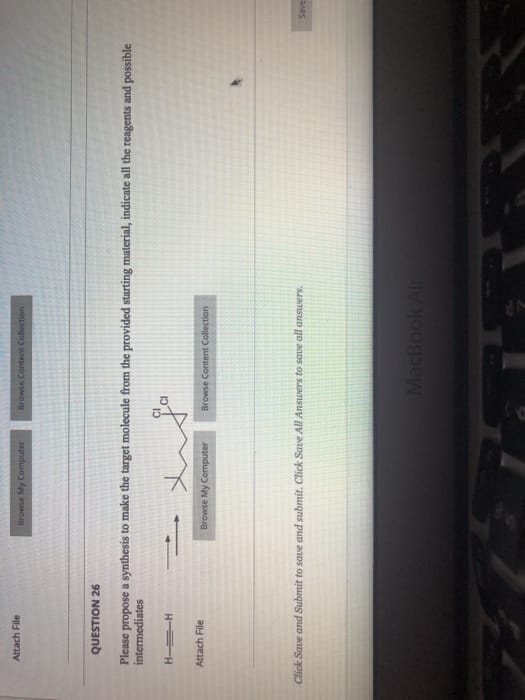
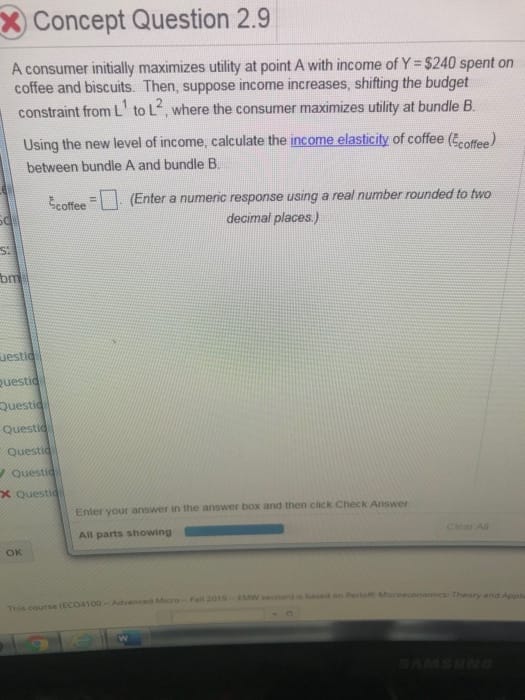
This the second time am posting this, correct answers only pls.9
4. (30 points) Consider the following game. There are ten dollars to divide. Two players are each required to simultaneously name an integer between 0 and 10. The player who names the higher number gets to keep the money. If they name the same number, the money is equally shared between them. (a) Describe the set of players /, the set of strategies {S,lien, and the payoff function fuiliEN. (b) Are there strategies that are strictly dominated? Demonstrate your reasoning. What are the resulting strategies after iterated elimination of strictly dominated strategies? (c) Find the best responses (correspondence) for each player. That is, find the strategies that maximize a player's payoff given what the other player does. (d) Find the Nash equilibria of the game. (e) Suppose now the game is changed. Whenever there is a tie, each player receives nothing. Answer the same questions in parts (b) and (c). Find the pure-strategy Nash equilibria of the game.Attach File Browse My Computer Browte Content Collection QUESTION 26 Please propose a synthesis to make the target molecule from the provided starting material, indicate all the reagents and possible intermediates H CI Attach File Browie My Computer Browse Content Collection Click Save and Submit to save and submit. Click Save All Answers to save all answers, MacBook AirA website tracks advanced exam registrations and performance by high school students. In a recent year, of the students who took the microeconomics exam, 42% passed. In an attempt to determine if the proportion of those passing the advanced math and science exams is equal to the 42% success rate for microeconomics, a random sample of 300 students enrolled in advanced math and science classes has been selected. Complete parts a and b below. a. If 46 of the students in the sample passed at least one advanced math or science exam, calculate the proportion of those students who passed at least one math or science exam. Does this statistic indicate that the proportion of students who passed at least one advanced math or science exam is less than the 42% success rate for microeconomics? Support your assertion. The proportion of those students who passed at least one math or science exam is 1. (Round to three decimal places as needed.) Does this statistic indicate that the proportion of students who passed at least one advanced math or science exam is less than the 42% success rate for microeconomics? Support your assertion. A. Yes, because the sample proportion is greater than 0.42. O B. No, because the sample proportion is greater than 0.42. O C. No, because the sample proportion is less than 0.42. O D. Yes, because the sample proportion is less than 0.42. b. Calculate a 95% confidence interval for the proportion of those students who passed at least one advanced math or science exam. The 95% confidence interval estimate is 1- -1. (Round to three decimal places as needed. Use ascending order.)X Concept Question 2.9 A consumer initially maximizes utility at point A with income of Y = $240 spent on coffee and biscuits. Then, suppose income increases, shifting the budget constraint from L' to L', where the consumer maximizes utility at bundle B. Using the new level of income, calculate the income elasticity of coffee (5coffee) between bundle A and bundle B. Scoffee =(Enter a numeric response using a real number rounded to two decimal places.) om Jestid Question Questid Questic Questid Questid x questid Enter your answer in the answer box and then click Check Answer All parts showingPrevious Pago Next Page Page 1 of 4 Question 1 (1 point) In some markets, we see firms selling products that are close substitutes, but not perfect substitutes. These are called O differentiated products O homogeneous products O inelastic products O efficient products Question 2 (1 point) Game theory Ois a qualitative approach to studying market structures O is the use of video gaming to simulate economic dynamics is a branch of microeconomics that studies sports O is a mathematical method used in microeconomics Question 3 (1 point)