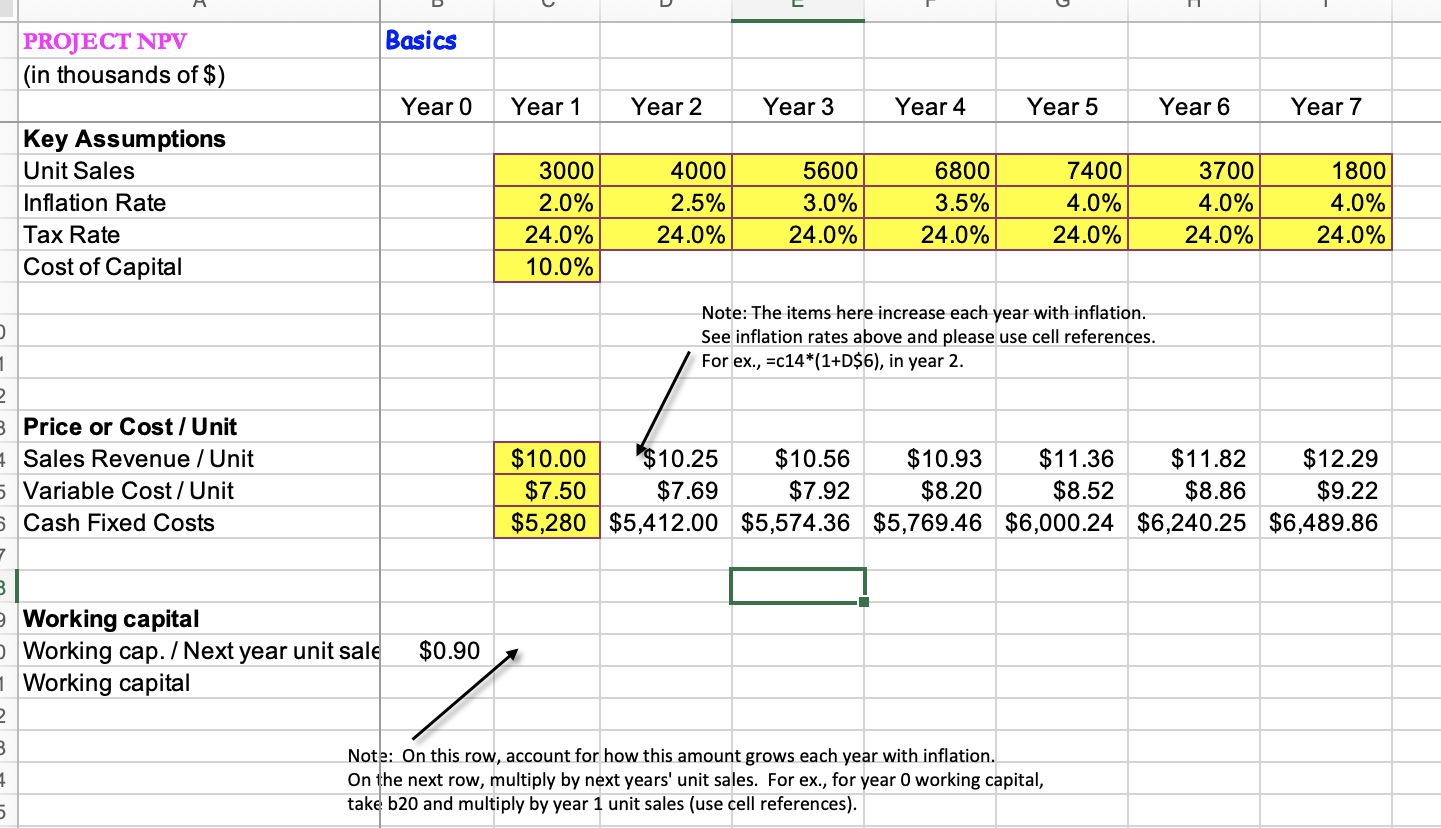
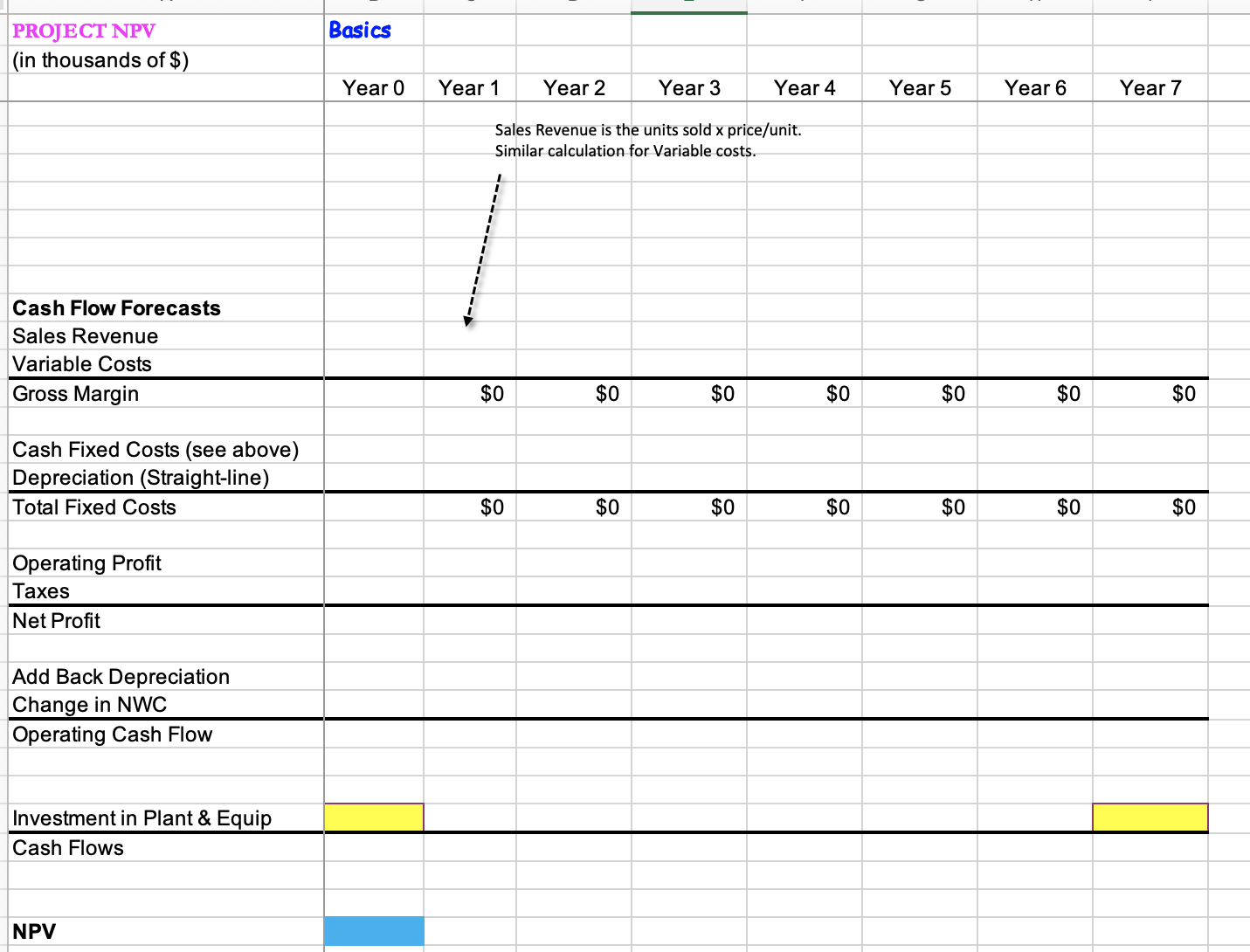thousands of dollars). In year 0 , the project requires an $11,500 investment in plant and equipment. This equipment is depreciated using the straight-line method over seven years, and has a salvage value (after-tax) of $1,200 in year 7 . The project is expected to generate sales of 3,000 units in year 1. Details on the annual unit sales are given in the spreadsheet template, highlighted in yellow. Sales revenue per unit is forecast to be $10.00 in year 1 and then grow with inflation. Variable cost per unit is forecast to be $8.00 in year 1 and then grow with inflation. Cash fixed costs are forecast to be $5,280 in year 1 and then grow with inflation. The inflation rates that apply each year (to sales, VC, and FC) are shown in the spreadsheet. The company uses a 10% discount rate to evaluate new product decisions. The tax rate is forecast to be a constant 24.0%. The project will require working capital in the amount of $0.90 in year 0 for every unit of next year's forecasted sales, and this amount ($0.90) will grow with inflation going forward. 1) What is the project's NPV? What is the IRR? Would you accept this project? 2) Suppose you need to do some sensitivity analysis (please show on separate worksheet tab): (a) What if the firm suspects that this project is riskier than the firm's average project and decides to increase the cost of capital to 13%. What is the NPV? (b) What if the firm fears that its variable costs may be higher than estimated? What if the variable cost/unit starts off at $8.40 in year 1 , and then grows with inflation - what is the NPV? (assume the original cost of capital of 10% ) \begin{tabular}{|c|c|c|c|c|c|c|c|c|} \hline & & & & & & & & \\ \hline PROJECT NPV & Basics & & & & & & & \\ \hline \multicolumn{9}{|l|}{ (in thousands of \$) } \\ \hline & Year 0 & Year 1 & Year 2 & Year 3 & Year 4 & Year 5 & Year 6 & Year 7 \\ \hline \multicolumn{9}{|l|}{ Key Assumptions } \\ \hline Unit Sales & & 3000 & 4000 & 5600 & 6800 & 7400 & 3700 & 1800 \\ \hline Inflation Rate & & 2.0% & 2.5% & 3.0% & 3.5% & 4.0% & 4.0% & 4.0% \\ \hline Tax Rate & & 24.0% & 24.0% & 24.0% & 24.0% & 24.0% & 24.0% & 24.0% \\ \hline \multirow[t]{4}{*}{ Cost of Capital } & & 10.0% & & & & & & \\ \hline & & & \multirow{2}{*}{\multicolumn{5}{|c|}{\begin{tabular}{l} Note: The items here increase each year with inflation. \\ See inflation rates above and please use cell references. \end{tabular}}} & \\ \hline & & & & & & & & \\ \hline & & & \multicolumn{3}{|c|}{ For ex., =c14(1+D$6), in year 2 . } & & & \\ \hline \multicolumn{9}{|l|}{ Price or Cost / Unit } \\ \hline Sales Revenue / Unit & & $10.00 & $10.25 & $10.56 & $10.93 & $11.36 & $11.82 & $12.29 \\ \hline Variable Cost/Unit & & $7.50 & $7.69 & $7.92 & $8.20 & $8.52 & $8.86 & $9.22 \\ \hline Cash Fixed Costs & & $5,280 & $5,412.00 & $5,574.36 & $5,769.46 & $6,000.24 & $6,240.25 & $6,489.86 \\ \hline & & & & & & & & \\ \hline \multicolumn{9}{|l|}{ Working capital } \\ \hline \multirow{2}{*}{\multicolumn{9}{|c|}{\begin{tabular}{l} Working cap./Next year unit sale \\ Working capital \end{tabular}}} \\ \hline & & & & & & & & \\ \hline \multirow{3}{*}{\multicolumn{9}{|c|}{\begin{tabular}{l} Note: On this row, account for how this amount grows each year with inflation. \\ On the next row, multiply by next years' unit sales. For ex., for year 0 working capital, \\ take b20 and multiply by year 1 unit sales (use cell references). \end{tabular}}} \\ \hline & & & & & & & & \\ \hline & & & & & & & & \\ \hline \end{tabular}