Three questions in total, easy python code please help!
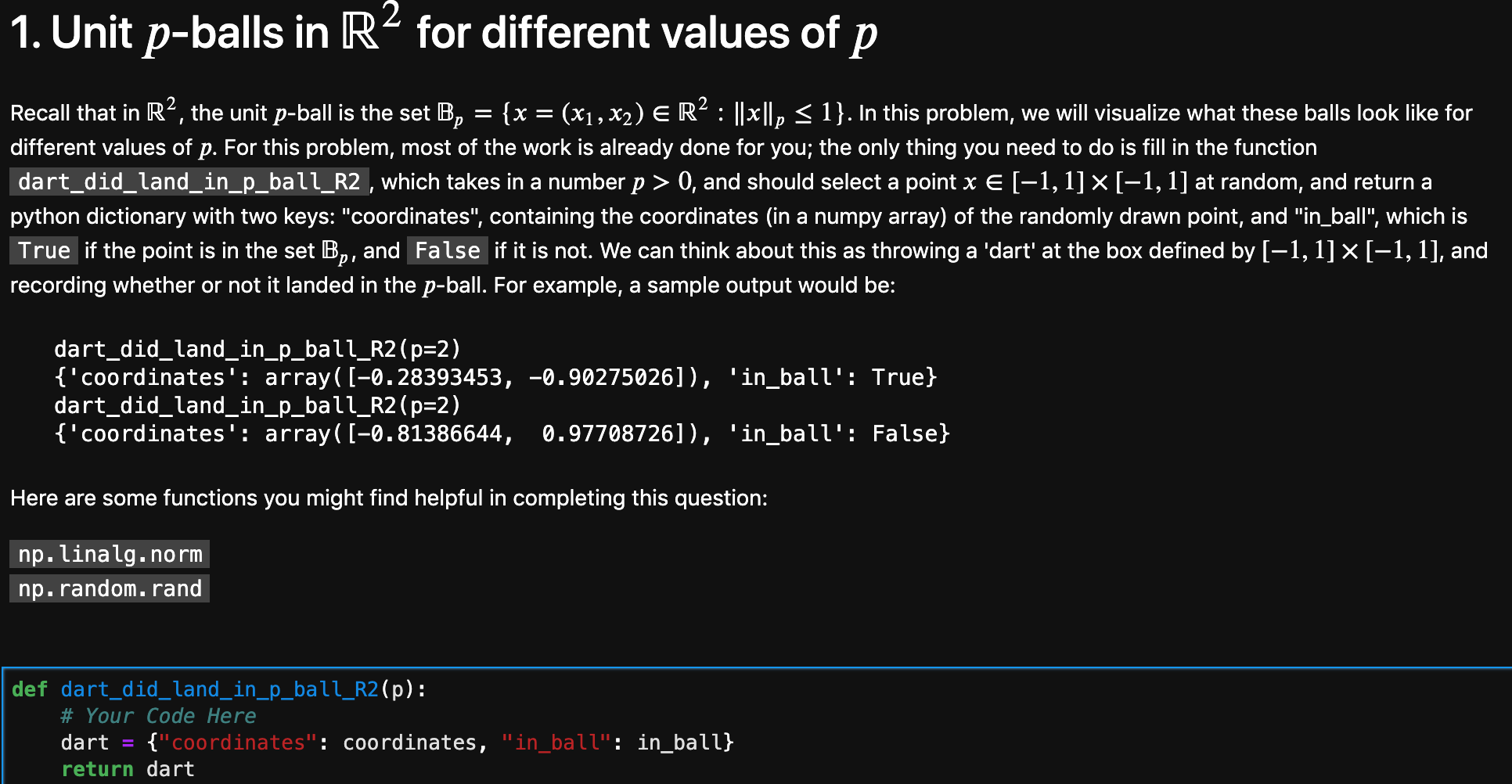

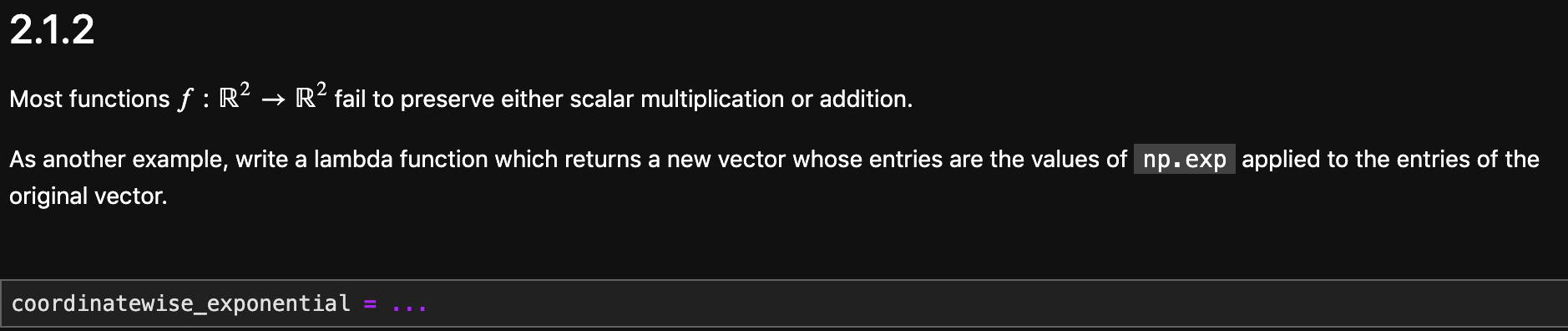
# Don't change this cell; just run it. import numpy as np import math import matplotlib.pyplot as plt from linalg_for_datasci.widgets import ( p_ball_widget, init_updating_plot, updating_ball_to_box_ratio_plot, plt.style.use("fivethirtyeight") matplotlib widget 1. Unit p-balls in R4 for different values of p Recall that in R2, the unit p-ball is the set B, = {x = (x1, x2) ER2 : ||*||, 0, and should select a point x e[-1, 1] x [-1, 1] at random, and return a python dictionary with two keys: "coordinates", containing the coordinates (in a numpy array) of the randomly drawn point, and "in_ball", which is True if the point is in the set Bp, and False if it is not. We can think about this as throwing a 'dart' at the box defined by [-1, 1] x [-1, 1), and recording whether or not it landed in the p-ball. For example, a sample output would be: dart_did_land_in_p_ball_R2 (p=2) {'coordinates': array([-0.28393453, -0.90275026]), 'in_ball': True} dart_did_land_in_p_ball_R2 (p=2) {'coordinates': array( (-0.81386644, 0.97708726]), 'in_ball': False} Here are some functions you might find helpful in completing this question: np. linalg.norm np. random. rand def dart_did_land_in_p_ball_R2(p): # Your Code Here dart = {"coordinates": coordinates, "in_ball": in_ball} return dart 2. Visualizing Linear Functions Being a linear function involves "preserving" or "commuting with" the two fundamental operations of vector spaces: addition and scalar multiplication. Specifically, if V and W are two vector spaces, then a function f:V W is linear if and only if: For any vector y EV and any real number (scalar) a ER, the function f "preserves" i.e. "commutes with" scalar multiplication: f(a. v) = a. f(v). For any two vectors vi, v, EV, the function f "preserves" i.e. "commutes with addition: f(vi + v2) = f(y) + f(v2). In the cells below, we will try to visualize the effects that certain functions f:R? R2 have on vectors, and what it looks like when they are linear, and what it looks like when they aren't. 2.1 Functions that preserve neither addition nor scalar multiplication 2.1.1 In the cell below, write a lambda function which, given as input a vector, returns a new vector whose entries are the values of np.sin applied to the entries of the original vector. coordinatewise_sin = ... 2.1.2 Most functions f:R4 R4 fail to preserve either scalar multiplication or addition. As another example, write a lambda function which returns a new vector whose entries are the values of np.exp applied to the entries of the original vector. coordinatewise_exponential =










