To define the functions (whatever is on the right-hand side of the '='), only use:

- The initial primitive recursive functions (above)

- The primitive recursive operators (above)

- Previously defined primitive recursive functions

Here is the HASKELL code:

type PN = [Char] type Vec = [PN]

-- 1) Zero function z :: Vec -> PN z x = "0"

-- 2) Successor function s :: Vec -> PN s x = ('S':(head x))

-- 3) Projection function pr :: Int -> (Vec -> PN) pr n = \x -> x !! (n-1)

-- 4) Composition circ :: (Vec -> PN) -> [(Vec -> PN)] -> (Vec -> PN) circ f gs = \x -> f $ sequence gs x

-- 5) Primitive recursion operator rho :: (Vec -> PN) -> (Vec -> PN) -> (Vec -> PN) rho f g = h where h ("0":xs) = f xs h (('S':n):xs) = g $ n:((h (n:xs)):xs)

-- 6) Addition function add = rho f_add g_add f_add = g_add =

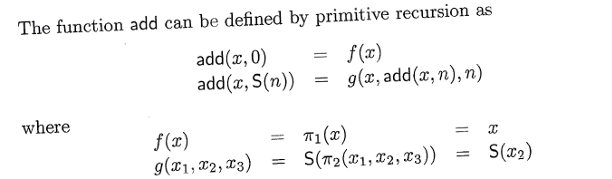
-- 7) Subtraction function

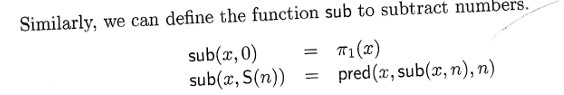
-- 8) Predecessor function

-- 9) Truncated Subtraction function

-- 10) Multipication function

-- 11) Exponent function

-- 12) Boolean Signature function

-- 13) Equality function

The function add can be defined by primitive recursion as add(x,0)add(x,S(n))=f(x)=g(x,add(x,n),n) where Similarly, we can define the function sub to subtract numbers. sub(x,0)sub(x,S(n))=1(x)=pred(x,sub(x,n),n) where the function pred is defined below predecessor (defined by primitive recursion). pred(x,y,z)predecessor(0)predecessor(S(n))=predecessor(2(x,y,z))=0=2(predecessor(n),n) The primitive recursive function mul is defined by mul(x,0)mul(x,S(n))=f(x)=g(x,mul(x,n),n) where f(x)=0g(x1,x2,x3)=add(1(x1,x2,x3),2(x1,x2,x3))=add(x1,x2) The predicates eq (equality) and It (less than) are primitive recursive with characteristic functions Xit(x,y)=f(sub(y,x))Xeq(x,y)=f(add(sub(x,y),sub(y,x))) where f(0)=0 and f(S(n))=1. The function f is primitive recursive (see the exercises at the end of the chapter)