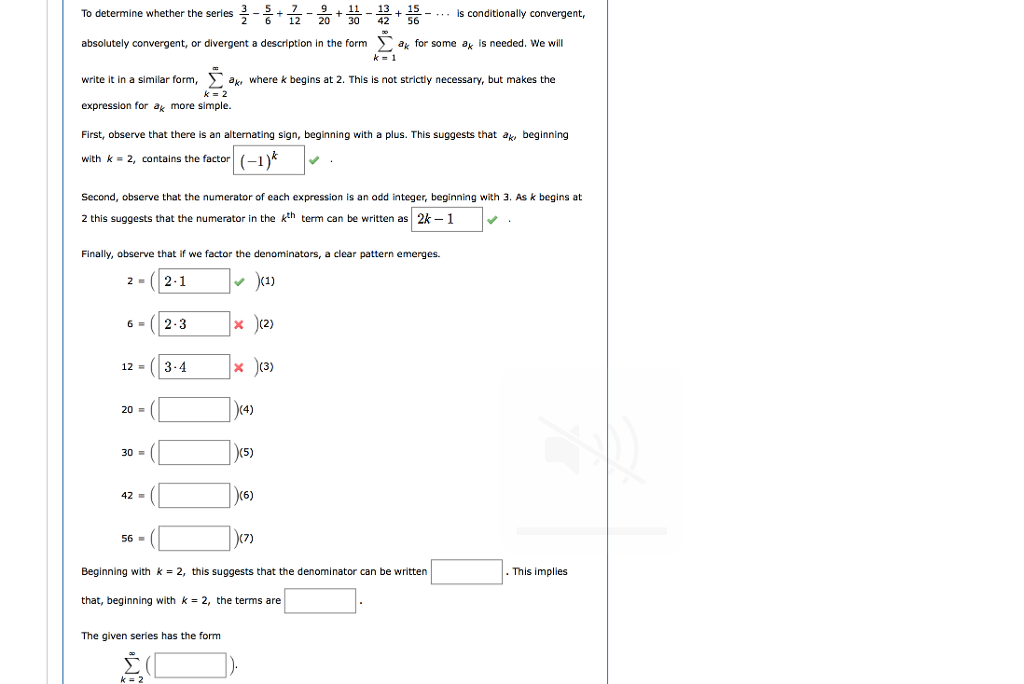
To determine whether the series absolutely convergent, or divergent a description in the form write it in a similar form, aki where k begins at 2. This is not strictly necessary, but makes the k = 2 expression for a more simple. First, observe that there is an alternating sign, beginning with a plus. This suggests that ak, beginning with k = 2, contains the factor (-1) 2 Second, observe that the numerator of each expression is an odd integer, beginning with 3. As k begins at 2 this suggests that the numerator in the th term can be written as 2k-1 Finally, observe that if we factor the denominators, a clear pattern emerges. 2.1 (1) 6 = 12 = 20 = 30 = 42 = 2 - 2 + 72-20 + 30-42 + 36 56 = 2-3 3-4 k=2 The given series has the form ( x (2) x (3) (4) (5) ak for some ak is needed. We will (6) is conditionally convergent, (7) Beginning with k = 2, this suggests that the denominator can be written that, beginning with k = 2, the terms are This implies