To find the maximum profit, note that the furthest point on the revenue curve has a slope equal to the cost. It turns out that the slope of the revenue is called the marginal revenue and is given by the equation:

= ^-bx (with the same c, a, and b as found earlier)

If you set this equal to the marginal cost (the cost per pound that was originally given to you), you can solve for x. You should be able to see that this corresponds to the point on the graph where profit is the greatest.

So, to summarize:

1. Collect the revenue data for different amounts of fertilizer and the marginal cost
2. Create three columns in Excel, the first two representing x (the number of lbs of fertilizer) and = () (the additional revenue from that much fertilizer), and the third representing the total cost C(x) of that much fertilizer. Plot an x-y scatterplot of revenue and cost as a function of the number of lbs.
3. Estimate the upper limit of the revenue c, create a fourth column for 1-y/c and graph that on a separate chart as a function of x. Add an exponential trendline with the equation and R^2 and adjust c for the best fit.
4. Use linear interpolation (intersection of the two lines connecting the points immediately before and after the break-even point) to estimate the number of pounds of fertilizer where the revenue and the cost are the same. Confirm using the formula you found for R(x) and C(x)
5. Solve = using the equation for marginal revenue above to find the number of pounds of fertilizer when profit is maximized.

My data (step 1):

0	0
250	507
500	648
750	683
1000	694
1250	698
1500	700
1750	700
2000	700

MC = 0.65

I am adding some images of the formulas used for this assignment just to simplify things for you.

Please add the work to this thank you!

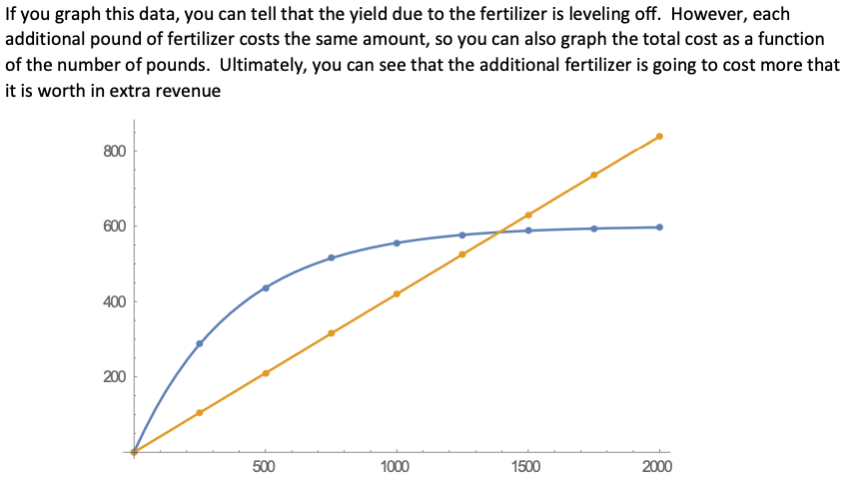
If you graph this data, you can tell that the yield due to the fertilizer is leveling off. However, each additional pound of fertilizer costs the same amount, so you can also graph the total cost as a function of the number of pounds. Ultimately, you can see that the additional fertilizer is going to cost more that it is worth in extra revenue 800 600 400 200 500 1000 1500 2000 If you graph this data, you can tell that the yield due to the fertilizer is leveling off. However, each additional pound of fertilizer costs the same amount, so you can also graph the total cost as a function of the number of pounds. Ultimately, you can see that the additional fertilizer is going to cost more that it is worth in extra revenue 800 600 400 200 500 1000 1500 2000