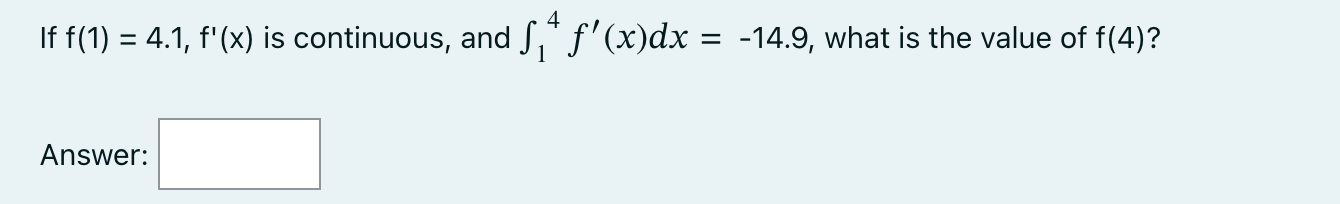
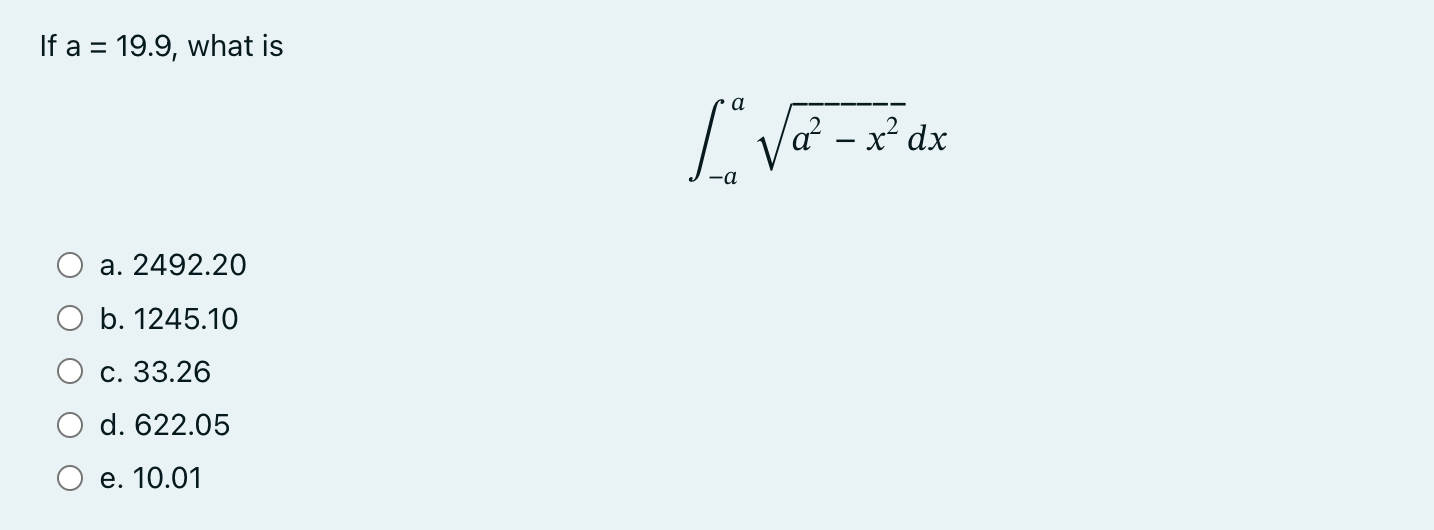
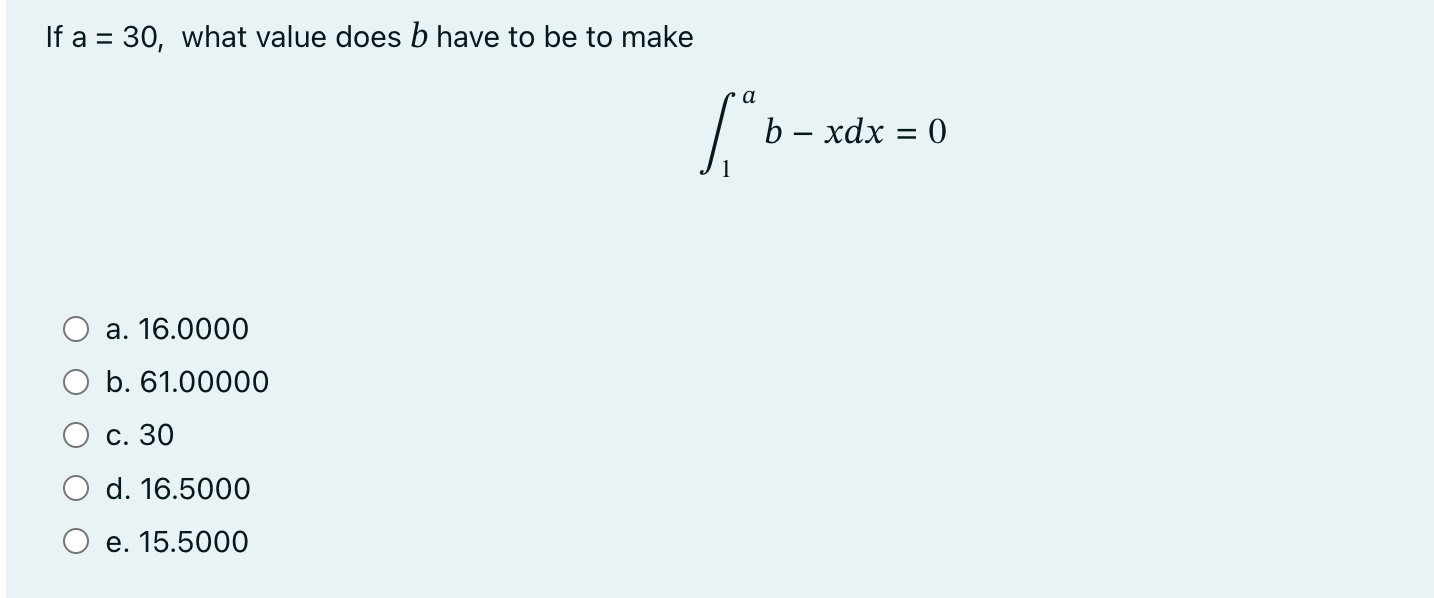
To help get in shape, Zahra gets a new pair of running shoes. If she runs 1 kilometer each day in week 1 and then adds 1/17.2 of a kilometer each week to her routine, how many kilometers has she run after 8 weeks? Round your answer to five decimal places. Answer: If n = 94, and f (x) = 84100 - x, what is the absolute difference between the left and right endpoint Riemann sums on [-290, 290]? Round your answer to 4 decimal places. Answer: When creating a Riemann sum, what is the width of an approximating rectangle on [44.1, 234.2], if we are using 14 rectangles? a. 13.58 b. 1332.70 c. 20.88 d. 1951.10 e. 741.73 When creating a left-endpoint Riemann sum on the interval [-50.6, 211.9] using 13 rectangles, the 8th endpoint used to calculate the height of the approximating rectangle would be a. 211.9 b. 111.94 c. -50.6 d. 144.35 e. 90.75 When creating a right-endpoint Riemann sum on the interval [-79.1, 479.4] using 28 rectangles, the 8th endpoint used to calculate the height of the approximating rectangle would be a. 480.7143 b. 241.0429 c. 479.4 d. 80.4714 e. -79.1 If f(1) = 4.1, f'(x) is continuous, and + f'(x)dx = -14.9, what is the value of f(4)? Answer: An icosahedron is a Platonic solid with a surface that consists of 20 equilateral triangles. By what factor does the surface area of an icosahedron increase as the side length of each triangle doubles from a unit to 2a units, if a = 16.3? Round your answer to three decimal places. Answer: As a car accelerates, it does not accelerate at a constant rate; rather, the acceleration is variable. The quadratic function a(t) = 0.70t + 1.44t + 10.44 describes the acceleration in seconds. Compute the average value of a(t) to estimate the average acceleration between t = 0 and t = 6.7 seconds. Round your answer to five decimal places. Answer: Let A be the area under y = e* and above the x-axis, on [0,a]. Let B be the area under y = ex and above the x-axis, on [0,b]. B is 10.1 times A. What is b in terms of a? a. a In(10.1e^b + 1) = b. b = In(10.1e^a + -9.1000) c. b = In(e^a + -8.10) d. b = In(10.1e^a + 10.1) e. b = In(10.1 -9.10) Suppose that for each i such that 1 i N one has i What is if N = 62? Answer: L f(t)dt = i N f(t)dt 4 4 2 Suppose that f* f(x)dx = -17.6, (x)dx = 8.4, g(x)dx = 12.6, and g(x)dx = 15.5. Then what is a. 20.90 b. -4.00 c. -24.90 d. -20.10 e. -28.90 4 [* f(x) + g(x)dx If a 19.9, what is = a L = x dx -a a. 2492.20 b. 1245.10 c. 33.26 d. 622.05 e. 10.01 If a 30, what value does b have to be to make a. 16.0000 b. 61.00000 c. 30 d. 16.5000 e. 15.5000 a b xdx = 0 Consider the parabola p(x) = 1.9x + 19.6x + 16.8. For which interval [A, B] is as large as possible? L p(x)dx A A note about the choices: for some incomprehensible reason eClass sometimes switches the position of A and B. Read each option very carefully, as your interval might be a backwards version of what eClass is showing as an option. a. [25.5537, 13.6463] b. [-1.9. 19.6] c. [0.79576, -11.11155] d. [5.1579, -5.1579] e. [5.9537, -5.9537]