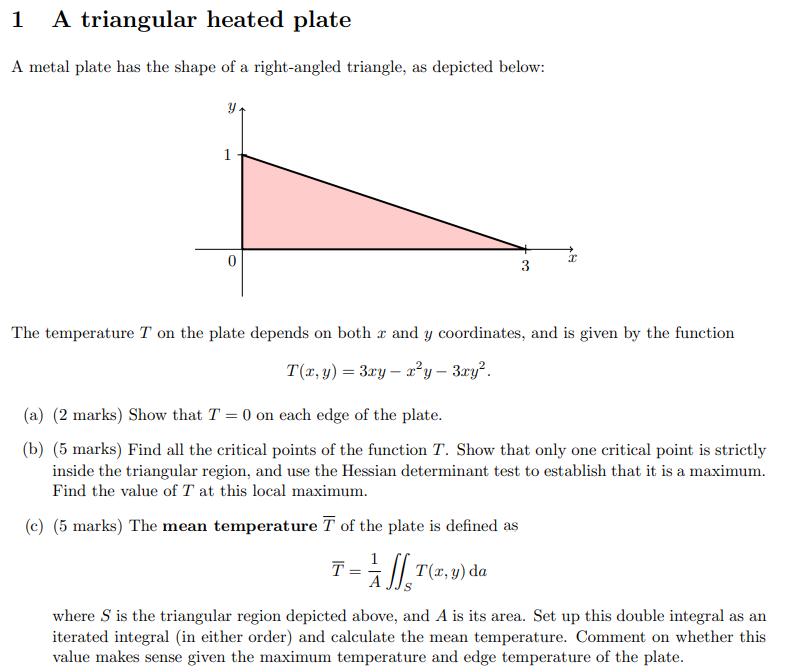
Question: A metal plate has the shape of a right-angled triangle, as depicted below: x y 3 1 0 The temperature T on the plate depends
A metal plate has the shape of a right-angled triangle, as depicted below: x y 3 1 0 The temperature T on the plate depends on both x and y coordinates, and is given by the function T(x, y) = 3xy − x^2 y − 3xy^2 .
(a) Show that T = 0 on each edge of the plate.
(b)Find all the critical points of the function T. Show that only one critical point is strictly inside the triangular region, and use the Hessian determinant test to establish that it is a maximum. Find the value of T at this local maximum.
(c) The mean temperature T of the plate is defined as 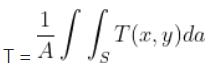 where S is the triangular region depicted above, and A is its area. Set up this double integral as an iterated integral (in either order) and calculate the mean temperature. Comment on whether this value makes sense given the maximum temperature and edge temperature of the plate.
where S is the triangular region depicted above, and A is its area. Set up this double integral as an iterated integral (in either order) and calculate the mean temperature. Comment on whether this value makes sense given the maximum temperature and edge temperature of the plate.
1 TAS S T(x, y) da T =
Step by Step Solution
3.36 Rating (159 Votes )
There are 3 Steps involved in it
AL At Ist Edges 2nd Ediges you 3ral Edge Y 01 X O 5 Now 3 11 O Tx 0 3x 0 x 0 Ju 0 0 y o ... View full answer

Get step-by-step solutions from verified subject matter experts


