TODO: Generate Figure 4.6 from Alpaydin 4th Edition: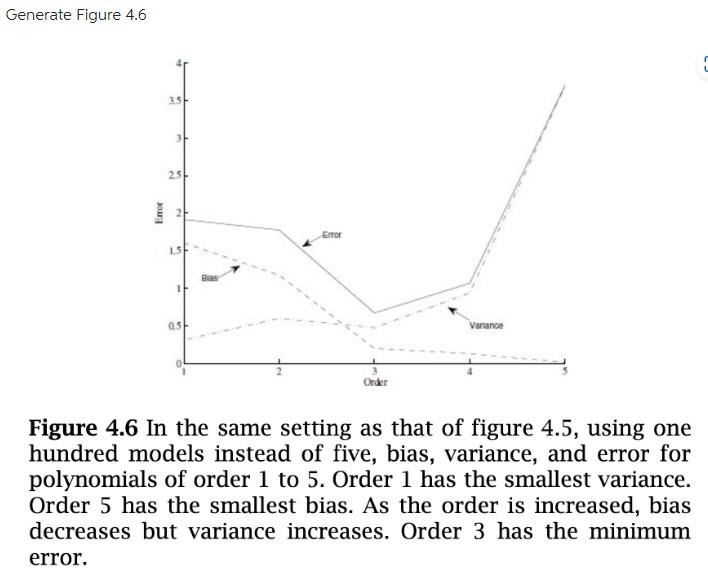

The x-axis is the order of polynomial model, from 1 to 5. the y-axis is the error. The plot should contain three curves: total error, bias error and variance error.

Use all 100 dataset to compute the total error, bias error and variance error functions by using total error equation (4.36):

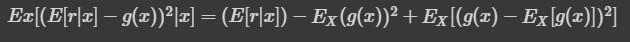
Evaluate each of the three error functions with 10 equally spaced values starting from 0 and ending at 5, i.e. np.linspace(0, 5, 10)

TODO: For each of the five polynomial models, print the average predictions, EX[g(x)], at np.linspace(0, 5, 10)

Hint: Average prediction at point x means computing the average value of the predictions of 100 models generated by 100 datasets. The point x should range from np.linspace(0, 5, 10)

TODO: Generate and print a DataFrame with 5 rows, one for each order and 4 columns. The 4 columns are:

Order

Bias error

Variance error

Total error

Hint: Average prediction at point x means computing the average value of the predictions of 100 models generated by 100 datasets. The point x should range from np.linspace(0, 5, 10)

Hint: For bias error (E[r|x])EX(g(x))2, E[r|x]=f(x) and EX[g(x)] is the average over 100 models from the 100 datasets. Then, you can approximate bias error by average over x in np.linspace(0, 5, 10) of (E[r|x]EX[g(x)])2.

Hint: For For variance error, you need to have a nested loops (for each dataset and for x in np.linespace(0, 5, 10)) to get the average variance error.

Hint: The total error is the sum of bias error and variance error.

## Insert your code BEGIN

# Define any variables or methods that you need here

## Insert your code END

def bias_error(avg_pred, x_eval):

# For each polynomial order, computes its bias error

# returns a list of length 5

five_bias = []

## Insert your code BEGI

## Insert your code END

return five_bias

def variance_error(avg_pred, models_evals):

# For each polynomial order, computes its variance error

# returns a list of length 5

five_variance = []

## Insert your code BEGIN

## Insert your code END

return five_variance

# Fit 5 * 100 models, i.e. fit 100 models for each degree in range(1, 6).

# The shape of models_list is (5, 100)

models_list = []

## Insert your code BEGIN

## Insert your code END

# create evaluation x data

x_eval = np.linspace(0, 5, 10)

# Evaluate each of the 5 * 100 models on `x_eval`

# The shape of models_evals_list is (5,100,10) which is 5 degree with 100 models and each model predict the 10 x evaluation

models_evals_list = []

## Insert your code BEGIN

## Insert your code END

# For each degree compute the average predictiona at `x_eval`

# The shape `ave_preds_list` isis (5,10)

avg_preds_list = []

## Insert your code BEGIN

## Insert your code END

bias_lst = bias_error(avg_preds_list, x_eval)

variance_lst = variance_error(avg_preds_list, models_evals_list)

total_error = [x + y for x, y in zip(bias_lst, variance_lst)]

# show the plot

x_points = [1,2,3,4,5]

plt.plot(x_points, bias_lst, linestyle='dashed',label = "Bias^2", marker='o', markersize=10)

plt.plot(x_points, variance_lst, linestyle='dashed', label = "Variance", marker='o', markersize=10)

plt.plot(x_points, total_error, linestyle='solid', label = "Error", marker='o', markersize=10)

plt.legend()

plt.xlim(0.9, 5.1)

plt.xticks(np.linspace(1, 5, 5))

plt.xlabel("Order")

plt.ylabel("Error")

plt.title("Bias and Variance Trade-off")

# Display graph

plt.show()

Generate Figure 4.6 Figure 4.6 In the same setting as that of figure 4.5, using one hundred models instead of five, bias, variance, and error for polynomials of order 1 to 5 . Order 1 has the smallest variance. Order 5 has the smallest bias. As the order is increased, bias decreases but variance increases. Order 3 has the minimum error. Ex[(E[rx]g(x))2x]=(E[rx])EX(g(x))2+EX[(g(x)EX[g(x)])2]