Topic - Mathematics Optimization Problem(Linear Programming)

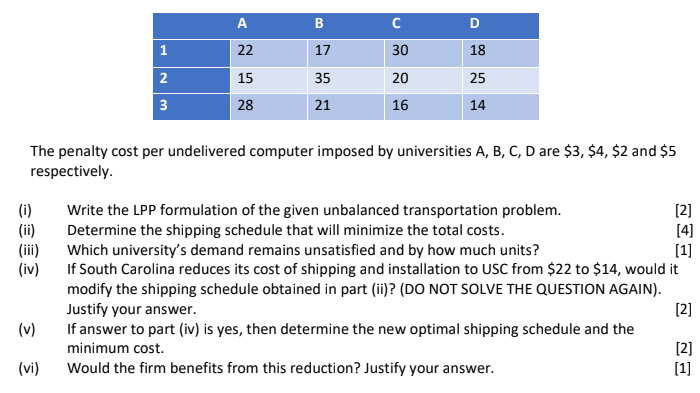
A computer brand sells personal computers to universities and ships them from three distribution warehouses. The firm is able to supply the following numbers of computers to universities by the beginning of the academic year.

Four universities have ordered computers that must be delivered and installed by the beginning of the academic year.

The shipping and installation costs (in $) per computer from each distributor (1, 2, 3) to each university (A, B, C, D) are as follows. However, Asbury University will not accept computers from warehouse at Virginia.

Distribution Warehouse Supply (computers) 1. South Carolina 2. Kentucky 3. Virginia 420 610 340 University Demand (computers) A. USC B. Asbury C. State D. Central 560 280 410 340 A | 22 | 15 28 30 20 | 16 17 35 21 2 3 18 25 14 The penalty cost per undelivered computer imposed by universities A, B, C, D are $3, $4, $2 and $5 respectively. (i) (iii) (iv) Write the LPP formulation of the given unbalanced transportation problem. Determine the shipping schedule that will minimize the total costs. [4] Which university's demand remains unsatisfied and by how much units? [1] If South Carolina reduces its cost of shipping and installation to USC from $22 to $14, would it modify the shipping schedule obtained in part (ii)? (DO NOT SOLVE THE QUESTION AGAIN). Justify your answer. If answer to part (iv) is yes, then determine the new optimal shipping schedule and the minimum cost. Would the firm benefits from this reduction? Justify your answer. (vi) Distribution Warehouse Supply (computers) 1. South Carolina 2. Kentucky 3. Virginia 420 610 340 University Demand (computers) A. USC B. Asbury C. State D. Central 560 280 410 340 A | 22 | 15 28 30 20 | 16 17 35 21 2 3 18 25 14 The penalty cost per undelivered computer imposed by universities A, B, C, D are $3, $4, $2 and $5 respectively. (i) (iii) (iv) Write the LPP formulation of the given unbalanced transportation problem. Determine the shipping schedule that will minimize the total costs. [4] Which university's demand remains unsatisfied and by how much units? [1] If South Carolina reduces its cost of shipping and installation to USC from $22 to $14, would it modify the shipping schedule obtained in part (ii)? (DO NOT SOLVE THE QUESTION AGAIN). Justify your answer. If answer to part (iv) is yes, then determine the new optimal shipping schedule and the minimum cost. Would the firm benefits from this reduction? Justify your answer. (vi)