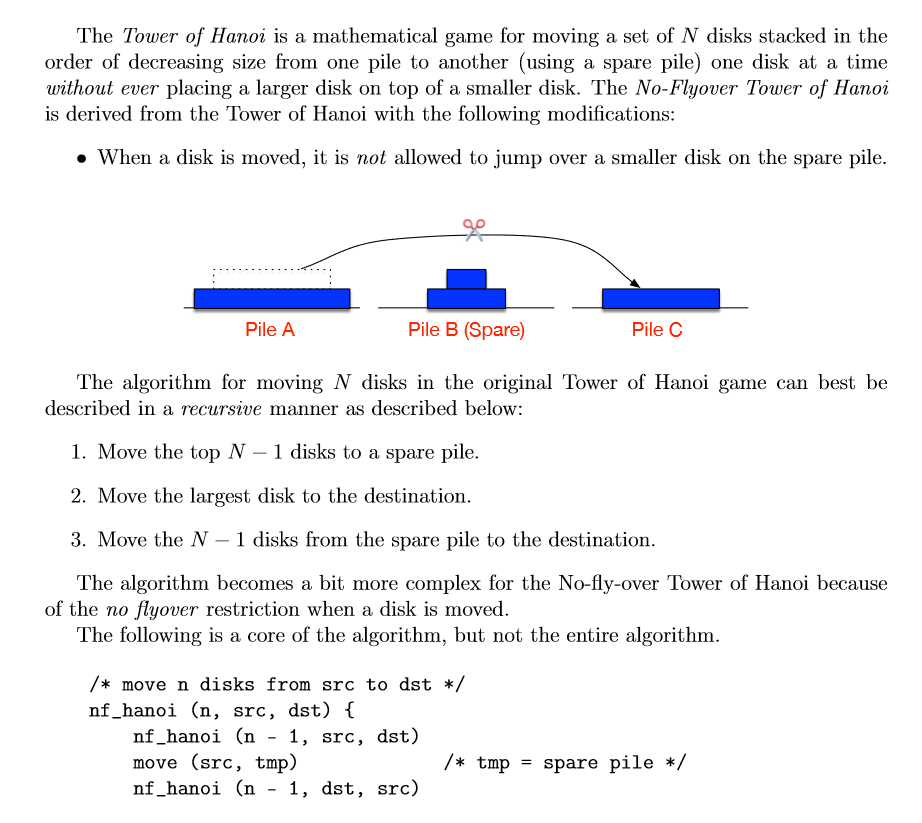
TOWER OF HANOI (NO FLY OVER)

I NEED THE ALGORITHM AND A STEP BY STEP EXPLANATION...also IF YOU CAN IMPLEMENT THIS IN A C PROGRAM THAT WOULD BE GREAT TOO... REMEMBER THIS IS A NO FLY OVER TOWER OF HANOI..

The Tower of Hanoi is a mathematical game for moving a set of N disks stacked in the order of decreasing size from one pile to another (using a spare pile) one disk at a time without ever placing a larger disk on top of a smaller disk. The No-Flyover Tower of Hanoi is derived from the Tower of Hanoi with the following modifications When a disk is moved, it is not allowed to jump over a smaller disk on the spare pile. Pile A Pile B (Spare) Pile C The algorithm for moving N disks in the original Tower of Hanoi game can best be described in a recursive manner as described below 1. Move the top N - 1 disks to a spare pile 2. Move the largest disk to the destination 3. Move the N - 1 disks from the spare pile to the destination The algorithm becomes a bit more complex for the No-fly-over Tower of Hanoi because The following is a core of the algorithm, but not the entire algorithm of the no flyover restriction when a disk is moved /move n disks from src to dst */ nf_hanoi (n, src, dst) nf_hanoi (n - 1, src, dst) move (src, tmp) nf_hanoi (n - 1, dst, src) /* tmp = spare pile */ move (NF Hanoi Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (NF Hanoi) Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (NF Hanol) Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (tmp, dst) nf_hanoi (n - 1, src, dst) The project consists of two parts: (1) to determine the minimum number of moves necessary for moving N disks from pile A to pile C; (2) to simulate the game (the details of which will be discussed in class). Note that the algorithm used for this project must be fully recursive. The number of moves it takes to complete a Tower of Hanoi game in the minimum number of steps can be calculated in a recursive manner as shown below. int hanoi (int n) if (n 1) return 1; else return 2 * hanoi(n-1) + 1 The number of moves required for a no-flyover Tower of Hanoi game would be different but can be calculated in a similar manner or directly from the simulation The Tower of Hanoi is a mathematical game for moving a set of N disks stacked in the order of decreasing size from one pile to another (using a spare pile) one disk at a time without ever placing a larger disk on top of a smaller disk. The No-Flyover Tower of Hanoi is derived from the Tower of Hanoi with the following modifications When a disk is moved, it is not allowed to jump over a smaller disk on the spare pile. Pile A Pile B (Spare) Pile C The algorithm for moving N disks in the original Tower of Hanoi game can best be described in a recursive manner as described below 1. Move the top N - 1 disks to a spare pile 2. Move the largest disk to the destination 3. Move the N - 1 disks from the spare pile to the destination The algorithm becomes a bit more complex for the No-fly-over Tower of Hanoi because The following is a core of the algorithm, but not the entire algorithm of the no flyover restriction when a disk is moved /move n disks from src to dst */ nf_hanoi (n, src, dst) nf_hanoi (n - 1, src, dst) move (src, tmp) nf_hanoi (n - 1, dst, src) /* tmp = spare pile */ move (NF Hanoi Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (NF Hanoi) Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (NF Hanol) Pile A Pile B (Spare) Pile C Pile A Pile B (Spare) Pile C move (tmp, dst) nf_hanoi (n - 1, src, dst) The project consists of two parts: (1) to determine the minimum number of moves necessary for moving N disks from pile A to pile C; (2) to simulate the game (the details of which will be discussed in class). Note that the algorithm used for this project must be fully recursive. The number of moves it takes to complete a Tower of Hanoi game in the minimum number of steps can be calculated in a recursive manner as shown below. int hanoi (int n) if (n 1) return 1; else return 2 * hanoi(n-1) + 1 The number of moves required for a no-flyover Tower of Hanoi game would be different but can be calculated in a similar manner or directly from the simulation