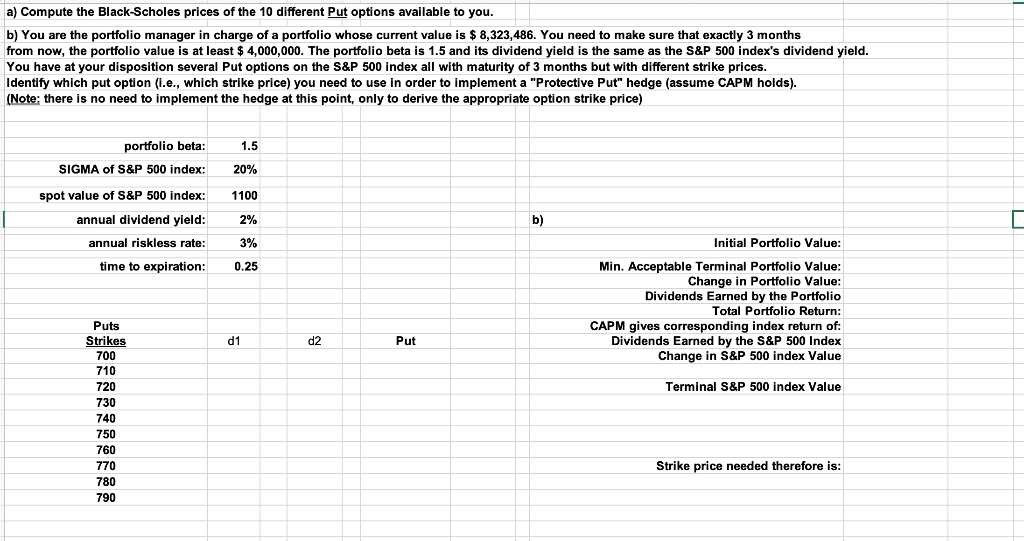
a) Compute the Black-Scholes prices of the 10 different Put options available to you. b) You are the portfolio manager in charge of a portfolio whose current value is $ 8,323,486. You need to make sure that exactly 3 months from now, the portfolio value is at least $4,000,000. The portfolio beta is 1.5 and its dividend yield is the same as the S&P 500 index's dividend yield. You have at your disposition several Put options on the S&P 500 index all with maturity of 3 months but with different strike prices. Identify which put option (i.e., which strike price) you need to use in order to implement a "Protective Put" hedge (assume CAPM holds). (Note: there is no need to implement the hedge at this point, only to derive the appropriate option strike price) portfolio beta: 1.5 SIGMA of S&P 500 index: 20% spot value of S&P 500 index: 1100 2% b) annual dividend yield: annual riskless rate: : time to expiration: 3% 0.25 Initial Portfolio Value: Min. Acceptable Terminal Portfolio Value: Change in Portfolio Value: Dividends Earned by the Portfolio Total Portfolio Return: CAPM gives corresponding index return of: Dividends Earned by the S&P 500 Index Change in S&P 500 index Value d1 d2 Put Terminal S&P 500 index Value Puts Strikes 700 710 720 72 23 730 740 ZEN 750 760 770 780 790 Strike price needed therefore is: a) Compute the Black-Scholes prices of the 10 different Put options available to you. b) You are the portfolio manager in charge of a portfolio whose current value is $ 8,323,486. You need to make sure that exactly 3 months from now, the portfolio value is at least $4,000,000. The portfolio beta is 1.5 and its dividend yield is the same as the S&P 500 index's dividend yield. You have at your disposition several Put options on the S&P 500 index all with maturity of 3 months but with different strike prices. Identify which put option (i.e., which strike price) you need to use in order to implement a "Protective Put" hedge (assume CAPM holds). (Note: there is no need to implement the hedge at this point, only to derive the appropriate option strike price) portfolio beta: 1.5 SIGMA of S&P 500 index: 20% spot value of S&P 500 index: 1100 2% b) annual dividend yield: annual riskless rate: : time to expiration: 3% 0.25 Initial Portfolio Value: Min. Acceptable Terminal Portfolio Value: Change in Portfolio Value: Dividends Earned by the Portfolio Total Portfolio Return: CAPM gives corresponding index return of: Dividends Earned by the S&P 500 Index Change in S&P 500 index Value d1 d2 Put Terminal S&P 500 index Value Puts Strikes 700 710 720 72 23 730 740 ZEN 750 760 770 780 790 Strike price needed therefore is







