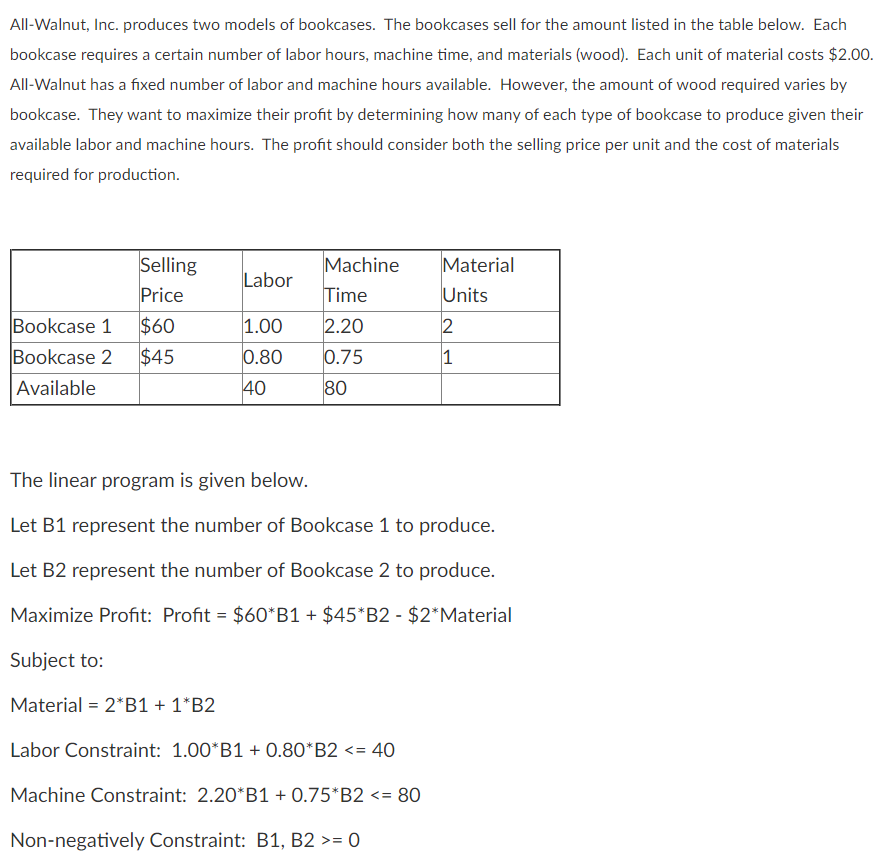
All-Walnut, Inc. produces two models of bookcases. The bookcases sell for the amount listed in the table below. Each bookcase requires a certain number of labor hours, machine time, and materials (wood). Each unit of material costs $2.00. All-Walnut has a fixed number of labor and machine hours available. However, the amount of wood required varies by bookcase. They want to maximize their profit by determining how many of each type of bookcase to produce given their available labor and machine hours. The profit should consider both the selling price per unit and the cost of materials required for production. Labor Machine Time Selling Price $60 $45 Material Units 2 1.00 2.20 Bookcase 1 Bookcase 2 Available 0.80 0.75 1 40 80 The linear program is given below. Let B1 represent the number of Bookcase 1 to produce. Let B2 represent the number of Bookcase 2 to produce. Maximize Profit: Profit = $60*B1 + $45*B2 - $2* Material Subject to: Material = 2*B1 + 1*B2 Labor Constraint: 1.00*B1 + 0.80*B2 = 0 Integer Constraint: B1, B2 Integer Create the optimization model for the problem in Excel and answer the following questions. Enter your answers as integers without dollar signs. a. How many of Bookcase 1 will you produce to maximize profit? b. How many of Bookcase 2 will you produce to maximize profti? c. What is your maximum profit? All-Walnut, Inc. produces two models of bookcases. The bookcases sell for the amount listed in the table below. Each bookcase requires a certain number of labor hours, machine time, and materials (wood). Each unit of material costs $2.00. All-Walnut has a fixed number of labor and machine hours available. However, the amount of wood required varies by bookcase. They want to maximize their profit by determining how many of each type of bookcase to produce given their available labor and machine hours. The profit should consider both the selling price per unit and the cost of materials required for production. Labor Machine Time Selling Price $60 $45 Material Units 2 1.00 2.20 Bookcase 1 Bookcase 2 Available 0.80 0.75 1 40 80 The linear program is given below. Let B1 represent the number of Bookcase 1 to produce. Let B2 represent the number of Bookcase 2 to produce. Maximize Profit: Profit = $60*B1 + $45*B2 - $2* Material Subject to: Material = 2*B1 + 1*B2 Labor Constraint: 1.00*B1 + 0.80*B2 = 0 Integer Constraint: B1, B2 Integer Create the optimization model for the problem in Excel and answer the following questions. Enter your answers as integers without dollar signs. a. How many of Bookcase 1 will you produce to maximize profit? b. How many of Bookcase 2 will you produce to maximize profti? c. What is your maximum profit