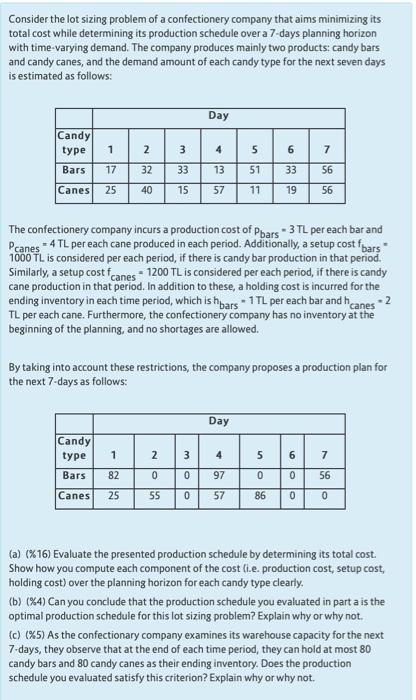
Consider the lot sizing problem of a confectionery company that aims minimizing its total cost while determining its production schedule over a 7-days planning horizon with time-varying demand. The company produces mainly two products: candy bars and candy canes, and the demand amount of each candy type for the next seven days is estimated as follows: Day Candy type 1 1 N 3 4 5 6 7 Bars 17 32 33 51 33 56 MIN Canes 25 40 15 11 19 56 The confectionery company incurs a production cost of Pbars - 3 TL per each bar and Pcanes - 4 TL per each cane produced in each period. Additionally, a setup cost fbars 1000 TL is considered per each period, if there is candy bar production in that period. Similarly, a setup cost fcanes 1200 TL is considered per each period, if there is candy cane production in that period. In addition to these, a holding cost is incurred for the ending inventory in each time period, which is hbars 1 TL per each bar and he TL per each cane. Furthermore, the confectionery company has no inventory at the beginning of the planning, and no shortages are allowed. canes 2 By taking into account these restrictions, the company proposes a production plan for the next 7-days as follows: Day Candy type 1 2 3 4 5 7 Bars 82 0 0 97 ol LOOO 56 Canes 25 55 0 57 86 0 (a) (%16) Evaluate the presented production schedule by determining its total cost. Show how you compute each component of the cost (i.e. production cost, setup cost, holding cost) over the planning horizon for each candy type clearly. (b) (%4) Can you conclude that the production schedule you evaluated in part a is the optimal production schedule for this lot sizing problem? Explain why or why not. (C) (%5) As the confectionary company examines its warehouse capacity for the next 7-days, they observe that at the end of each time period, they can hold at most 80 candy bars and 80 candy canes as their ending inventory. Does the production schedule you evaluated satisfy this criterion? Explain why or why not. Consider the lot sizing problem of a confectionery company that aims minimizing its total cost while determining its production schedule over a 7-days planning horizon with time-varying demand. The company produces mainly two products: candy bars and candy canes, and the demand amount of each candy type for the next seven days is estimated as follows: Day Candy type 1 1 N 3 4 5 6 7 Bars 17 32 33 51 33 56 MIN Canes 25 40 15 11 19 56 The confectionery company incurs a production cost of Pbars - 3 TL per each bar and Pcanes - 4 TL per each cane produced in each period. Additionally, a setup cost fbars 1000 TL is considered per each period, if there is candy bar production in that period. Similarly, a setup cost fcanes 1200 TL is considered per each period, if there is candy cane production in that period. In addition to these, a holding cost is incurred for the ending inventory in each time period, which is hbars 1 TL per each bar and he TL per each cane. Furthermore, the confectionery company has no inventory at the beginning of the planning, and no shortages are allowed. canes 2 By taking into account these restrictions, the company proposes a production plan for the next 7-days as follows: Day Candy type 1 2 3 4 5 7 Bars 82 0 0 97 ol LOOO 56 Canes 25 55 0 57 86 0 (a) (%16) Evaluate the presented production schedule by determining its total cost. Show how you compute each component of the cost (i.e. production cost, setup cost, holding cost) over the planning horizon for each candy type clearly. (b) (%4) Can you conclude that the production schedule you evaluated in part a is the optimal production schedule for this lot sizing problem? Explain why or why not. (C) (%5) As the confectionary company examines its warehouse capacity for the next 7-days, they observe that at the end of each time period, they can hold at most 80 candy bars and 80 candy canes as their ending inventory. Does the production schedule you evaluated satisfy this criterion? Explain why or why not