Transition Probability matrix
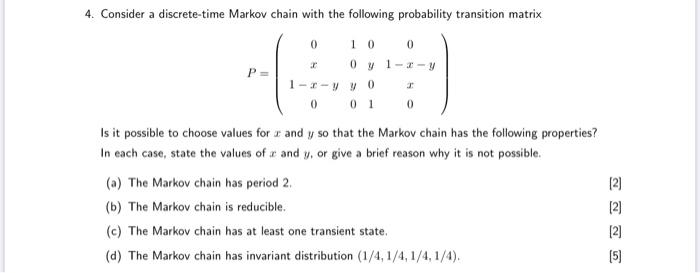
A Markov chain with state space {1, 2, 3} has transition probability matrix 0.6 0.3 0.1\\ P. = 0.3 0.3 0.4 0.4 0.1 0.5 (a) Is this Markov chain irreducible? Is the Markov chain recurrent or transient? Explain your answers. (b) What is the period of state 1? Hence deduce the period of the remaining states. Does this Markov chain have a limiting distribution? (c) Consider a general three-state Markov chain with transition matrix P11 P12 P13 P = P21 P22 P23 P31 P32 P33 Give an example of a specific set of probabilities p;; for which the Markov chain is not irreducible (there is no single right answer to this, of course !).4. Consider a discrete-time Markov chain with the following probability transition matrix 0 0 0 0 7 1-3-y P = 1-I-VVO T 0 0 1 0 Is it possible to choose values for a and y so that the Markov chain has the following properties? In each case, state the values of a and y, or give a brief reason why it is not possible. (a) The Markov chain has period 2. [2) (b) The Markov chain is reducible. (c) The Markov chain has at least one transient state. UNN (d) The Markov chain has invariant distribution (1/4, 1/4, 1/4, 1/4).1. (a) Explain what is meant by the transition probability matrix of a homogeneous Markov chain. [5 marks] (b) Explain what is meant by the stationary distribution of a Markov chain? [5 marks] (c) A Markov chain has transition probability matrix, A, with entries Ouj; and stationary distribution . Write down an expression for the entries of the reverse Markov chain. [5 marks (d) Consider the following transition probability matrix of a homogo- neous Markov chain, with three states i,j and k (the TPM is in that order). If the stationary vector of the chain is (1/9, 2/9, 2/3), determine whether the Markov chain is reversible. 1 /0.2 0.2 0.6 0.1 0.6 0.3 4 \\0.1 0.1 0.8 [5 marks] (e) Let X1, X2, Xa be a sequence of random variables resulting from the above Markov chain. If X1 = i and Xs = j what is the probability that X2 = k? [5 marks]Consider a standard chessboard with an 8 x 8 grid of possible locations. We define a Markov chain by randomly moving a single chess piece on this board. The initial location Xo is sampled uniformly among the 82 = 64 squares. At time t, the piece then chooses Xt+1 by sampling uniformly from the set of legal moves given its current location Xt. For a description of legal chess moves, see: http://en. wikipedia. org/wiki/Rules_of_chess#Basic_moves. a) Suppose the chess piece is a king, which can move to any of the 8 adjacent squares. Is the Markov chain irreducible? Is the Markov chain aperiodic? b) Suppose the chess piece is a bishop. Is the Markov chain irreducible? Is the Markov chain aperiodic? c) Suppose the chess piece is a knight. Is the Markov chain irreducible? Is the Markov chain aperiodic