Trying to solve the 8-puzzle problem , Use the Hill Climbing algorithm with random restarts and defines h2 (Manhattan distance)as heuristic function ? i need implementation of this problem in C/C++..... information about h2 (the sum of the Manhattan distances of the misplaced tiles)

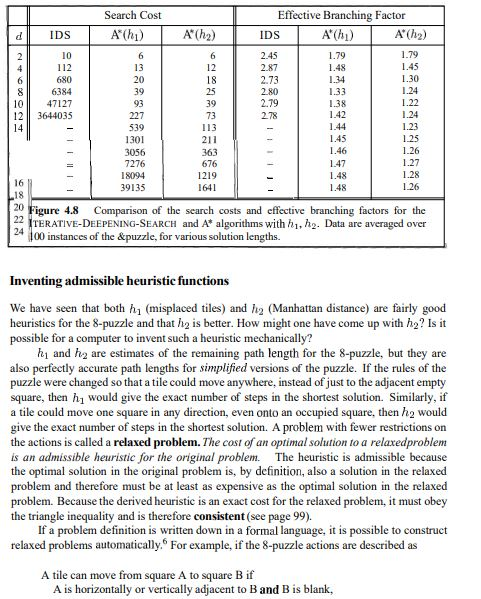
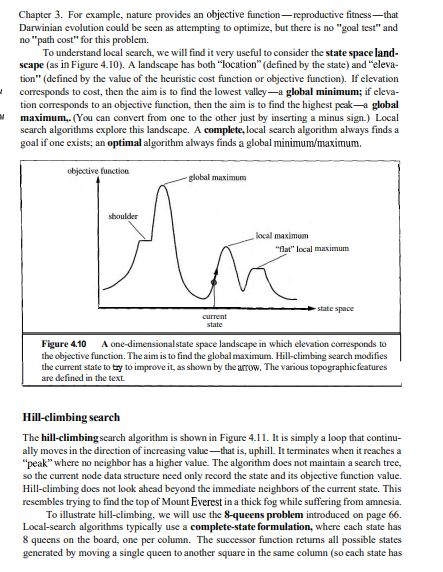
and here is some information to help to solve that problem ...... 

4.2 HEURISTIC FUNCTIONS In this section, we will look at heuristics for the 8-puzzle, in order to shed light on the nature of heuristics in general. The 8-puzzle was one of the earliest heuristic search problems. As mentioned in Sec- tion 3.2, the object of the puzzle is to slide the tiles horizontally or vertically into the empty space until the configuration matches the goal configuration (Figure 4.7). 2 5 5 3 4 3 8. Goal State Start State A typical instance of the 8-puzzle. The solution is 26 steps long. Figure 4.7 The average solution cost for a randomly generated %-puzzlanstance is about 22 steps. The branching factor is about 3. (When the empty tile is in the middle, there are four possible moves; when it is in a corner there are two; and when it is along an edge there are three.) This means that an exhaustive search to depth 22 would look at about 322 3.1 x 1010 states. By keeping track of repeated states, we could cut this down by a factor of about 170,000, because there are only 9!/2 = 181,440 distinct states that are reachable. (See Exercise 3.4.) This is a manageable number, but the corresponding number for the 15-puzzle is roughly 1013, sc the next order of business is to find a good heuristic function. If we want to find the shortest solutions by using A, we need a heuristic function that never overestimates the number of steps to the goal. There is a long history of such heuristics for the 15-puzzle; here are two commonly-used candidates: h = the number of misplaced tiles. For Figure 4.7, all of the eight tiles are out of position, so the start state would have h1 = 8. h is an admissible heuristic, because it is clear that any tile that is out of place must be moved at least once. h2 = the sum of the distances of the tiles from their goal positions. Because tiles cannot move along diagonals, the distance we will count is the sum of the horizontal and vertical distances. This is sometimes called the city block distance or Manhattan distance. ha is also admissible, because all any move can do is move one tile one step closer to the goal. Tiles I to 8 in the start state give a Manhattan distance of h2 = 3+1+2+2+2+3+3+2 = 18. The effect of heuristic accuracy on performance One way to characterize the quality of a heuristic is the effective branching factor b*. If the total number of nodes generated by A* for a particular problem is N, and the solution depth is d, then b* is the branching factor that a uniform tree of depth d would have to have in order to contain N+ / nodes. Thus, N+1 = 1+b+(b)2+..+ (6)4. For example, if A* finds a solution at depth 5 using 52 nodes, then the effective branching factor is 1.92. The effective branching factor can vary across problem instances, but usually it is fairly constant for sufficiently hard problems. Therefore, experimental measurements of b* on a small set of problems can provide a good guide to the heuristic's overall usefulness. A well-designed heuristic would have a value of b* close to 1, allowing fairly large problems to be solved. To test the heuristic functions hi and h2, we generated 1200 random problems with solution lengths from 2 to 24 (100 for each even number) and solved them with iterative deepening search and with A* tree search using both h1 and ha. Figure 4.8 gives the average number of nodes generated by each strategy and the effective branching factor. The results suggest that h is better than h1, and is far better than using iterative deepening search. On our solutions with length 14, A* with ha is 30,000 times more efficient than uninformed iterative deepening search. One might ask whether h2 is always better than h1. The answer is yes. It is easy to see from the definitions of the two heuristics that, for any node n, h2(n) 2 h1(n). We thus say that h2 dominates h1. Domination translates directly into efficiency: A* using hz will never expand more nodes than A* using h1 (except possibly for some nodes with f(n)=C*). The argument is simple. Recall the observation on page 100 that every node with f (n)