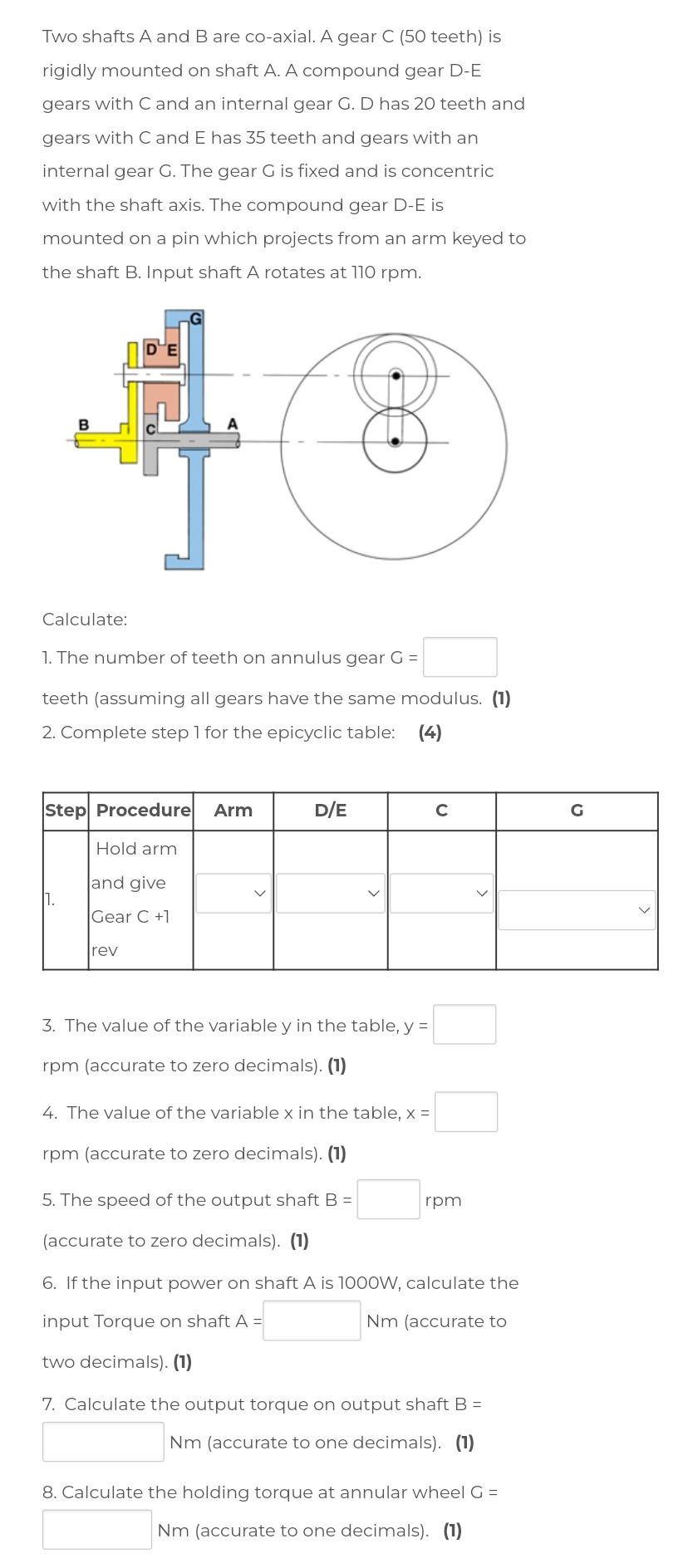
Two shafts A and B are co-axial. A gear C (50 teeth) is rigidly mounted on shaft A. A compound gear D-E gears with C and an internal gear G. D has 20 teeth and gears with C and E has 35 teeth and gears with an internal gear G. The gear G is fixed and is concentric with the shaft axis. The compound gear D-E is mounted on a pin which projects from an arm keyed to the shaft B. Input shaft A rotates at 110 rpm. B B Calculate: 1. The number of teeth on annulus gear G = teeth (assuming all gears have the same modulus. (1) 2. Complete step 1 for the epicyclic table: (4) Step Procedure Arm 1. Hold arm and give Gear C +1 rev D/E 3. The value of the variable y in the table, y = rpm (accurate to zero decimals). (1) 4. The value of the variable x in the table, x = rpm (accurate to zero decimals). (1) 5. The speed of the output shaft B = (accurate to zero decimals). (1) 6. If the input power on shaft A is 1000W, calculate the input Torque on shaft A = Nm (accurate to two decimals). (1) rpm 7. Calculate the output torque on output shaft B = Nm (accurate to one decimals). (1) 8. Calculate the holding torque at annular wheel G = Nm (accurate to one decimals). (1) G